数值分析——非线性方程与方程组的数值解法之迭代法
非线性方程与方程组的数值解法——迭代法
就是对搜索到的根进一步进行精细化处理
迭代法就是通过递推公式，产生一个序列，证明这个序列是收敛的，也就是序列的极限是存在是，并且极限值等于该方程的根
假设一个方程：
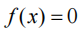
在[a,b]内有一个根x*，这个方程也可以写成：
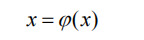
任意取x0 ∈[a,b]，计算下式是否成立:
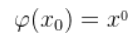
如果相等，则x0是方程的解，如果不等，x0不是方程的解，此时就令新的值为x1，如图：
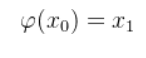
再继续计算下面的式子是否成立，
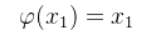
如果两者相等，则x1就是方程的根，如果不等，就令新的值为x2，如下图：
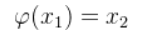
依次类推就可以得到递推公式（也称为迭代格式），如下图所示：
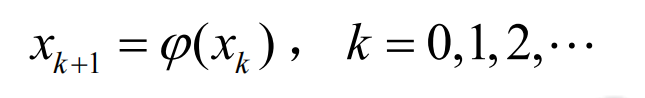
再通过这个递推公式就可以得到一个递推序列（也称为迭代序列）：
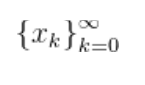
k是从0 到♾️。假设k趋向于♾️时，这个数列有极限，且极限值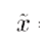 
属于区间[a,b]，
（注释：因为是闭区间，这个数列也是属于闭区间，可以根据实数的完备性理论得到，所以数列的极限值也在这个闭区间里）
并且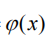
是连续的，（也称这个函数叫迭代函数），因此就可以得到极限值等于函数值，就有：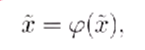
因此就可以得到：
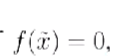
也就是会有：
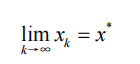
也即有：x*是方程的根
此时称迭代法收敛，否则就称迭代法发散
（也就是递推序列在k趋向于♾️时极限值没有，或者极限值不存在就是迭代法发散）。
结论
如果任意取x0 ∈[a,b]，使得迭代序列收敛，那么就称迭代格式收敛，否则就称迭代格式发散。
称ek = x*- xk是第k次的迭代误差
用迭代格式求方程的近似根的方法就叫做简单迭代法，也简称为迭代法
（也可以直接理解为：用迭代公式求方程近似根的方法就是迭代法）
当有下面式子成立时：
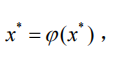
就称x*是迭代函数的不动点，故又将迭代法称其为不动点迭代法。
注意啦！！！同一个方程，选取的迭代函数不同，就有可能得到完全不同的结果，因此我们在选取迭代方程时，首先要考虑迭代方程的收敛性，也就是下文的内容，继续往下看吧~
迭代法的收敛性
也称为收敛性定理
在实际做题过程中，建议优先用2.5的公式（它也称为后验误差估计式，2.6被称为先验误差估计式），即使是用计算机也是这个公式优先哦~
证明过程如下图（实质就是用的零点定理，拉格朗日中值定理）：
证明思路：根的唯一性证明就是先用零点定理证明根的存在性，再用单调性证明根的唯一性就可以了，而对于收敛性的证明，它的证明方向主要就是证在k趋近于♾️时，|ek|趋近于0即可。证明公式时，先证低次方，再证高次方，用同样的方法进行类比。
有兴趣的朋友也可以看下教材上的证明过程，如下图：
发散性定理
假设方程 f(x)=0 , 它的等价形式为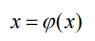
， 在区间[a,b]上有根，并且有：
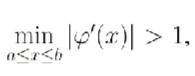
那么，对于任意的x0 ∈[a,b]，且x0 ≠ x*，则迭代格式（迭代公式）是发散的
举一个🌰
eg :
给定方程x2 + ln x -2=0，
（1）分析这个方程存在几个实根
（2）构造一个迭代格式，说明其收敛性，并用迭代求方程的根，精确到4为有效数字。
建议先自己算一下，再对照答案哦~~
解：
声明：x0就是从区间内任意取的一个数
局部收敛性
局部收敛性与收敛性的区别就在于：收敛性中对于x0的选取，在区间上任意选就可以，局部收敛性要求初始值x0必须是在精确值x*的附近选取。
局部收敛性的定义：
其实就是说，当初始值x0是接近精确值x*时，如果此时使得迭代序列收敛，那么就称为是局部收敛。
相比较而言，就是对初始值的要求提高了，对其他的条件放松了。
因为函数连续，所以导函数也连续，所以我们在计算中可以互相转换着用（导数不好算时就用函数算，反之一样。）。
局部收敛的定理：
收敛阶的定理
假设迭代公式 为：
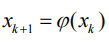
这个迭代公式收敛于方程：
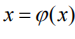的根x*，
那么，若当k —>♾️时，迭代误差ek = xk- x*满足关系式：
，
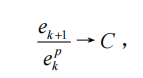其中常数C≠0，
此时，就称迭代公式是p阶收敛的，
也可以换一种角度理解就是：
假设有一个序列为：
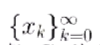
，并且这个序列收敛于x*，记 ek = x* - xk，如果存在常数 p ≥1，以及非零常数C，能够使得：
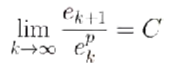
成立，那么就称这个序列是p阶收敛的。
并且有：
当 p=1 时，就称为线性收敛；
当 p=2 时，就称为平方收敛；
当 p>1 时，就称为超线性收敛。
p 的大小就反应了迭代公式收敛速度的快慢，p越大，迭代公式就收敛得越快，p越小，就收敛得越慢。
收敛阶的又又一个定理：
定理证明过程如下：
收敛阶的判别
对于迭代公式 ：
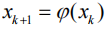
以及正整数p，如果有：
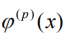
在所求的根的x的邻域内连续，并且有：
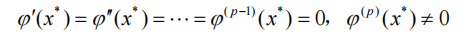
则，称这个迭代公式在点x的邻域内是p阶收敛的。
也可以换一种角度理解就是：
如果迭代公式为：
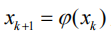
由此产生的迭代序列为：
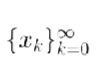
如果此时这个迭代序列是p阶收敛的，那么就称这个迭代公式是p阶收敛的。
正在努力更新中ing·······
：）