讲点芯片验证中的统计覆盖率
统计覆盖率(Statistical coverage, SCOV)应该是Arm公司提出来的一种方法,它是一种利用统计可视化从回归中提出和分析激励质量的方法。SCOV可以深入挖掘激励数据,以工程师易于理解的方式提取和呈现被统计事件的信息,并有明确的改进方向。
我前几年就接触了SCOV的一些实现,但一直都不是很重视它,也没有深入思考它的潜在价值。所以我大部分情况下可能只是应付任务的方式,实现一些激励或DUT的统计事件,在跑完验证回归后,也没有仔细去分析这些统计事件的数值背后隐含的逻辑关系和可能提升激励质量的方向。
最近这一个月,在复现一个bug的过程中,我算是真正见识到SCOV的威力。当时要复现这个bug涉及到的随机激励约束太多,方向太多,刚开始是凭经验去调整约束,然后回归看是否可以复现。经过多轮尝试,浪费了些时间,仍然毫无进展。我的领导就抓取了bug出现场景的一些关键特征作为统计事件,然后调整激励组合,看在哪一种情况下,统计事件的值更大,那么就说明该激励组合下复现bug的可能性越高。果不其然,根据回归SCOV结果,在极短的时间内就找出比较合适的激励组合,而且也复现出bug了。
经过此役,我打算以后每个项目一定要深入思考和实现一些有价值的统计事件,并经常从回归收集的SCOV结果中去分析和优化激励。SCOV像其它统计方法一样,需要对统计事件要有一定的了解,才能提出有价值的改进方向。
典型的SCOV流程是由三个阶段组成的循环——数据收集、分析和激励改进。Arm提出SCOV是因为随机激励在发现难以想象漏洞上很有帮助,但它们往往效率很低,在发现错误之间运行数十亿个周期并不罕见,这表明激励花费了大部分时间来探索相同的验证状态空间。为了提高回归效率,必须增加激励的压力和唯一性。就必须搞清在这数十亿个周期中究竟发生了什么,这是一件很难的事情。FCOV可以提供对激励方案的一个大致了解,但它提供了一个相对简单化的视角。SCOV可以对事件信息进行分组和可视化,并从事件组合上提供即时反馈。而且SCOV的仿真开销通常比CCOV和FCOV低得多,允许环境更频繁地收集和分析,也可以进行更大的回归。
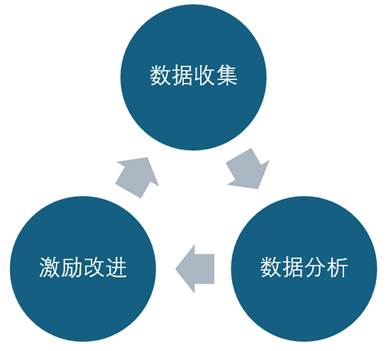
图1 典型SCOV循环流程
那么统计覆盖率是怎么实现的呢?既然统计覆盖率是由一些事件组成,并且统计这些事件发生的次数、分布情况等,就说明在验证环境中,可以定义一组计数器来代表这些事件,如果发生了A事件,那么A的计数器就加1,等所有用例仿真结束后,把所有用例中A事件的计数器值加起来,就可以得到在该次回归中,A事件发生的次数。当然,想要花样搞得多的话,可以统计一些二维或三维信息,比如随着仿真时间的变化,A事件发生的情况,然后用图表形式展示出来,这样就很直观了。也可以统计事件A和事件B之间的相关性等。
有机会可以多探索探索,收益还是很大。

