【数据结构入门】二叉树(1)
目录
1.二叉树的概念
2.特殊的二叉树
2.1 满二叉树
2.2 完全二叉树
3. 二叉树的三个公式
3.1 求K层满二叉树有多少节点
3.2 求第K层非空二叉树中最多有多少节点
3.3 度为0和度为2的结点之间的关系
4.二叉树题目
4.1 题目一
4.2 题目二
4.3 题目三
4.4 题目四
5. 推导结论
满二叉树公式:
完全二叉树公式:
满二叉树的高度:
完全二叉树的高度:
6.二叉树的数据存储
本期内容是在《树》的基础上进行的拓展,没有学习的读者,可以点击前面的跳转链接进行学习。
上一期内容讲了树,树其实本质上就是根 + 它的子树,在一棵树中的任意一个节点都满足此规律,所以树是一个递归结构。
1.二叉树的概念
就是度为2的树。每个结点最多有两个孩子,第一个孩子叫做左孩子,第二个孩子叫做右孩子。下图就是生活中真实的“二叉树”。

2.特殊的二叉树
2.1 满二叉树
一个二叉树,每一层的结点达到最大值,这个二叉树就是满二叉树,如果说这个二叉树的层数是K,那么这个结点的总数是:
2.2 完全二叉树
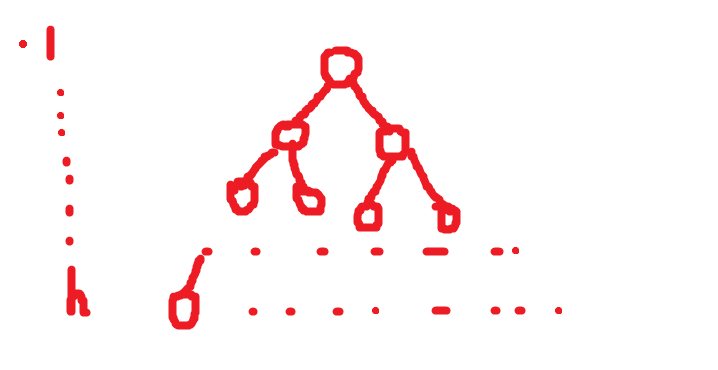
完全二叉树是一个效率很高的数据结构,完全二叉树是由满二叉树引出来的,对于深度为K的,有N个节点的二叉树,当前晋档每一个节点都与深度为K的满二叉树中编号从1到N的结点一一对应时,称之为完全二叉树,满二叉树是一种特殊的完全二叉树。
说人话就是前K-1层必须是满二叉树,最后一层可以不满,但是最后一层的结点必须是从左到右连续存放的。
下面这张图就是讲过的概念的包含顺序,其中树的概念最大。

3. 二叉树的三个公式
根结点所在的层数是1;
3.1 求K层满二叉树有多少节点
3.2 求第K层非空二叉树中最多有多少节点
3.3 度为0和度为2的结点之间的关系
度为0其实就是叶子结点,度为2就是既有左孩子还有右孩子的节点。
4.二叉树题目
4.1 题目一

叶子结点的数目 = 度为2的结点数目 + 1 = 199 + 1 = 200
选B
4.2 题目二

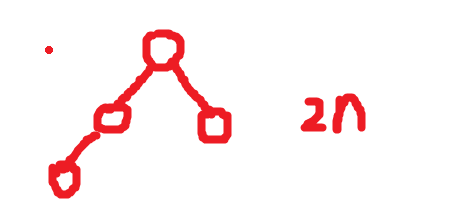
设叶子节点个数为N0,度为2的节点的个数是N2,度为1的节点的个数是N1,有N0 = N2 + 1、
N1 + N2 + N0 = 2n;带入得2N0 - 1 + N1 = 2n,化简2N0 + N1 = 2n + 1,因为是2n个节点(偶数个),说明一定是下面这种情况:一定会存在一个节点的度是1,又因为这是完全二叉树,也就是说有且仅有一个节点度为1,N1是1,那么N0就是n,选A。
4.3 题目三

2的9次方-1 = 511,说明9层满二叉树的节点个数是511,而531比9层满二叉树节点个数还要多,说明至少是10层,2的10次方-1 = 1023远大于531,说明这是一个10层不满的完全二叉树。
选B
4.4 题目四
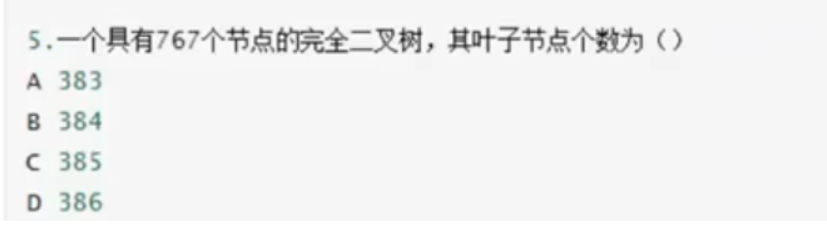
从上一题推断这是一个不满10层的二叉树,767 - 满9层二叉树511 = 256,也就是说最后一层有256个节点,占用了第9层的128个节点,第九层有2的8次方个即256个数据,被占用了128个数据,还剩128个数据没有孩子,再加上第10层原本的256个没有孩子的节点,那么就有384个叶子结点。
选B

5. 推导结论
N个节点高度是h;
满二叉树公式:
完全二叉树公式:
这里的x是最后一层可能存在的节点个数,如果X=0,那么就是满二叉树,如果是最后一层所有的节点之和,那么就会退化到上一层,所以X必须是最后一层所有结点之和-1,保证最后一层至少有一个节点。
所以X的取值范围是:
完全二叉树节点的范围:
~
满二叉树的高度:
完全二叉树的高度:
高度最小值:
将x=0带入:
高度最大值:
将x= 带入:
即:
最后:
完全二叉树高度的范围:
~
6.二叉树的数据存储
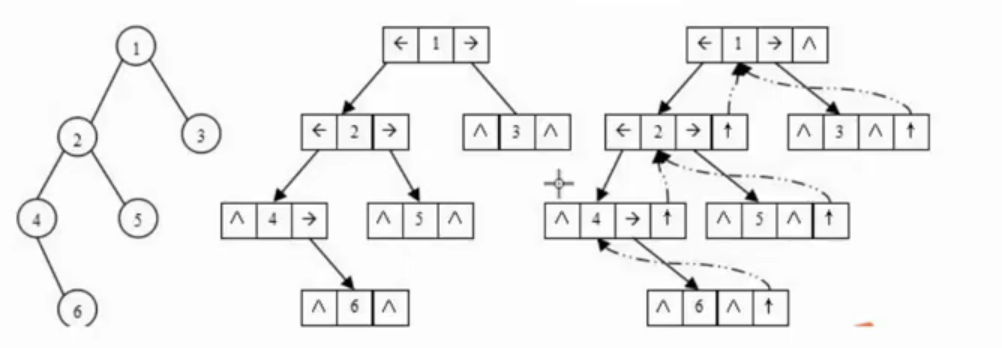
对于完全、满二叉树而言适合用数组来存储,将每一层的数据按顺序存储到数组中。
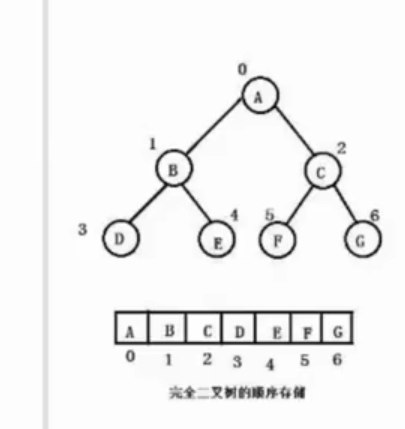
已知当前节点的下标为i,就可以求出左孩子的下标为:
求出右孩子的下标为:
已知孩子的下标为i,那么父结点的下标为:
对于非完全二叉树,使用数组存储,会有空间的浪费。
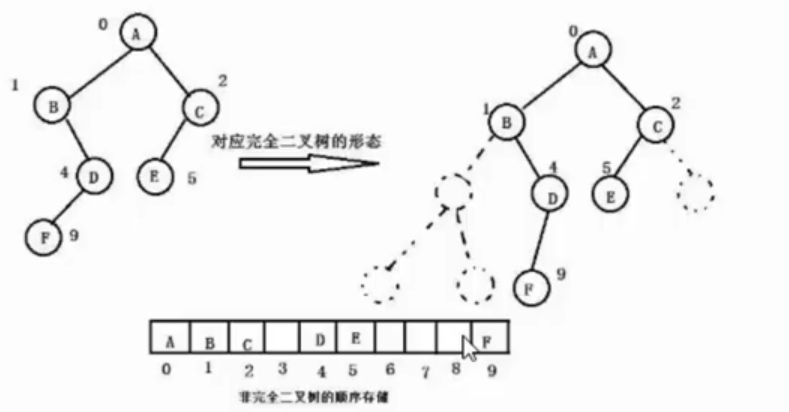
可以使用链式存储