进制定义与转换详解
文章目录
- 📘 进制定义与转换详解
- 一、进制的含义
- 二、常见进制介绍
- 1. 十进制(Decimal,Base-10)
- 2. 二进制(Binary,Base-2)
- 3. 八进制(Octal,Base-8)
- 4. 十六进制(Hexadecimal,Base-16)
- 三、进制之间的转换
- 1. 任意进制 → 十进制
- 通用公式:
- 示例:
- 2. 十进制 → 任意进制
- 方法:除基取余法(从下往上读)
- 示例:十进制 `123` → 二进制
- 示例:十进制 `100` → 八进制
- 示例:十进制 `123` → 十六进制
- 3. 二进制与其他进制的快速转换
- a. 二进制 → 八进制
- 示例:
- b. 二进制 → 十六进制
- 示例:
- 四、负数的表示(以二进制为例)
- 步骤:
- 示例:-100 的二进制表示
- 五、总结
- 进制加减法
- 进制基础与加减法运算规则
- 一、二进制(Binary)
- 二、八进制(Octal)
- 三、十进制(Decimal)
- 四、十六进制(Hexadecimal)
- 总结
- 进制对照表
📘 进制定义与转换详解
一、进制的含义
进制,也称为进位计数制,是一种人为定义的、带进位的计数方法。每种进制都有其基数(Base),表示该进制下使用的不同数字个数。
- X进制:每一位上的数字运算时都是逢X进一。
- 十进制:逢十进一
- 二进制:逢二进一
- 八进制:逢八进一
- 十六进制:逢十六进一
- ……
💡 小知识:也有不带进位的计数法,如“正”字计数、结绳记事等,但进制是现代数学和计算机中广泛使用的标准计数方式。
二、常见进制介绍
1. 十进制(Decimal,Base-10)
- 基数:10
- 符号:0 ~ 9
- 权重:10的幂次方
- 示例:
1234=1×103+2×102+3×101+4×1001234 = 1 \times 10^3 + 2 \times 10^2 + 3 \times 10^1 + 4 \times 10^0 1234=1×103+2×102+3×101+4×100
2. 二进制(Binary,Base-2)
- 基数:2
- 符号:0、1
- 权重:2的幂次方
- 用途:计算机底层表示数据的基本单位(0表示关,1表示开)
- 示例:
1002=1×22+0×21+0×20=410100_2 = 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 4_{10} 1002=1×22+0×21+0×20=410 - 表示方式:前缀
0Bint val = 0B100; // 表示十进制4
3. 八进制(Octal,Base-8)
- 基数:8
- 符号:0 ~ 7
- 权重:8的幂次方
- 用途:早期计算机系统中常用,每个八进制位对应3个二进制位
- 示例:
1238=1×82+2×81+3×80=8310123_8 = 1 \times 8^2 + 2 \times 8^1 + 3 \times 8^0 = 83_{10} 1238=1×82+2×81+3×80=8310 - 表示方式:前缀
0int val = 0123; // 表示十进制83
4. 十六进制(Hexadecimal,Base-16)
- 基数:16
- 符号:0 ~ 9 和 A ~ F(或 a ~ f),其中:
- A = 10,B = 11,C = 12,D = 13,E = 14,F = 15
- 权重:16的幂次方
- 用途:常用于内存地址、颜色编码等,每个十六进制位对应4个二进制位
- 示例:
1a2b3c16=1×165+10×164+2×163+11×162+3×161+12×160=1715004101a2b3c_{16} = 1 \times 16^5 + 10 \times 16^4 + 2 \times 16^3 + 11 \times 16^2 + 3 \times 16^1 + 12 \times 16^0 = 1715004_{10} 1a2b3c16=1×165+10×164+2×163+11×162+3×161+12×160=171500410 - 表示方式:前缀
0xint val = 0x1a2b3c; // 表示十进制1715004
三、进制之间的转换
1. 任意进制 → 十进制
通用公式:
设某进制数为 xyzw...N,其十进制值为:
Value=x×Bn−1+y×Bn−2+z×Bn−3+⋯+N×B0\text{Value} = x \times B^{n-1} + y \times B^{n-2} + z \times B^{n-3} + \cdots + N \times B^0 Value=x×Bn−1+y×Bn−2+z×Bn−3+⋯+N×B0
其中:
- $ B $:进制基数
- $ n $:数字位数
示例:
-
二进制
0B100:
1×22+0×21+0×20=41 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 4 1×22+0×21+0×20=4 -
八进制
0123:
1×82+2×81+3×80=831 \times 8^2 + 2 \times 8^1 + 3 \times 8^0 = 83 1×82+2×81+3×80=83 -
十六进制
0x1a2b3c:
1×165+10×164+2×163+11×162+3×161+12×160=17150041 \times 16^5 + 10 \times 16^4 + 2 \times 16^3 + 11 \times 16^2 + 3 \times 16^1 + 12 \times 16^0 = 1715004 1×165+10×164+2×163+11×162+3×161+12×160=1715004
2. 十进制 → 任意进制
方法:除基取余法(从下往上读)
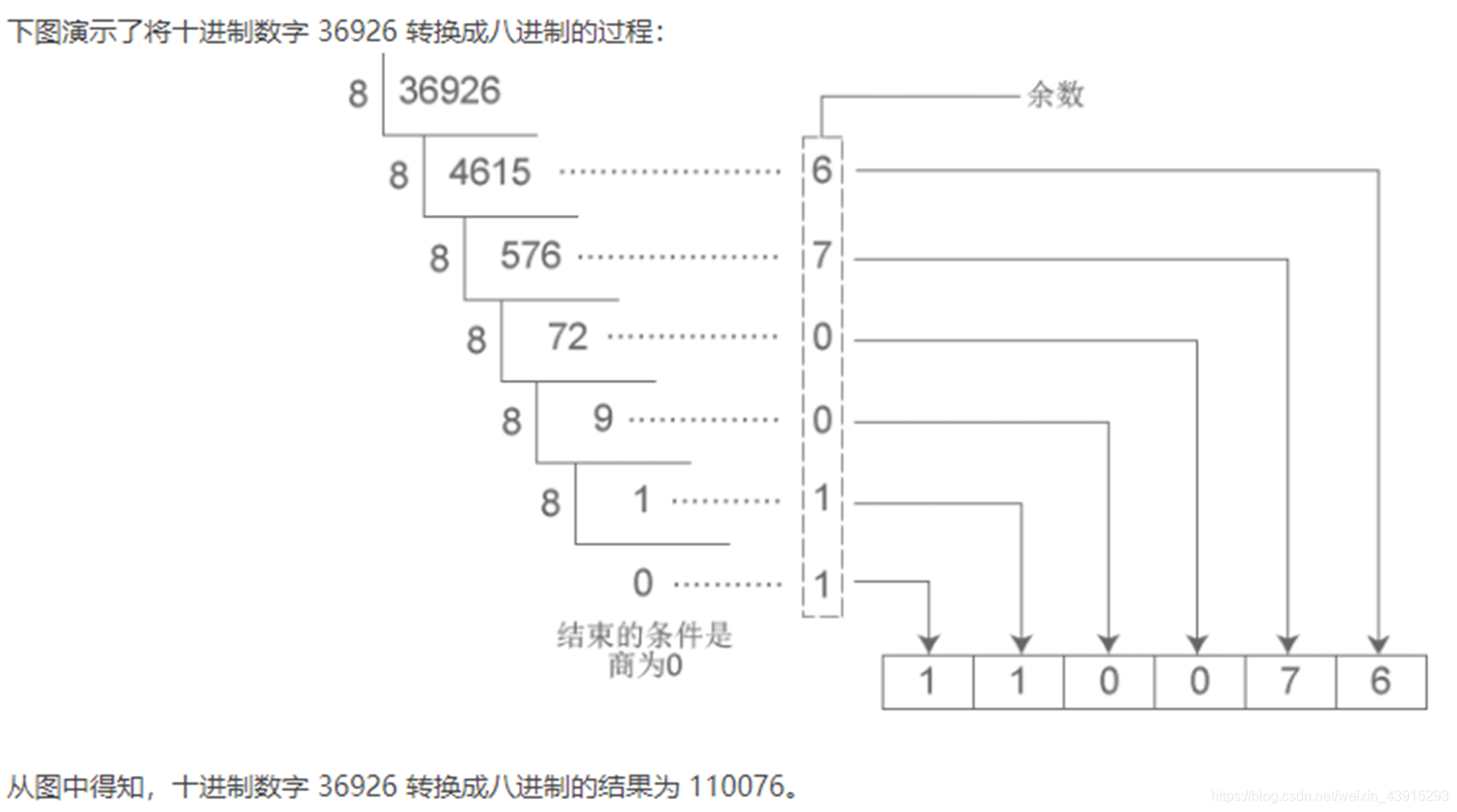
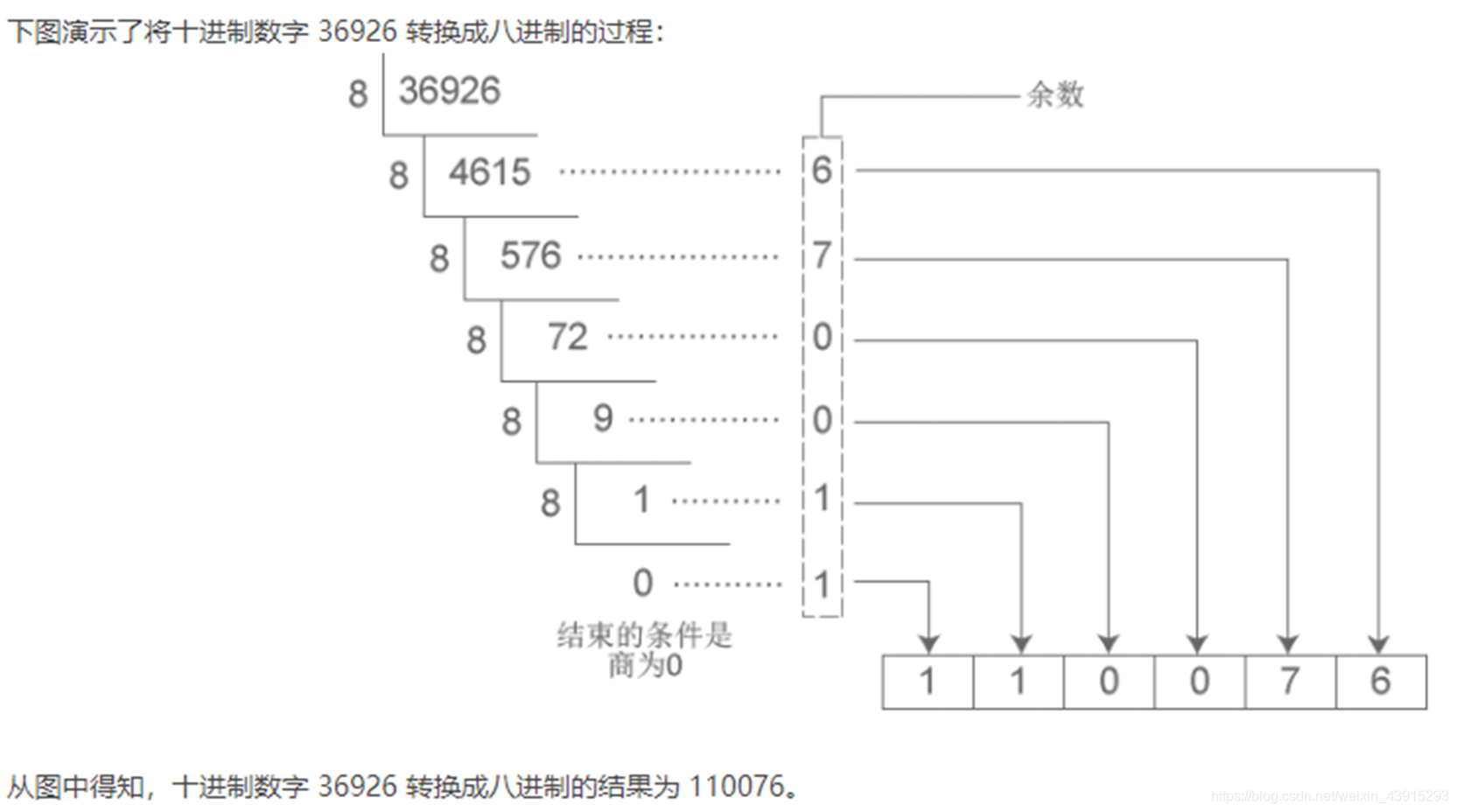
示例:十进制 123 → 二进制
123 ÷ 2 = 61 余 1
61 ÷ 2 = 30 余 1
30 ÷ 2 = 15 余 0
15 ÷ 2 = 7 余 1
7 ÷ 2 = 3 余 1
3 ÷ 2 = 1 余 1
1 ÷ 2 = 0 余 1
从下往上读取余数:1111011,补全为8位:0B01111011
示例:十进制 100 → 八进制
100 ÷ 8 = 12 余 4
12 ÷ 8 = 1 余 4
1 ÷ 8 = 0 余 1
结果:0144
示例:十进制 123 → 十六进制
123 ÷ 16 = 7 余 11(B)
7 ÷ 16 = 0 余 7
结果:0x7b
3. 二进制与其他进制的快速转换
a. 二进制 → 八进制
- 原理:3位二进制 = 1位八进制(因为 23=82^3 = 823=8)
- 方法:从右往左每3位一组,不足补0,每组转为八进制数
示例:
二进制:0B10100101011110011
分组:101 001 010 111 100 11(补0 → 011)
转换:5 1 2 7 4 3
结果:0512743
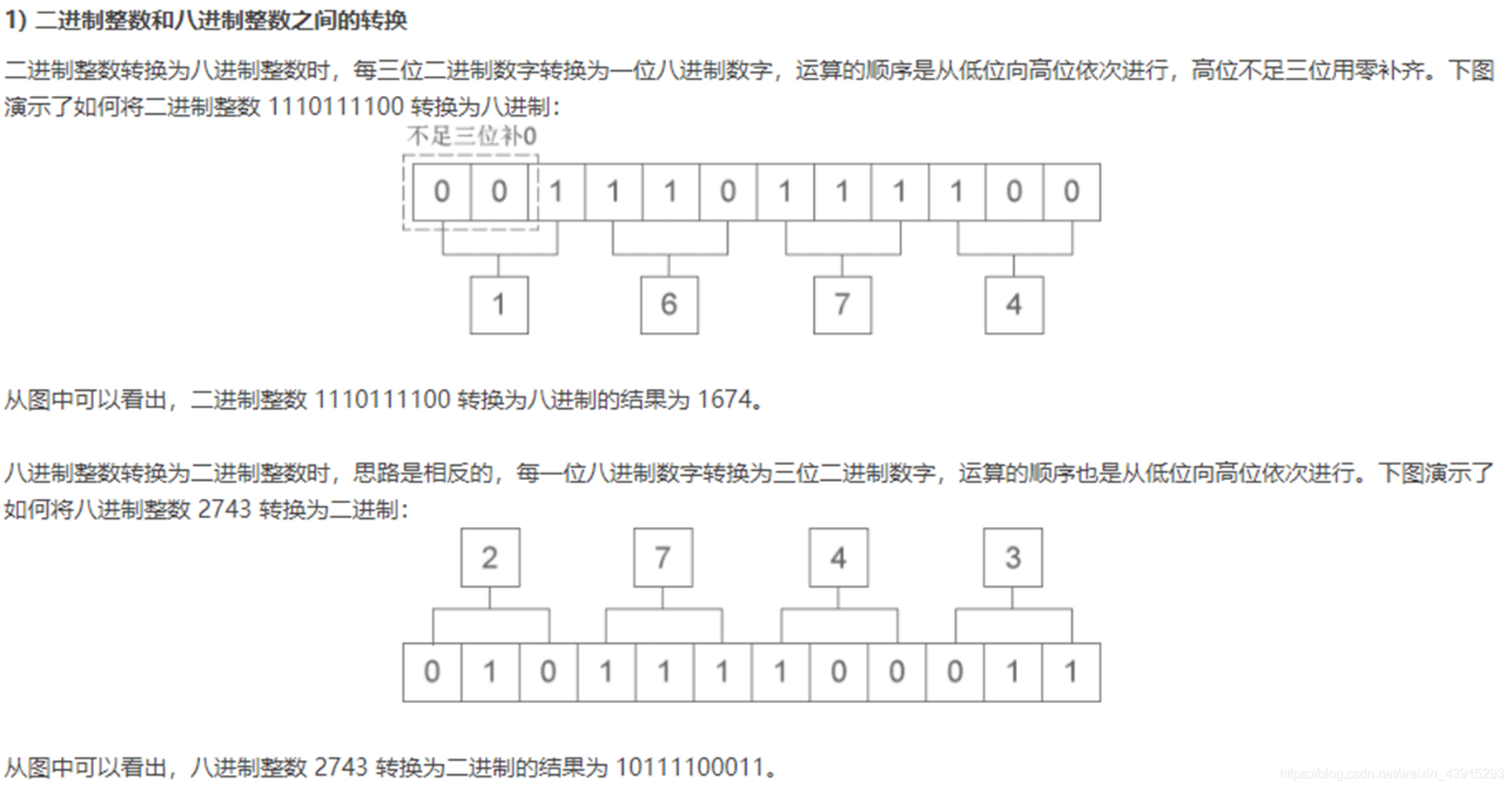
b. 二进制 → 十六进制
- 原理:4位二进制 = 1位十六进制(因为 24=162^4 = 1624=16)
- 方法:从右往左每4位一组,不足补0,每组转为十六进制数
示例:
二进制:0B00010101001010101010
分组:0001 0101 0010 1010 1010
转换:1 5 2 A A
结果:0x152AA

四、负数的表示(以二进制为例)
在计算机中,负数使用补码表示。
步骤:
- 求原码:正数的二进制表示
- 求反码:按位取反(符号位不变)
- 求补码:反码 + 1
示例:-100 的二进制表示
- 原码:100 =
01100100(假设8位) - 反码:
10011011 - 补码:
10011100
所以,-100 的二进制补码表示为:0B10011100
五、总结
| 进制 | 基数 | 符号范围 | 表示前缀 | 特点 |
|---|---|---|---|---|
| 十进制 | 10 | 0~9 | 无 | 日常使用 |
| 二进制 | 2 | 0,1 | 0B | 计算机基础 |
| 八进制 | 8 | 0~7 | 0 | 简化二进制 |
| 十六进制 | 16 | 0~9, A~F | 0x | 内存地址、颜色代码 |
进制加减法
以下是对进制加减法相关内容的优化叙述,逻辑更清晰、结构更严谨:
进制基础与加减法运算规则
在计算机科学和编程中,理解不同进制及其运算规则是非常重要的基础知识。常见的进制包括二进制、八进制、十进制和十六进制。它们的核心区别在于所使用的数字范围和进位规则。
一、二进制(Binary)
- 表示方式:使用两个数字
0和1来表示数值。 - 应用场景:计算机内部所有数据都以二进制形式存储和处理。
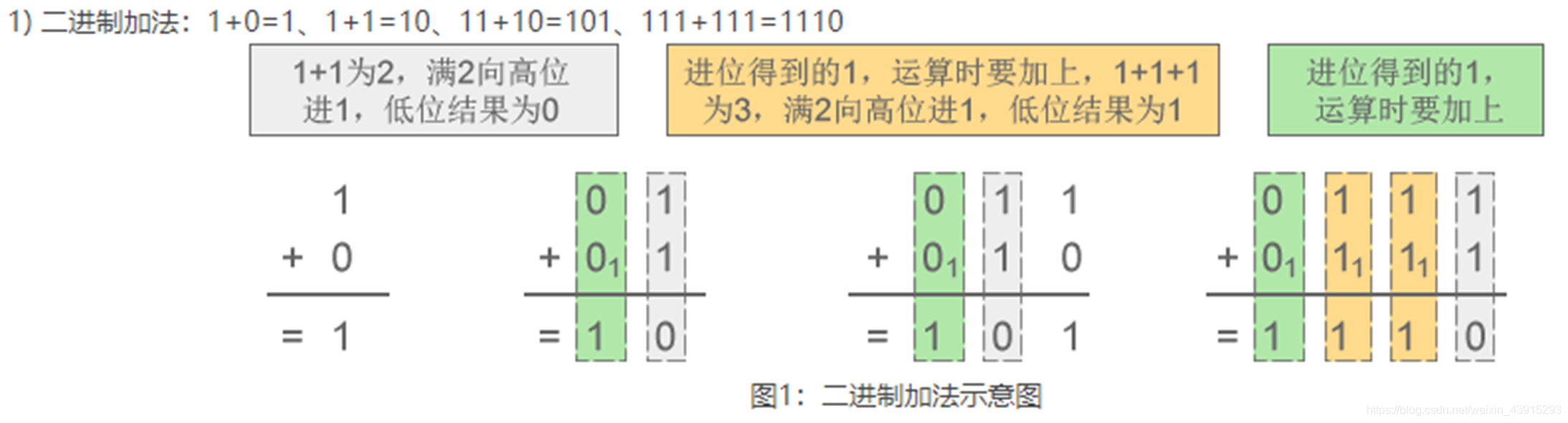
- 加法规则:逢二进一。
例如:1 + 1 = 10 - 减法规则:借一当二。
例如:10 - 1 = 1
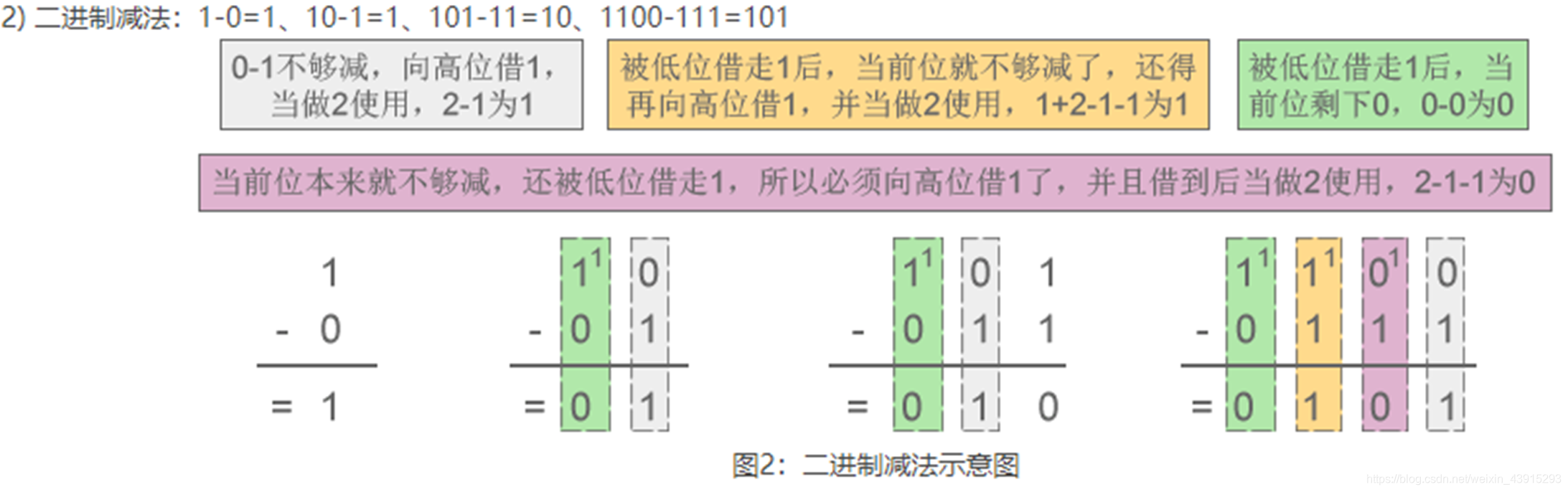
二、八进制(Octal)
- 表示方式:使用八个数字
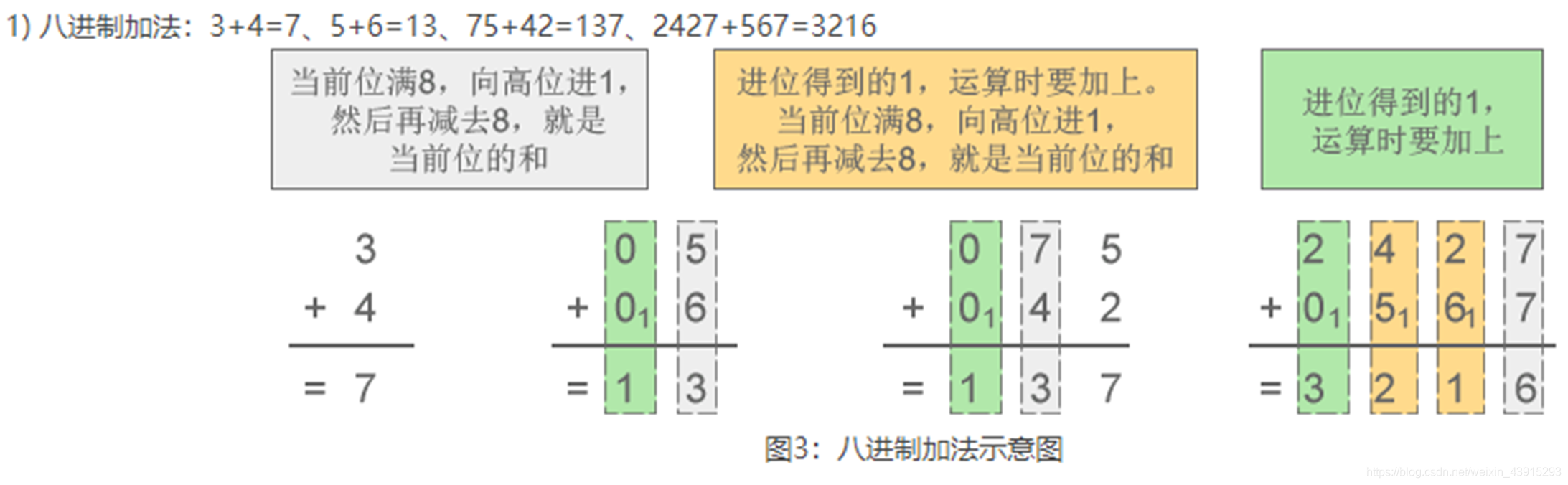
0到7来表示数值。 - 加法规则:逢八进一。
例如:7 + 1 = 10 - 减法规则:借一当八。
例如:10 - 1 = 7
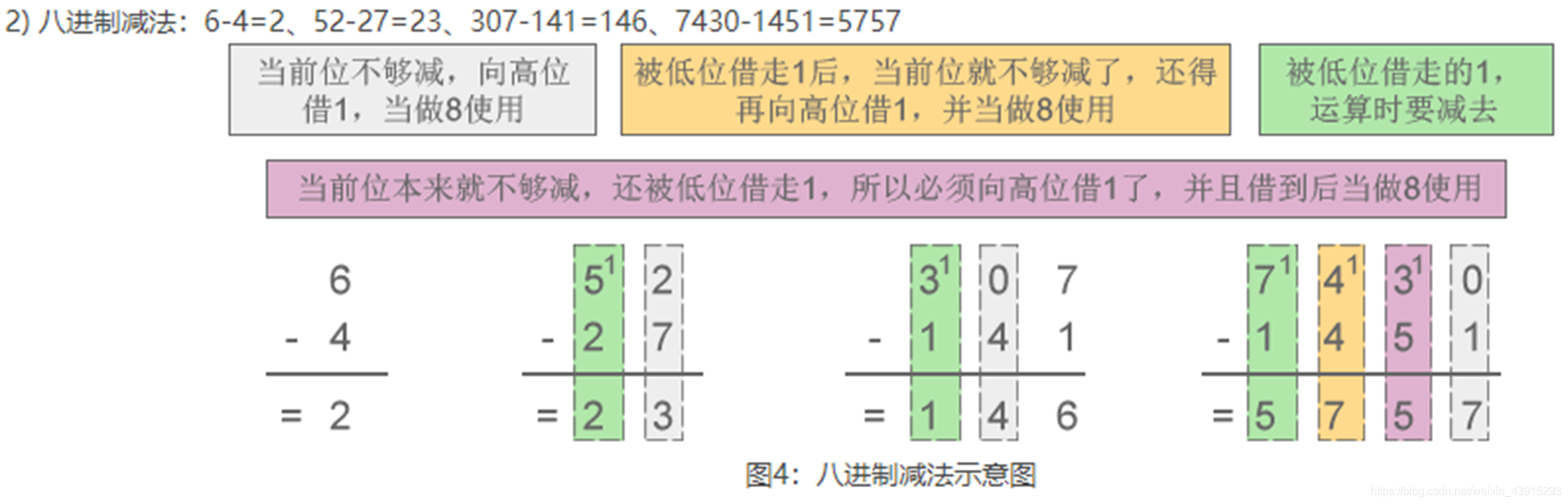
三、十进制(Decimal)
- 表示方式:使用十个数字
0到9来表示数值。 - 加法规则:逢十进一。
- 减法规则:借一当十。
四、十六进制(Hexadecimal)
- 表示方式:使用数字
0到9和字母A到F来表示数值。
其中:- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
- 字母说明:不区分大小写,
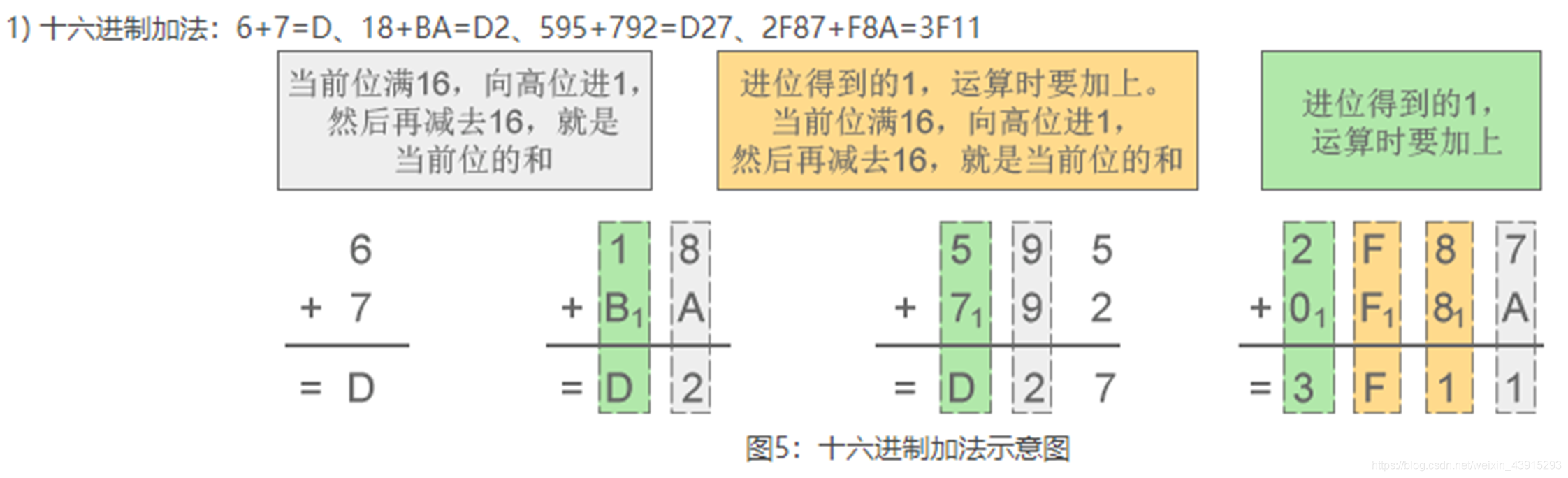
ABCDEF也可以写作abcdef。 - 加法规则:逢十六进一。
例如:F + 1 = 10 - 减法规则:借一当十六。
例如:10 - 1 = F
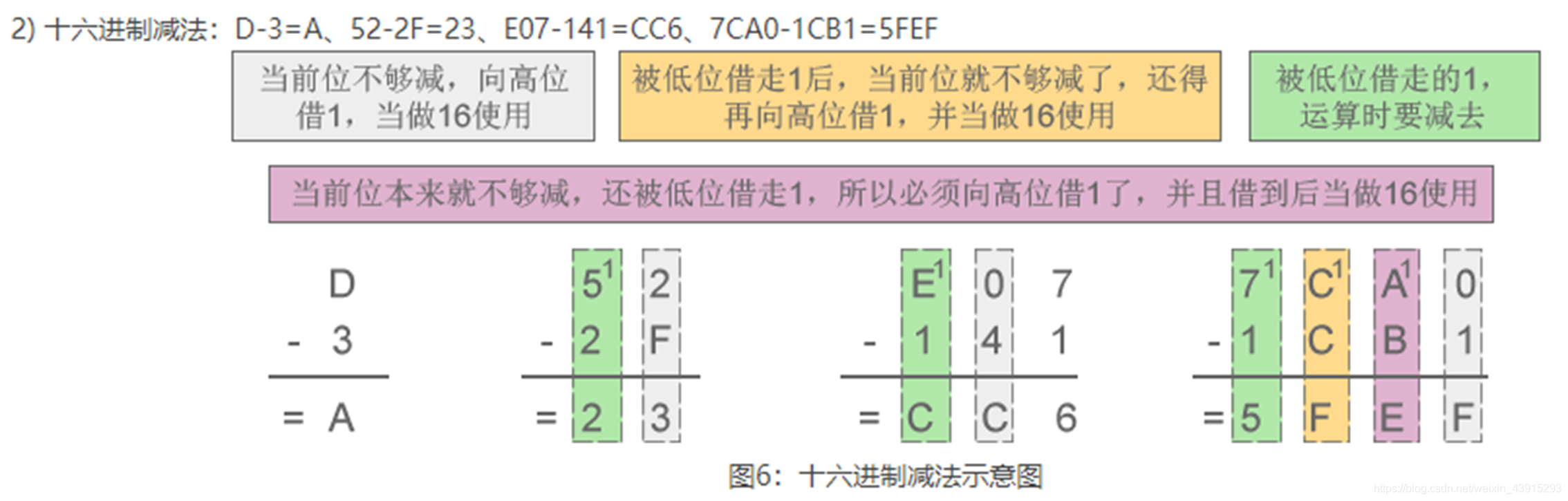
总结
不同进制的加减法遵循相同的逻辑:
- 加法:当前位满“基数”就向前一位进一;
- 减法:当前位不够减时,向高位借一,相当于借了“基数”。
掌握这些规则,有助于理解数据在计算机中的表示和处理方式,是学习编程和计算机系统的重要基础。
进制对照表

