GJOI 5.24 题解

1.AT_abc320_d Relative Position

题意

思路

考场时 GJ 都不说保证关系是否矛盾，虚空讨论了半小时，最终还是查原题才知道是一道很水的题 ，反正就是写出来了。

$x$ 和 $y$ 的关系既然知道，但是不知道这些点是否有前继，不妨直接对 $x,y$ 建边，双向边权分别是二元组 $(a,b)$ 和 $(-a,-b)$。从已知的 $1(0,0)$ 开始 dfs 即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,inf=3e14;
ll n,m;
ll idx,head[N];
struct edge
{ll to,next,dx,dy;
}e[N<<1];
void addedge(ll u,ll v,ll dx,ll dy)
{idx++;e[idx].to=v;e[idx].next=head[u];e[idx].dx=dx;e[idx].dy=dy;head[u]=idx;
}
bool vis[N];
ll px[N],py[N];
void dfs(ll u)
{vis[u]=1;for(int i=head[u];i;i=e[i].next){ll v=e[i].to,dx=e[i].dx,dy=e[i].dy;if(vis[v])continue;px[v]=px[u]+dx,py[v]=py[u]+dy;dfs(v);}
}
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=m;i++){ll x,y,a,b;scanf("%lld%lld%lld%lld",&x,&y,&a,&b);addedge(x,y,a,b);addedge(y,x,-a,-b);}for(int i=2;i<=n;i++)px[i]=py[i]=inf;dfs(1);for(int i=1;i<=n;i++){if(px[i]==inf)puts("undecidable");else printf("%lld %lld\n",px[i],py[i]);}return 0;
}

2.AT_abc320_e Somen Nagashi

题意

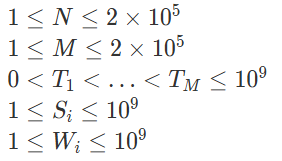
思路

把事件开始时间和结束时间离散化之后，直接按照时间轴模拟事件即可。

编号总是有序的，所以我们可以拿一棵平衡树（笑），维护删数和插入操作。删数的时候我们获取对头之后，根据对应的结束时间 $t$，我们开一个 vector 来统计时间 $t$ 要加入哪些点。

注意在 $X$ 时刻返回队列的也算在队列里，所以要先加点再删点。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=4e5+9,M=6e5+9,inf=3e10;
ll n,m;
ll rt,cnt;
struct Node
{ll ls,rs;ll val,pri;//键值 随机优先级 ll siz;//子树大小 
}T[N];
void newNode(ll x)
{cnt++;T[cnt].siz=1;T[cnt].ls=T[cnt].rs=0;T[cnt].val=x;T[cnt].pri=rand();
}
void pushup(ll u)
{T[u].siz=T[T[u].ls].siz+T[T[u].rs].siz+1;
}
void split(ll u,ll k,ll &L,ll &R)//分裂操作 
{if(u==0){L=R=0;return;}if(T[u].val<=k){L=u;split(T[u].rs,k,T[u].rs,R);}else {R=u;split(T[u].ls,k,L,T[u].ls);}pushup(u);
}
ll merge(ll L,ll R)//合并两棵根为L和R的树，返回树根 
{if(!L||!R)return L|R;if(T[L].pri>T[R].pri){T[L].rs=merge(T[L].rs,R);pushup(L);return L;}else {T[R].ls=merge(L,T[R].ls);pushup(R);return R;}
}
void insert(ll x)//插入一个数x 
{ll L,R;split(rt,x,L,R);newNode(x);rt=merge(merge(L,cnt),R);
}
void del(ll x)//删除一个数x
{ll L,R,u;split(rt,x,L,R);//<=x的树和>x的树 split(L,x-1,L,u);//<x的树和=x的树 u=merge(T[u].ls,T[u].rs);//合并<x和>x的树，就删除了x rt=merge(merge(L,u),R);
}
ll kth(ll u,ll k)//排名为k的节点编号 
{if(k==T[T[u].ls].siz+1)return u;if(k<=T[T[u].ls].siz)return kth(T[u].ls,k);//目标在左return kth(T[u].rs,k-T[T[u].ls].siz-1);//目标在右
}
ll tot,nn,aa[M];
ll ans[N];
struct que
{ll st,en,w;
}a[N];
struct term
{ll op,w;ll en;
};
vector<term>p[M];
vector<ll>back[M];
int main()
{srand(time(0));scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++)insert(i);for(int i=1;i<=m;i++){ll t,w,s;scanf("%lld%lld%lld",&t,&w,&s);a[i]=(que){t,t+s,w};aa[++tot]=t;aa[++tot]=t+s;}sort(aa+1,aa+tot+1);nn=unique(aa+1,aa+tot+1)-aa-1;for(int i=1;i<=m;i++){a[i].st=lower_bound(aa+1,aa+nn+1,a[i].st)-aa;a[i].en=lower_bound(aa+1,aa+nn+1,a[i].en)-aa;p[a[i].st].push_back((term){1,a[i].w,a[i].en});p[a[i].en].push_back((term){-1,inf,inf});}ll len=n;for(int i=1;i<=nn;i++){for(auto t:back[i]){len++;insert(t);}for(auto x:p[i]){if(x.op==1){if(len){len--;ll t=T[kth(rt,1)].val;ans[t]+=x.w;back[x.en].push_back(t);del(t);}}}}for(int i=1;i<=n;i++)printf("%lld\n",ans[i]);return 0;
}

这个方法还是太笨拙了，其实不如用两个优先队列，一个维护事件、一个维护返回时间和节点。

3.AT_abc320_f Fuel Round Trip

题意

思路

考虑 dp，但是这题很奇怪，既要过去又回来。

一开始我想着变成一条 $2n$ 的路，但是有只能使用每个加油站一次的限制，这是有后效性的，没办法 dp。

如果只用从 $0$ 到 $x_n$ 的话，我们当然设 $f_{i,j}$ 表示走到第 $i$ 个加油站，邮箱剩下 $j$ 的油的最小花费。那么若 $d=x_i-x_{i-1}$：

• 第 $i$ 个加油站不加油： f i , j − d = min ⁡ { f i − 1 , j } f_{i,j-d}=\min\{f_{i-1,j}\} fi,j−d​=min{fi−1,j​}；
• 第 $i$ 个加油站加油： f i , j − d + F i = min ⁡ { f i − 1 , j + P i } f_{i,j-d+F_i}=\min\{f_{i-1,j}+P_i\} fi,j−d+Fi​​=min{fi−1,j​+Pi​}。

其实我们可以对这个做法拓展，反正这里的 $n,H$ 够小，我们直接设 $f_{i,j,k}$ 表示顺向走到第 $i$ 个加油站，顺向剩下 $j$ 的油、走回来时剩下 $k$ 的油的最小花费。初始化 $F_{0,H,0}=0$（开始时带 $H$ 的油），其余全部极大值。

这时候我们要分三种情况：

• 第 $i$ 个加油站不加油： f i , j − d , k + d = min ⁡ { f i − 1 , j , k } f_{i,j-d,k+d}=\min\{f_{i-1,j,k}\} fi,j−d,k+d​=min{fi−1,j,k​}；
• 第 $i$ 个加油站顺向时加油： f i , j − d + F i , k + d = min ⁡ { f i − 1 , j , k + P i } f_{i,j-d+F_i,k+d}=\min\{f_{i-1,j,k}+P_i\} fi,j−d+Fi​,k+d​=min{fi−1,j,k​+Pi​}；
• 第 $i$ 个加油站回来时加油： f i , j − d , k + d − F i = min ⁡ { f i − 1 , j , k + P i } f_{i,j-d,k+d-F_i}=\min\{f_{i-1,j,k}+P_i\} fi,j−d,k+d−Fi​​=min{fi−1,j,k​+Pi​}。

我们画个图帮助理解：

注意加油的上限和对 $0$ 取 $\max$。

最后的答案就是 max ⁡ i = 0 H max ⁡ j = 0 i { f n , i , j } \displaystyle\max_{i=0}^H\max_{j=0}^i\{f_{n,i,j}\} i=0maxH​j=0maxi​{fn,i,j​}，因为在中点 $x_n$ 没有加油站，回去的油不能凭空比顺向的油多。

注意到 $n,H$ 同阶，时间复杂度 $\Theta (n^3)$。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=302,inf=0x3f3f3f3f;
ll n,H,x[N],P[N],F[N];
ll f[N][N][N];
ll chg(ll x)
{return max(min(x,H),0ll);
}
int main()
{scanf("%lld%lld",&n,&H);for(int i=1;i<=n;i++)scanf("%lld",&x[i]);for(int i=1;i<n;i++)scanf("%lld%lld",&P[i],&F[i]);memset(f,inf,sizeof(f));f[0][H][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=H;j++){for(int k=0;k<=H;k++){ll d=x[i]-x[i-1];if(j-d<0||k+d>H)continue;f[i][j-d][k+d]=min(f[i][j-d][k+d],f[i-1][j][k]);f[i][chg(j-d+F[i])][k+d]=min(f[i][chg(j-d+F[i])][k+d],f[i-1][j][k]+P[i]);f[i][j-d][chg(k+d-F[i])]=min(f[i][j-d][chg(k+d-F[i])],f[i-1][j][k]+P[i]);}}}ll ans=inf;for(int i=0;i<=H;i++){for(int j=0;j<=i;j++){//	cout<<f[n][i][j]<<" ";ans=min(ans,f[n][i][j]);//终点不能凭空加油 }//	cout<<endl;}if(ans>=inf)puts("-1");else printf("%lld",ans);return 0;
}

4.AT_abc319_g Counting Shortest Paths

本题解参考了这篇。

题意

思路

假若我们知道这个图确切地长什么样，我们就 bfs 确定最短路径和方案数，时间复杂度 $\Theta (n^2)$。

但是现在是一幅有 $2\times 10^5$ 级别点数的稠密图！因此我们要在删除的边集上操作。我们要考虑每个 $i$ 的 $1\to i$ 的最短路径长度进行分层。

我们设现图边集 $E_0$，删边边集 $E^{\prime }$

设 $f_i$ 表示 $1\to i$ 的最短路径条数，$s_{di{s}_i}$ 表示和 $i$ “同一层”的节点 $v$ 的 $\sum f_v$。

我们转移 $f_u$，从上一层的 $v$ 转移过来，那么：
$$f_u=\sum _{(u,v)\in E_0}{f}_v(di{s}_u=di{s}_v+1)$$
现图其实我们不知道，但是上一层的所有 $v$ 用 $s$ 维护了，而删边边集是已知的，因此“整体减空白”：$$=\sum f_v-\sum _{(u,v)\in E^{\prime }}{f}_v(di{s}_u=di{s}_v+1)$$
$$=s_{di{s}_u}-\sum _{(u,v)\in E^{\prime }}{f}_v(di{s}_u=di{s}_v+1)$$

while(!q.empty())
{ll u=q.front();q.pop();if(u!=1)f[u]=s[dis[u]-1];for(auto v:G[u])//不连接的点 {vis[v]=1;if(dis[v]==dis[u]-1)f[u]=(f[u]-f[v]+mod)%mod;}if(u==n)break;s[dis[u]]=(s[dis[u]]+f[u])%mod;
}

扩展新的点，我们就记录所有没有被搜索到的点。那么搜索到一个新点的时候，就可以只对那些没有被搜到且在新图中和当前点相连的点就行了。因为只有那些被删除的边会重复被标记，而其它点只会被标记一次，所以这一部分是 $\Theta (n+m)$ 的。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9,inf=0x3f3f3f3f,mod=998244353;
ll n,m;
vector<ll>G[N],rest;
ll dis[N],f[N],s[N];//每一层的f(i)和 
bool vis[N];//遍历删除边上的点 
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=m;i++){ll u,v;scanf("%lld%lld",&u,&v);G[u].push_back(v);G[v].push_back(u);}queue<ll>q;for(int i=2;i<=n;i++){rest.push_back(i);dis[i]=inf;}dis[1]=0;f[1]=1;q.push(1);while(!q.empty()){ll u=q.front();q.pop();if(u!=1)f[u]=s[dis[u]-1];for(auto v:G[u])//不连接的点 {vis[v]=1;if(dis[v]==dis[u]-1)f[u]=(f[u]-f[v]+mod)%mod;}if(u==n)break;s[dis[u]]=(s[dis[u]]+f[u])%mod;vector<ll>trest;for(auto v:rest){if(vis[v])trest.push_back(v);else {dis[v]=dis[u]+1;q.push(v);}}rest=trest;for(auto v:G[u])vis[v]=0;}if(dis[n]==inf)puts("-1");else printf("%lld",f[n]);return 0;
}

5.AT_abc320_g Slot Strategy 2 (Hard)