再论自然数全加和-2
对于质数来说，不仅有正质数，还有负的质数，如果不考虑2，则，
的形式，就可以导出负的质数。这一点我们暂时先记住，后面会用到。
首先考虑如下形式，
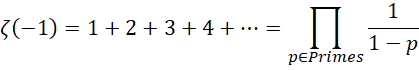
带入前几个质数，
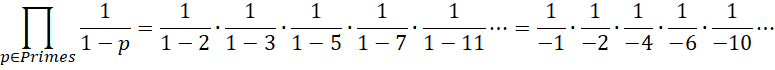
这个结果的正负不定，但每一项都是一个分数形式，从其特征可以看出，比如 
这里的-1，不是比0小，而是比无限小1，也就是说它其实是虚数单位的平方。它的倒数实际上就是周期的倒数而这个数就是无穷小。后面的 
可以认为是比周期小1的数量的倒数，也是某种无穷小。后面其它的负分数都是如此。由此可见，这个结果本质上是一种无限阶的高阶无穷小。每一个阶都是一个无穷大的倒数。换句话说，
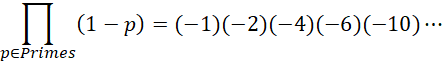
方程的右侧就是一系列无穷大的乘积。我们知道在这个乘积中，每一个项都是一个维数的度量，比如第0维，第1维，第2维等等。因为每一个维数都是无穷大的，相邻维数相乘就构成高维的复合。对于追求有限结果的我们来说，我们并不需要无限维，我们只需要有限维数，这样才有可能获得有限的结果。
具体来说，我们先写出这些维数的长度（虽然是负数但先按照正数来写，最后决定符号）的乘积，再判断结果的符号，
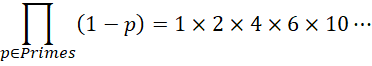
如果取0维，则得到1也就是单位1，后面剩下偶数个负数也就是偶数个-1的倍数，这些-1全部相乘结果为1；如果取1维，也就是 
，包含第0和第1维，则后面剩下奇数个负数，这些-1全部相乘结果为-1，那么这个数就等于-2；如果取2维，也就是 
，则后面剩下偶数个-1，相乘结果为1，这个数等于8……，以此类推，结果奇偶相间。
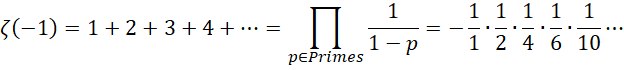
各个维数的数值为，
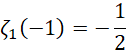
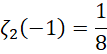
所以实际上就是各次的高阶无穷小。0次的就是周期本身，1次的就是整体的一半，假定整体为0，二次的就是整体的八分之一，以此类推。
从这个结果可以看出，泽塔函数的数值，其实就是和整体的相对关系。和虚数单位定义一样，0代表下一个周期的开始，-1代表周期本身，1代表单位或者周期的平方模周期之后的余量。
以上是从正质数的角度理解，得到的结果。但这个结果显然不是我们想要的。因为，所谓维数，来自于对空间的认识，显然是尽可能大的数值意味着更高的维数，而从后往前倒着数则保证了数值尽可能的大。所以说一个三维空间显然是数值最大的三个度量构成的空间，而其它更小的度量则被认为是空间中的细节。所以这里考虑维数的时候，也是从倒着数的质数，也就是负质数开始的。
由此，
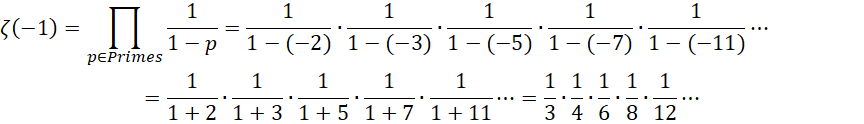
显然结果仍然是无限阶的无穷小，我们也为其添加单位1，
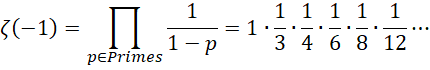
它的0维截断，因为1是后来添加的，所以后面有奇数个负数，奇数个-1相乘为-1，所以0维的大小为-1；它的1维截断，后面有偶数个-1相乘，偶数个-1相乘为1，结果为 
。它的2维截断，后面有奇数个-1相乘，奇数个-1相乘为-1，所以，
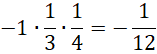
这才是我们期望的结果。计算二维截断得到这个结果，是因为，
本身就是一种“梯形”的二维结构，所以选取前三项构成它的数值。也就是说，在二维前提下，它的数量为整体作为单位1的十二分之十一(11/12)。
虽然，
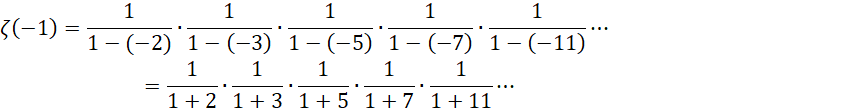
每一项都是正数，但是实际上都是1减去一个极大的数，此时的0体现为下一个周期的开始，结果是负数。具体来说，如果这个周期为N，则上式可以写成，
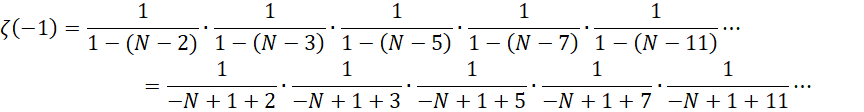
因为N非常大，所以显然可见的每一项都是负数（只可能有有限个正数或者0）。
对于这种结构，事实上我们还可以用虚数单位的形式来描述，
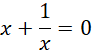
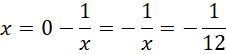
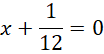
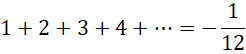
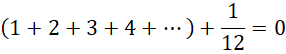
可见，12就是这个系统在倒着计数前提下的二维虚数单位（类比于 
，它的周期为144+1=145），它的倒数(1/12)为“半阶”无穷小。