简说IMM

1. 基本概念和表述

齐次马尔科夫链

其次马尔可夫链的转移过程可表述为：
P i j { m j ( k + 1 ) ∣ m i ( k ) } = p i j ∀ i , j ∈ M f P_{ij}\{m_j(k+1)|m_i(k)\}=p_{ij} \qquad \forall i,j \in M_f Pij​{mj​(k+1)∣mi​(k)}=pij​∀i,j∈Mf​
易理解，$p_{ij}$表达了由$k$时刻的模型$i$转移到$k+1$时刻的模型$j$的概率

文中符号说明

• $M_f$ 表示模型空间，IMM表达多个模型都属于这个模型空间
• 下标$i,j$：
  • 当有一个下标时，一般表示某个模型的变量，如${\mu }_i$表示模型i的概率
  • 当有两个下标时，用来表示两个模型间的转移，如KaTeX parse error: Undefined control sequence: \p at position 1: \̲p̲_{ij}表示模型i转移到模型j的概率
  • 当有两个下标中间有竖线"|"时，表示归一化的信息
• $\hat{\cdot }$ Hat 表示这个变量是某个条件下的最优估计
• 括号()：表示时间，如$x(k)$表示时间k的状态x；
• 括号中有竖线：表示观测时间和状态时间，如x(k|k-1)表示在k-1时刻的观测信息得到k时刻的状态，如x(k|k)表示基于k时刻的观测估计的k时刻的状态

2. IMM过程

先有个基本概念，整个过程可描述为：

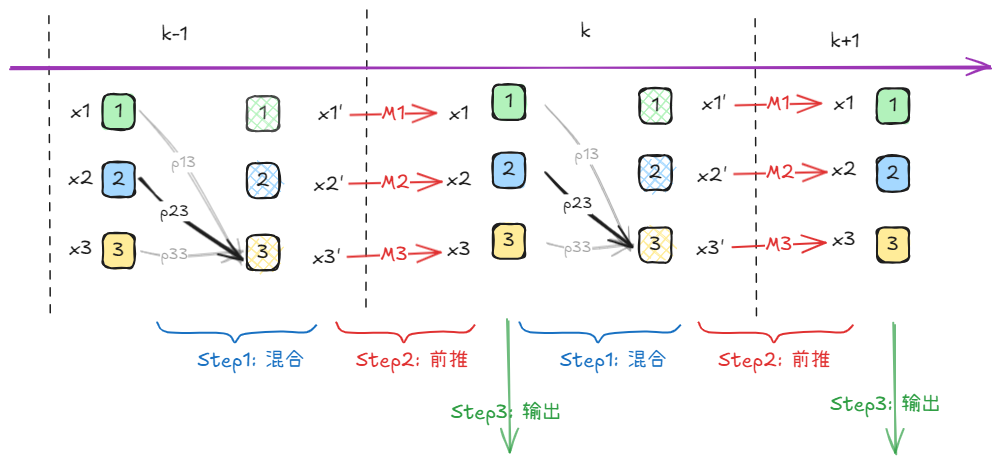
Step1: Interact

交互，顾名思义，就是多个模型之间的交互。

$\forall i,j\in M_f$
$$\begin{array}{c}{\mu }_{i|j}(k-1|k-1)=\frac{1}{{\bar{c}}_j}{p}_{ij}{\mu }_i(k-1)\end{array}$$

解释：

• ${\mu }_i(k-1)$是k-1时刻，模型$i$的概率
• ${\mu }_{i|j}(k-1|k-1)$ 表示的就是k-1时刻，模型i转移的j的混合概率；
• 这个公式表达的还是在k-1时刻的进行的估计，是基于k-1时刻的观测和状态，对下一个状态概率的预估
• 为了描述方便，本章节中的变量都略去时刻的表述$(k-1|k-1)$

式(1)这个过程表达了模型i到模型j转移的混合概率，其实就是在转移概率$p_{ij}$的基础上混合了当前状态i模型的概率

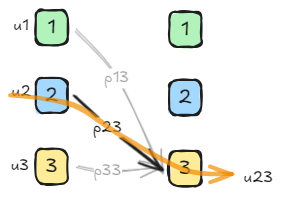
如图，$u_{23}$表达的是从模型2转移到模型3的概率，混合上当前的模型2的概率
可以表达为

$$\begin{gathered} \left[\begin{array}{ccc}{\mu }_{11}& {\mu }_{12}& {\mu }_{13}\end{array}\right]=\left[\begin{array}{ccc}{p}_{11}& p_{12}& p_{13}\end{array}\right]{\mu }_1 \\ \left[\begin{array}{ccc}{\mu }_{21}& {\mu }_{22}& {\mu }_{23}\end{array}\right]=\left[\begin{array}{ccc}{p}_{21}& p_{22}& p_{23}\end{array}\right]{\mu }_2 \\ \left[\begin{array}{ccc}{\mu }_{31}& {\mu }_{32}& {\mu }_{33}\end{array}\right]=\left[\begin{array}{ccc}{p}_{31}& p_{32}& p_{33}\end{array}\right]{\mu }_3 \end{gathered}$$
然后还要归一化一次，表示了转移到模型$i\in [1,3]$的一致性概率，可以理解为，$u_{i1}$表示从上一时刻多个模型转移到模型1的概率，归一化是所有转移到模型1的概率。有点绕，看公式
$$\begin{array}{c}{\mu }_{2|3}=\frac{{\mu }_{23}}{{\mu }_{13}+{\mu }_{23}+{\mu }_{33}}\end{array}$$

注：先不要纠结为什么这里要归一化概率，后面会解释

无论什么模型，目的都是为了获得对当前状态的估计。当我们使用多个模型对状态进行估计时，会得到不同模型对状态估计的结果，然后我们将这些结果加权，就得到了多模型混合估计结果。

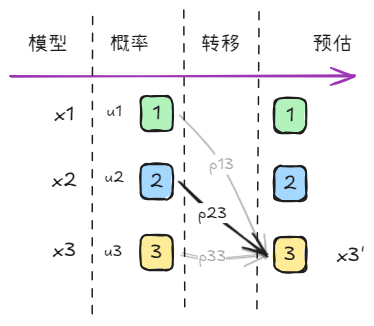
对于上图中的模型转移过程，如果我们要求模型3的预估状态$x_3^{\prime }$，很容易想到，通过加权来获得
$$x_3^{\prime }=\frac{x_1\cdot p_{13}{\mu }_1+x_2\cdot p_{23}{\mu }_2+x_3\cdot p_{33}{\mu }_3}{p_{13}{\mu }_1+p_{23}{\mu }_2+p_{33}{\mu }_3}$$
显然，式（2）就是这个权重。
即
$$x_3^{\prime }=x_1\cdot {\mu }_{1|1}+x_2\cdot {\mu }_{2|1}+x_3\cdot {\mu }_{1|3}$$

总结下，Step1得到了对状态的估计模型$x^{\prime }$，论文中记${\hat{x}}_{0j}$，有了状态我们还需要相关协方差$P$，同样，协方差的更新于状态量类似，

$${\hat{P}}_3=P_1^{\prime }\cdot {\mu }_{1|1}+P_2^{\prime }\cdot {\mu }_{2|1}+P_3^{\prime }\cdot {\mu }_{1|3}$$
其中
$$P_1^{\prime }=P_1+({\hat{x}}_3^{\prime }-x_1)\times ({\hat{x}}_3^{\prime }-x_1{)}^T$$

公式表示即为：
$$\begin{array}{c}{\hat{P}}_j=\sum _i{P}_i^{\prime }\cdot {\mu }_{i|j}=\sum _i[P_i+({\hat{x}}_{j0}-x_i)\times ({\hat{x}}_{j0}-x_i{)}^T]\cdot {\mu }_{i|j}\end{array}$$

再来理解一下这些变量的含义，$u_{13},u_{23},u_{33}$是所有模型转移到模型3的概率，记
$${\bar{c}}_j=u_{1j}+u_{2j}+u_{3j}=\sum _i{\mu }_{ij}=\sum _i{p}_{ij}{u}_i$$

---

Step 2: Filtering

在Step1中，都是在k-1时刻发生的，因为模型本身并没有进行时域上的前推，现在我们需要对每个模型都通过模型参数预测（前推）一步，所以Step2要进行时序的推演，则状态和协方差的转移可以表述为：$\forall j\in M_f$,
$${\hat{x}}_j(k|k-1)=F_j(k-l){\hat{x}}_j(k-1|k-1)+{\Gamma }_j(k-i){\bar{v}}_j(k-1)$$
其中$\Gamma$是过程噪声增益矩阵。
由于公式中的变量为了描述时序信息（k/k-1），看起来有点混乱，为了便于理解，可以描述为：
$${\hat{x}}_j^{(k)}=F_j{\hat{x}}_j^{(k-1)}+{\Gamma }_j{\bar{v}}_j$$
同理，协方差的推演表述为：
$$P_j^{(k)}=F_j{P}_j^{(k-1)}{F}_j^T+{\Gamma }_j{Q}_j{\Gamma }_j^T$$
其中$Q_J$为过程噪声方差。

以上是都是在k-1时刻观测下进行的计算和推演，当来到了k时刻，有了新的观测，就需要进行Correct操作了，这时候的观测时序变成了k，可以，表述为：
$$\begin{gathered} {\hat{x}}_j(k|k)={\hat{x}}_j(k|k-1)+W_j(k)r_j(k) \\ {P}_j(k|k)=P_j(k|k-1)-W_j(k)S_j(k)W_j(k{)}^T \end{gathered}$$
其中：

• $r_j(k)=z_j(k)-{\hat{z}}_j(k|k-1)$表达了观测残差，计算方式为：
  $${\hat{z}}_j(k|k-1)=H_j(k){\hat{x}}_j(k|k-1)$$
• $R_j(k)$为测量方差
• $S_j(k)$为残差方差，计算方式为
  $$S_j(k)=H_j(k)P_j(k|k-1)H_j(k{)}^T+R_j(k)$$
• $W_j(k)$表示滤波器增益矩阵，计算方式为
  $$W_j(k)=P_j(k|k-1)H_j(k)S_j(k{)}^{-1}$$

根据观测的残差，可以根据残差计算出模型j的likehood，
$${\Lambda }_j(k)=N(r_j(k),0,S_j(k))$$

根据模型j的likehood，来更新模型j的概率
$${\mu }_j^{\prime }(k)={\Lambda }_j(k){\bar{c}}_j$$
归一化之后为
$$\begin{array}{c}{\mu }_j(k)=\frac{{\mu }_j^{\prime }(k)}{{\sum }_i{\mu }_i^{\prime }(k)}\end{array}$$

总结下，Step2主要进行了：

1. 基于模型的推演，得到推演后模型的状态估计及协方差
2. 基于推演模型状态和观测的残差，得到每个模型的likehood
3. 基于likehood，推演出每个模型新的概率

---

Step3: Combination

Combination这一步非常简单，就是将多个模型的输出加权，得到对外的最终输出估计，即
$$\hat{x}(k|k)=\sum _j{\hat{x}}_j(k|k){\mu }_j(k)$$
同理，输出的协方差为
$$P(k|k)=\sum _j{P}_j^{\prime }(k|k){\mu }_j(k)$$
其中$P_j^{\prime }(k|k)=P_j(k|k)+[\hat{x}(k|k)-{\hat{x}}_j(k|k)]\times [\hat{x}(k|k)-{\hat{x}}_j(k|k){]}^T$

以上，就是IMM的整个过程。

注：Step3 的结果只用来输出，以及通过状态量只用来更新协方差

3. 示例描述

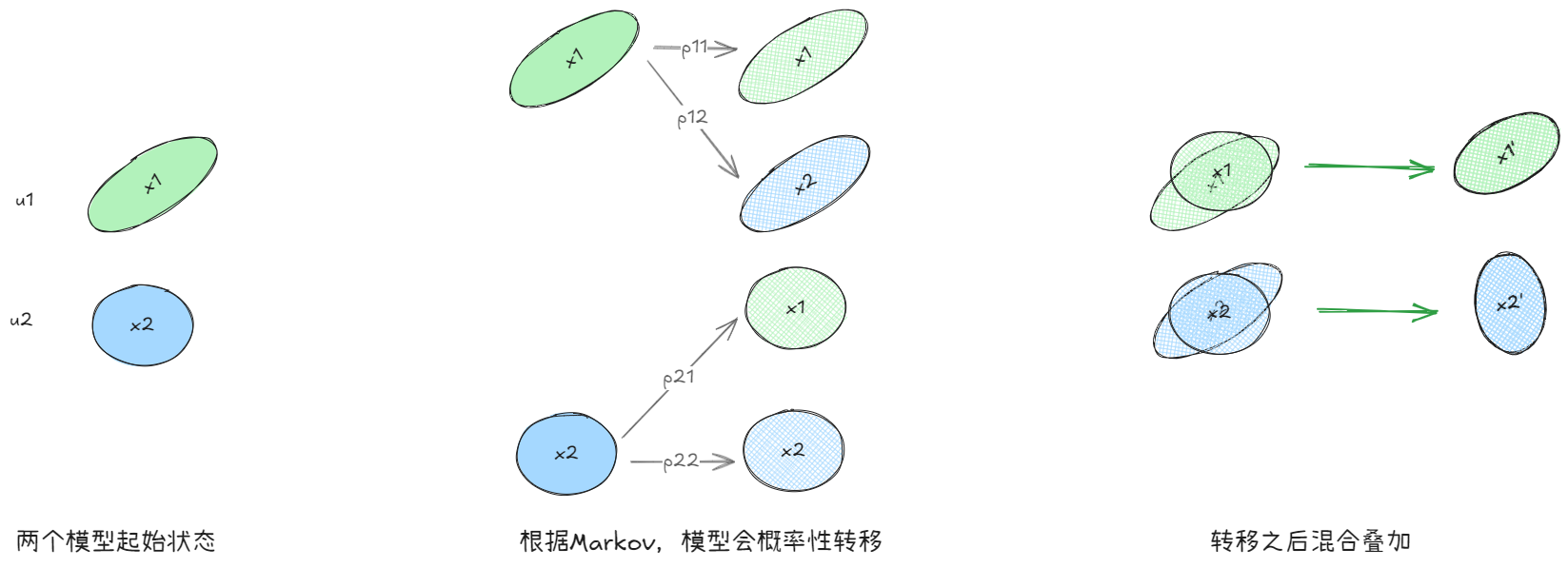
假设我们使用两个模型1和2来对一个观测进行估计，假设两个模型是二维高斯模型，初始状态如下，分别表示两个模型的状态、方差和概率

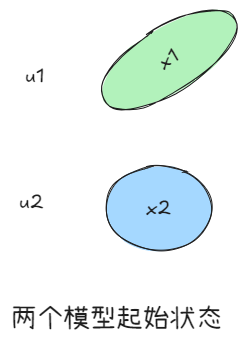
Step1：混合

如图，每个模型都有一定概率转移到另一个模型，我们对转移后的模型态进行混合叠加，在这个过程中，需要更新的变量有：

• 状态量$x$，基于模型概率和转移概率
• 协方差$P$，基于初始协方差和转移叠加后的误差
  

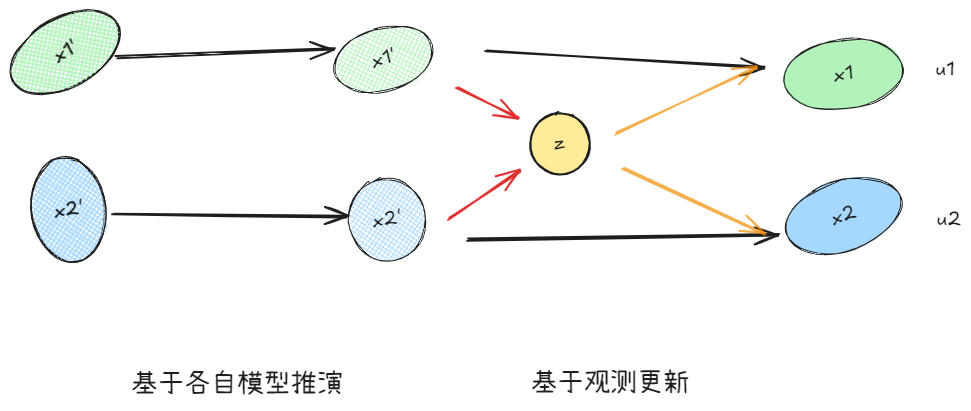
Step2：滤波/更新

如图，基于当前的观测z，分别对两个模型进行更新，这个过程更新的变量包括：

• 状态量$x$，基于模型推演，并根据观测更新
• 协方差$P$，基于推演转移，即观测残差
• 模型概率$\mu$，基于残差的likehood
  

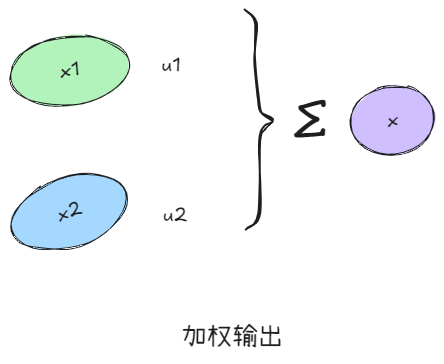
Step3：合并

这一步比较简单，将更新的状态和概率直接加权混合，得到最终输出状态估计值，这个过程中更新的变量包括：

• 状态量$x$，基于加权后的最优估计
• 协方差$P$，基于加权后最优估计与当前模态值的残差

参考文献

[^1] E. Mazor, A. Averbuch, Y. Bar-Shalom and J. Dayan, “Interacting multiple model methods in target tracking: a survey,” in IEEE Transactions on Aerospace and Electronic Systems, vol. 34, no. 1, pp. 103-123, Jan. 1998, doi: 10.1109/7.640267