5.21 note
链表
- 引入虚拟头结点
- 明确指向与计数
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteNodes(ListNode* head, int m, int n)
{
if(m==0) return nullptr;
int cnt=0;
ListNode* newhead=new ListNode(0);
newhead->next=head;
ListNode* pre=newhead;
//!!!!!!!!
while(pre)
{
if(cnt==m)
{
int tmp=n;
ListNode* p=pre->next;
//!!!!!!!!!
while(tmp)
{ if(!p) break;
p=p->next;
tmp--;
}
pre->next=p;
cnt=0;
}
pre=pre->next;
cnt++;
}
return newhead->next;
}
};
二叉树的公共祖先
举例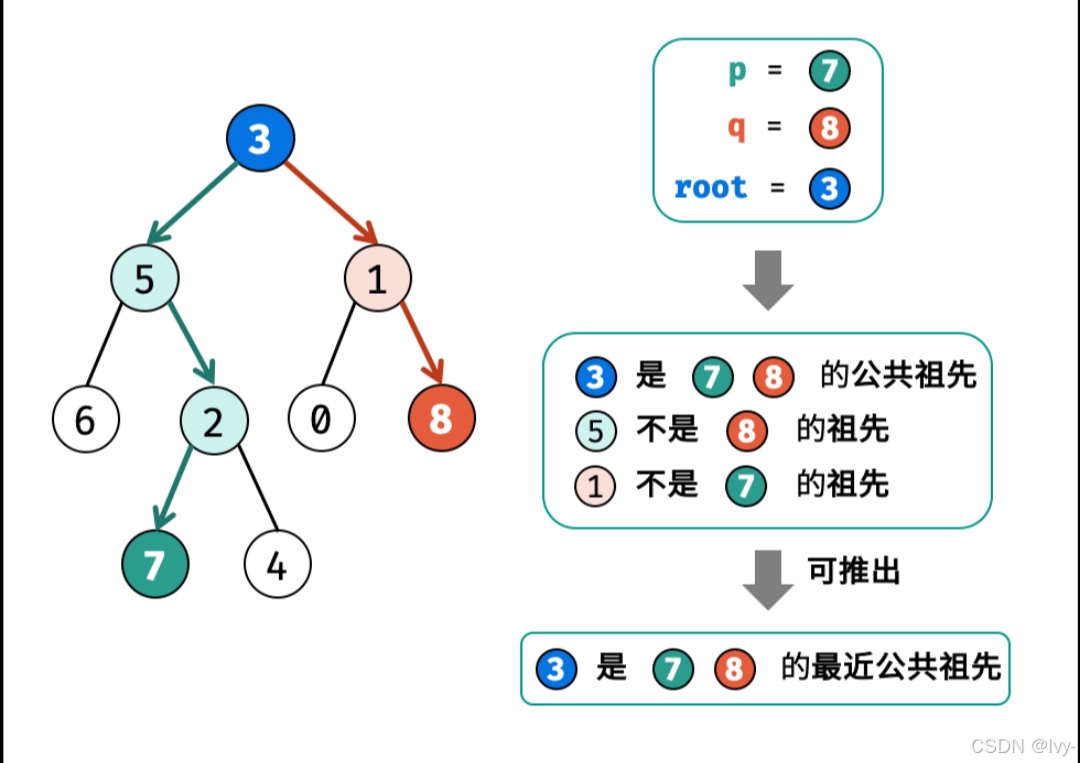
递归思路

代码
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null)
return null;
if(p == root || q == root)
return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left != null && right != null)
return root;
return left == null ? right : left;
}
}
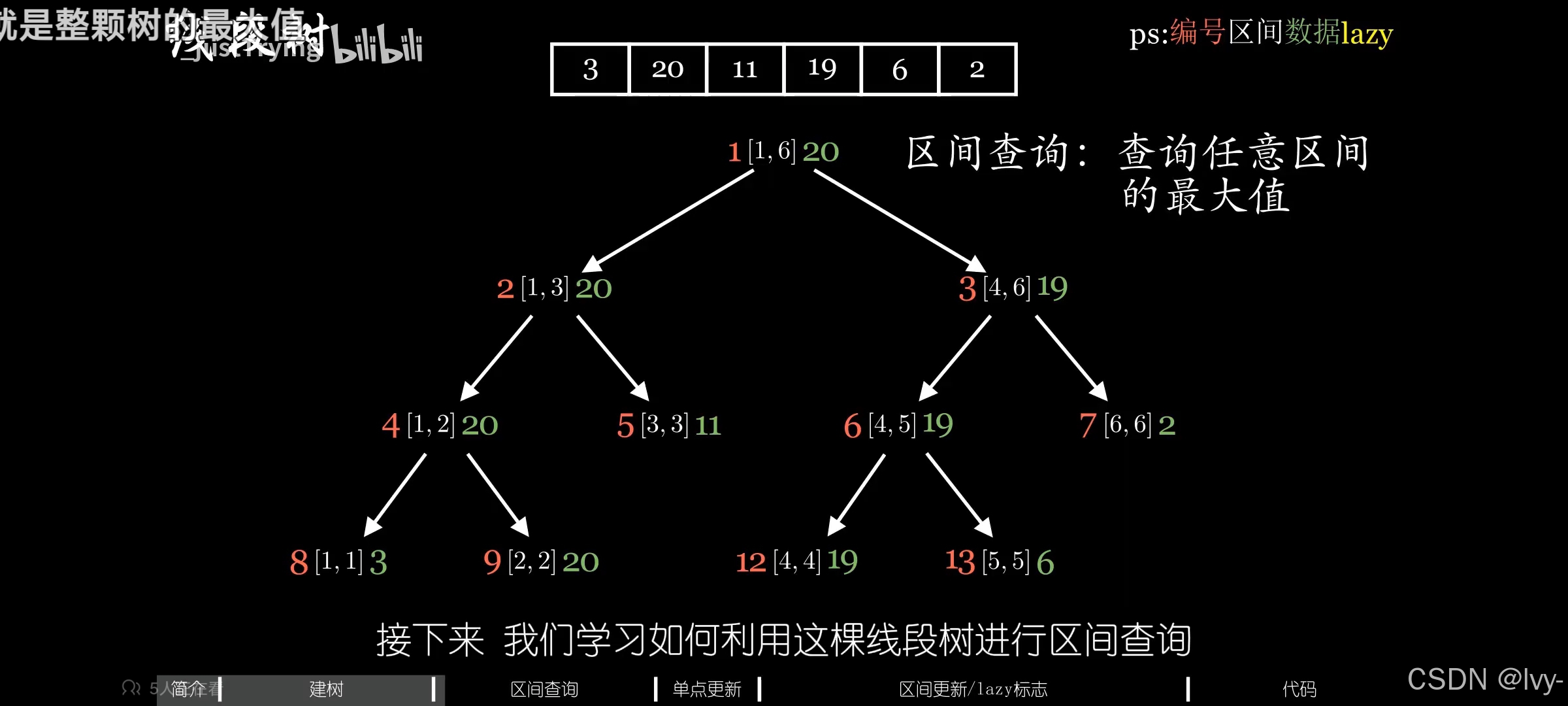
线段树
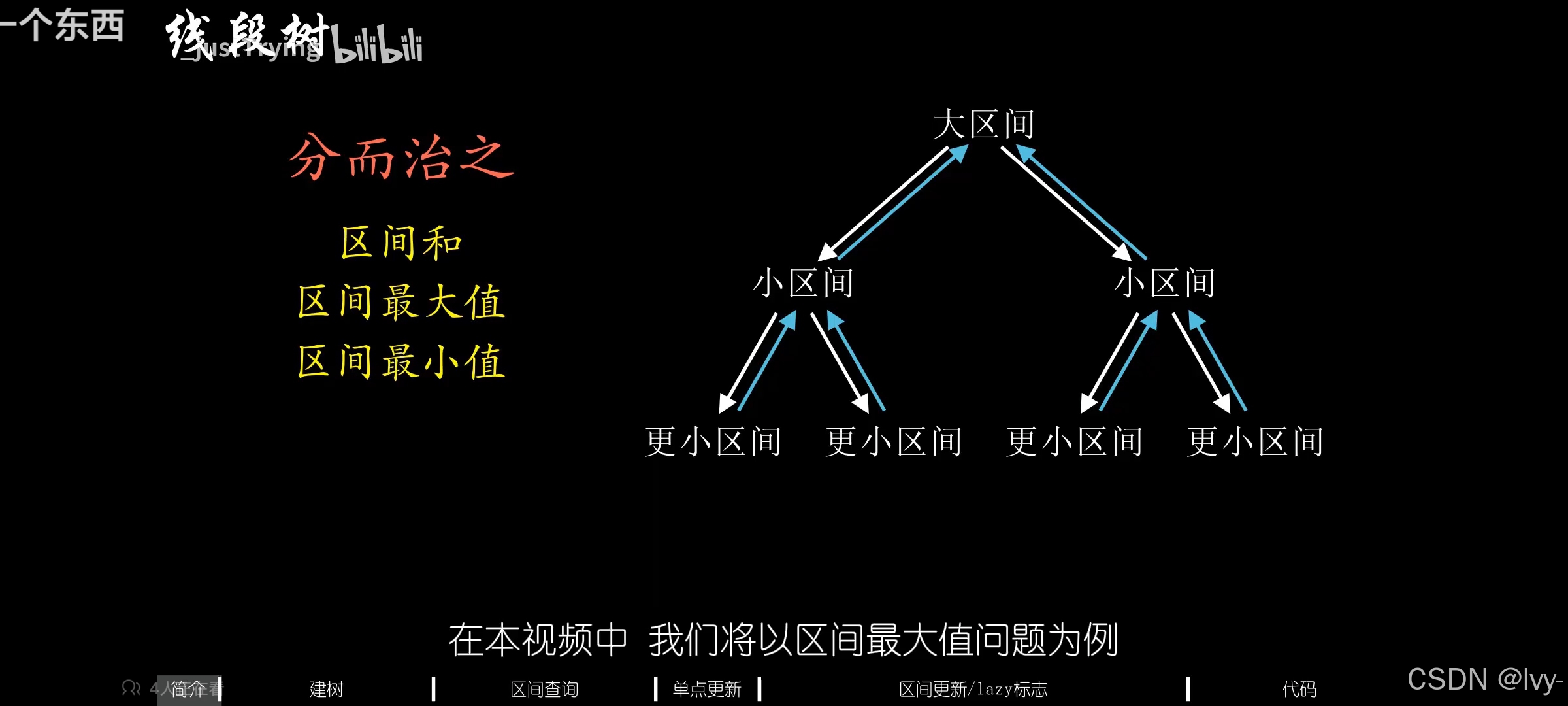
处理
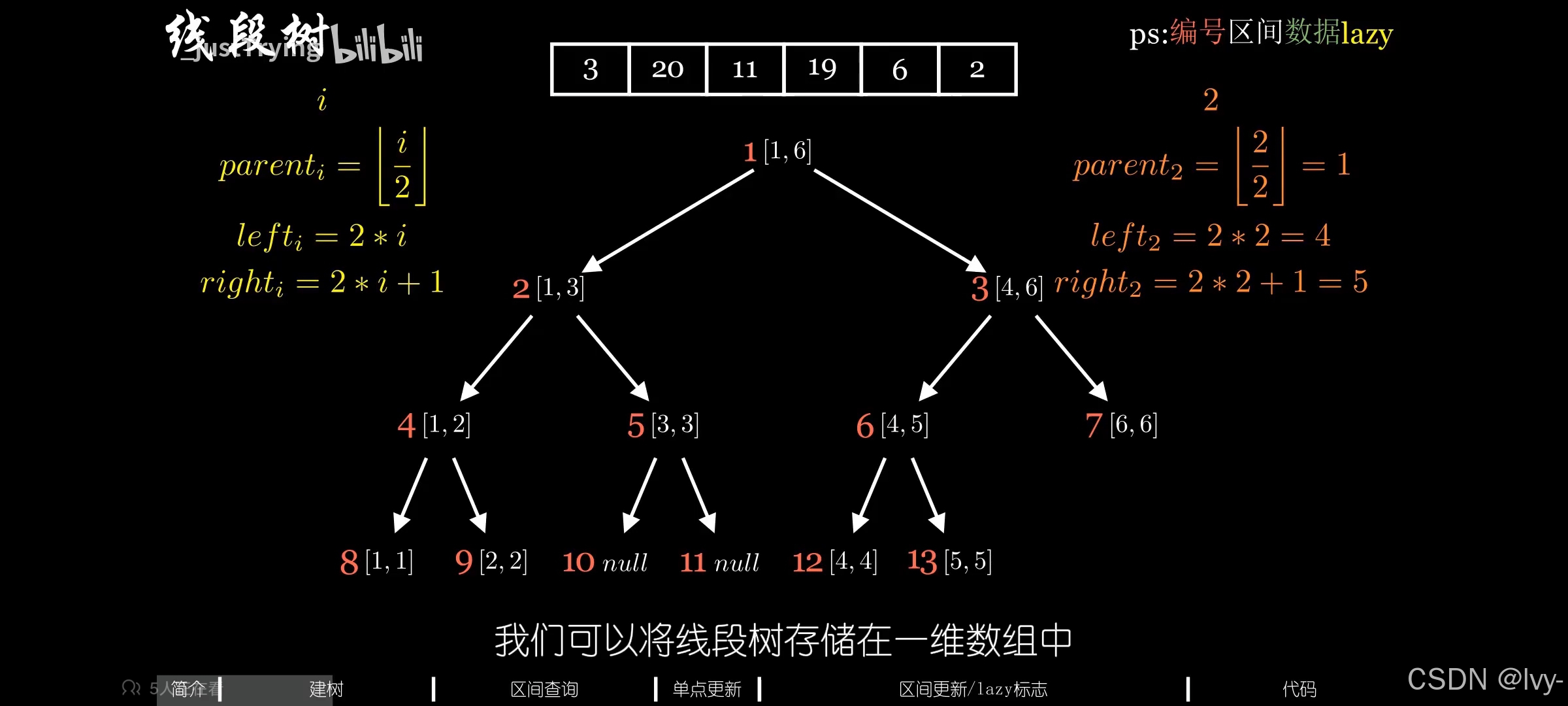
举例
class SegTree {
public:
// 线段树板子开始
SegTree(int n) {
this->n = n;
mx.resize(n << 2);
mn.resize(n << 2);
addTag.resize(n << 2);
change.resize(n << 2);
updateTag.resize(n << 2);
build(1, n, 1);
}
void set(int i, long long v) {
update(i, i, v, 1, n, 1);
}
void add(int l, int r, long long v) {
if (l > r) return;
add(l, r, v, 1, n, 1);
}
long long queryMax(int l, int r) {
if (l > r) return MIN;
return queryMax(l, r, 1, n, 1);
}
private:
static const long long MAX = 0x3f3f3f3f3f3f3f3f;
static const long long MIN = 0;
int n;
std::vector<long long> mx, mn, change, addTag;
std::vector<bool> updateTag;
void up(int i) {
mx[i] = std::max(mx[i << 1], mx[i << 1 | 1]);
mn[i] = std::min(mn[i << 1], mn[i << 1 | 1]);
}
void build(int l, int r, int i) {
if (l == r)
mx[i] = mn[i] = 0;
else {
int mid = (l + r) >> 1;
build(l, mid, i << 1);
build(mid + 1, r, i << 1 | 1);
up(i);
}
updateTag[i] = false;
change[i] = 0;
addTag[i] = 0;
}
void down(int l, int r, int i) {
if (updateTag[i]) {
int mid = (l + r) >> 1;
lazy_update(l, mid, change[i], i << 1);
lazy_update(mid + 1, r, change[i], i << 1 | 1);
updateTag[i] = false;
}
if (addTag[i]) {
int mid = (l + r) >> 1;
lazy_add(l, mid, addTag[i], i << 1);
lazy_add(mid + 1, r, addTag[i], i << 1 | 1);
addTag[i] = 0;
}
}
void lazy_add(int l, int r, long long v, int i) {
mx[i] += v;
mn[i] += v;
addTag[i] += v;
}
void lazy_update(int l, int r, long long v, int i) {
mx[i] = v;
mn[i] = v;
change[i] = v;
updateTag[i] = true;
addTag[i] = 0;
}
void update(int L, int R, long long v, int l, int r, int i) {
if (L <= l && r <= R)
lazy_update(l, r, v, i);
else {
down(l, r, i);
int mid = (l + r) >> 1;
if (L <= mid)
update(L, R, v, l, mid, i << 1);
if (R > mid)
update(L, R, v, mid + 1, r, i << 1 | 1);
up(i);
}
}
void add(int L, int R, long long v, int l, int r, int i) {
if (L <= l && r <= R)
lazy_add(l, r, v, i);
else {
down(l, r, i);
int mid = (l + r) >> 1;
if (L <= mid)
add(L, R, v, l, mid, i << 1);
if (R > mid)
add(L, R, v, mid + 1, r, i << 1 | 1);
up(i);
}
}
long long queryMax(int L, int R, int l, int r, int i) {
if (L <= l && R >= r)
return mx[i];
else {
down(l, r, i);
int mid = (l + r) >> 1;
long long res = MIN;
if (L <= mid)
res = std::max(res, queryMax(L, R, l, mid, i << 1));
if (R > mid)
res = std::max(res, queryMax(L, R, mid + 1, r, i << 1 | 1));
return res;
}
}
};
// 线段树板子结束
class Solution {
public:
int minZeroArray(vector<int>& nums, vector<vector<int>>& queries) {
int n = nums.size();
// 建立起线段树
SegTree seg(n);
for (int i = 1; i <= n; i++) {
// 初始化线段树
seg.set(i, nums[i - 1]);
}
// 提前特判 k == 0 的情况
if (seg.queryMax(1, n) <= 0) {
return 0;
}
for (int i = 0; i < queries.size(); i++) {
int l = queries[i][0], r = queries[i][1], val = queries[i][2];
l++, r++;
// 区间更新
seg.add(l, r, -val);
// 范围查询
if (seg.queryMax(1, n) <= 0) {
return i + 1;
}
}
return -1;
}
};
差分数组
class Solution {
public:
int minZeroArray(vector<int>& nums, vector<vector<int>>& queries) {
int n = nums.size(), m = queries.size();
vector<int> dif(n + 1);
//cur为当前第一个不满足能变到0的数组元素下标
int cur = 0;
//先检查一边,如果初始时就满足的话返回0
while (cur < n && dif[cur] >= nums[cur]) {
cur++;
dif[cur] += dif[cur - 1];
}
if (cur == n) return 0;
for (int i = 0; i < m; i++) {
//如果r < cur, 左边都是已经满足的元素,不用再考虑。
if (queries[i][1] < cur) continue;
//更新差分, 注意左端点是l和cur的max
dif[max(queries[i][0], cur)] += queries[i][2];
dif[queries[i][1] + 1] -= queries[i][2];
//更新cur数组, 注意也要更新dif数组
while (cur < n && dif[cur] >= nums[cur]) {
cur++;
dif[cur] += dif[cur - 1];
}
if (cur == n) {
return i + 1;
}
}
return -1;
}
};
