扩散模型(DDPM)

Diffusion Model(扩散模型)是一种深度学习算法,主要用于生成模型领域,尤其在图像生成中取得了显著的成果。这种模型的核心思想是模拟一个从有序到无序再到有序的扩散过程,通过逐步增加然后再逐步去除噪声的方式来生成数据。
应用:扩散模型在多种数据生成任务中表现出色,例如图像生成、音频合成和文本生成等。在图像生成方面,扩散模型能够生成高质量、高分辨率的图像,竞争力甚至超过了其他类型的生成模型,如生成对抗网络(GANs)。
一、概念
Diffusion model 是如何运作的?
扩散模型包括两个主要的阶段:前向扩散阶段和反向扩散(或去噪)阶段。
前向扩散阶段:在这一阶段,模型将逐步向原始数据添加噪声,使数据从有序状态变成几乎完全随机的噪声状态。这个过程通常是预定的并遵循特定的噪声增加路径。
反向扩散阶段:这一阶段是扩散模型的核心,模型将逐步从噪声数据中恢复出原始的有序数据。在这个过程中,模型学习如何有效地从包含高比例噪声的数据中恢复出干净的数据。这一阶段通常需要通过训练一个深度神经网络来实现。
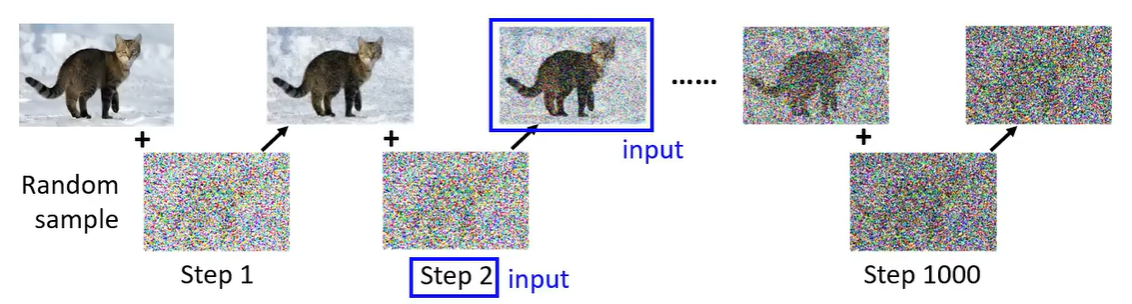
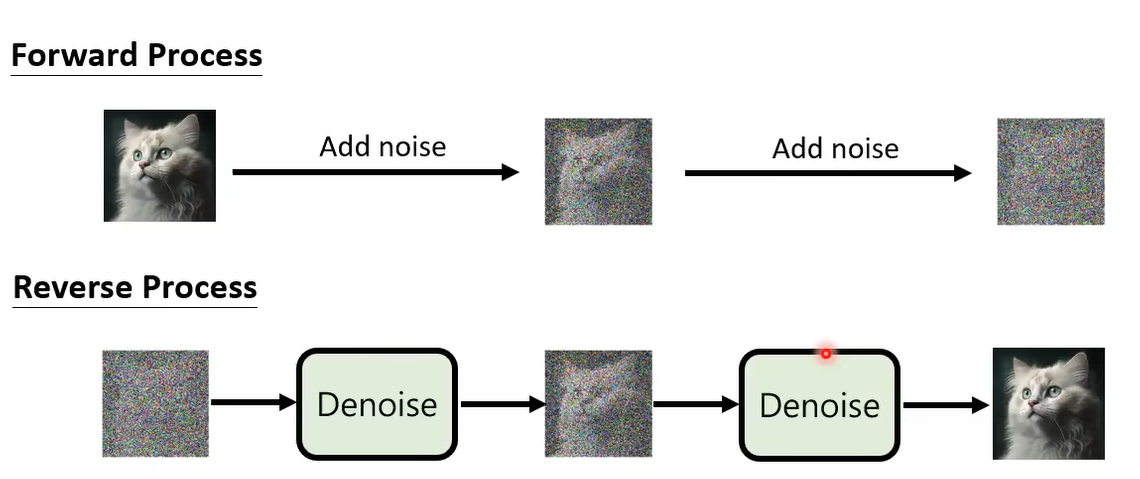
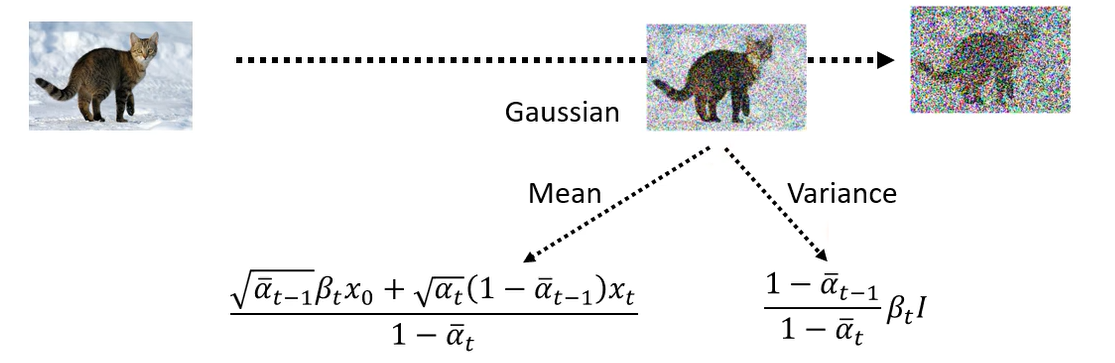
下面是利用 DDPM 生成图片的一个例子。生成图片的过程:从一个高斯分布中采样出一个 vector,这个 vector 的维度跟你想要生成的图片维度大小是一致的,比如 256*256。然后使用一个去噪网络,就会把噪声滤掉一点,就会看到有一个猫的形状。然后再做 denoise,猫的形状逐渐清晰。经过很多步的 denoise 后,就会看到一张清晰的图片。这个 denoise 的次数是实现定好的,我们通常会给每个 denoise 的步骤一个编号,最开始去噪的编号比较大,产生最终图片的编号很小。
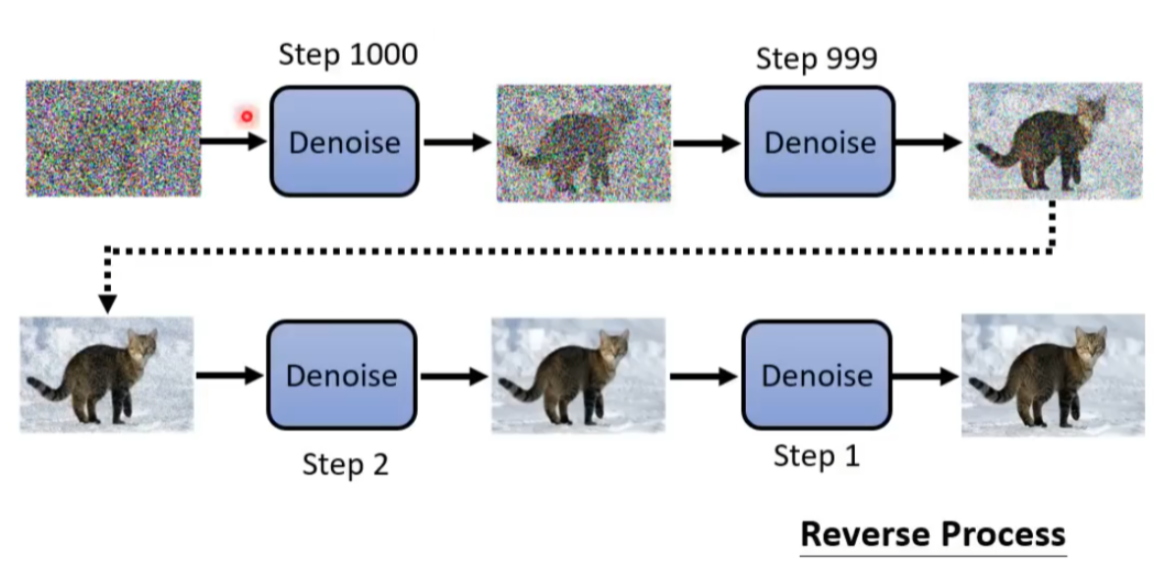
那么从噪声到图片的过程叫做 Reverse Process。在概念上这个事情类似于Michelangelo所说的“The sculpture is already complete within the marble block, before I start my work. It is already there, I just have to chisel away the superfluous material.”雕像本来已经在大理石里面,他只是把不要的部分拿掉。Diffusion model 做的事情是一样的,本来图片就已经在噪声里面,它只是把视为噪声的部分滤掉,就产生一张图片。

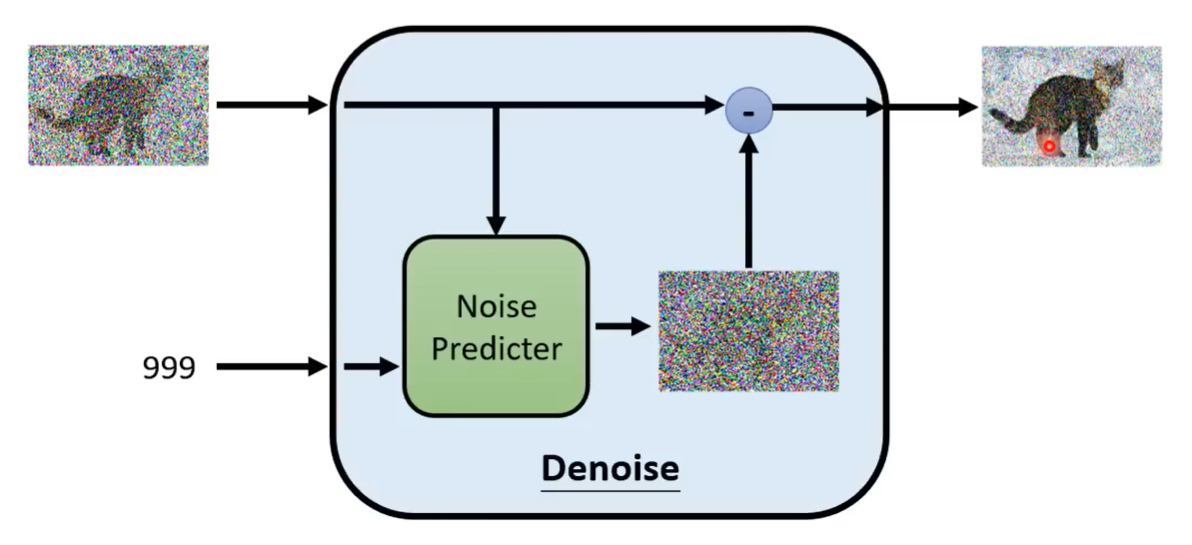
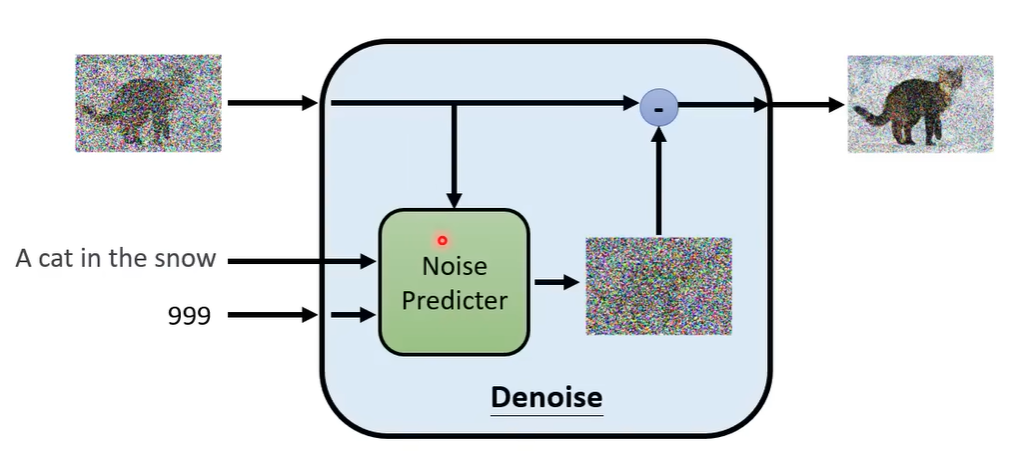
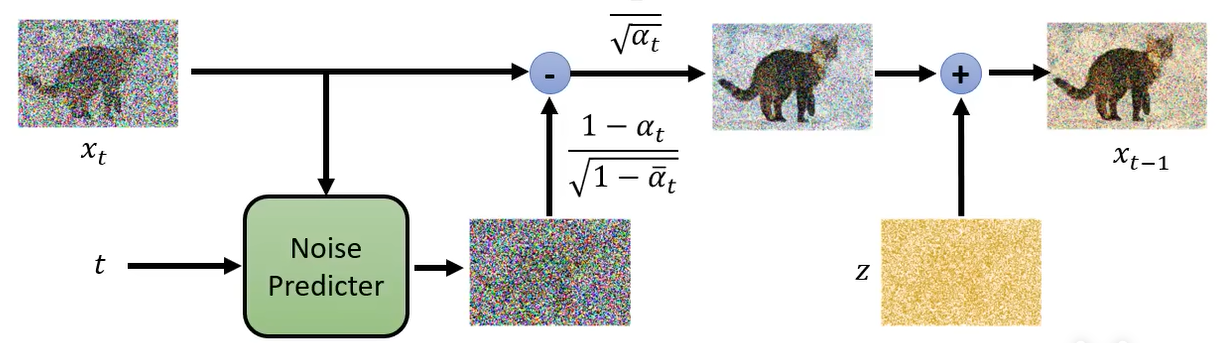
那么,在每一步中都会使用 Denoise model,那么这个 model 是否是同一个呢?答案为是,同一个去噪模型反复使用。但是存在一个问题,因为每个步骤的去噪网络输入的图片差异非常大,比如在1000步,输入的为噪声,在1步中,输入的图片非常接近真实图片。所以同一个模型不一定真的做得很好。所以DDPM提出了一个想法:Denosie 模型除了图片输入以外,还会将目前noise严重程度作为输入,Step 越大表示 noise 越严重。Denosie model 希望根据输入的 Step 做出不同的回应。

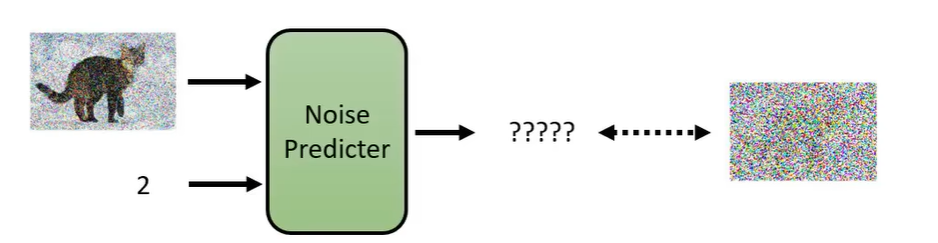
那么 Denoise model 内部实际怎么做的呢?它包含一个 Noise Predictor,它的输入就是噪声图像和Step,其输出就是预测输入图片的噪声。然后使用输入的噪声图像减去预测的噪声就得到下一步的噪声图像。所以 Denoise model 并不是输入一张噪声图像直接输出去噪后的图像。你可能想问,为什么要这么麻烦呢?当然,你也可以这么做。但是多数的论文还是选择先预测噪声,然后相减的方式实现。因为产生一张图片和产生一张噪声的难度是不一样的。如果 Denoise model 已经能够产生一张带噪声的猫,它几乎也能画一只猫了,所以产生带噪声的猫和产生噪声难度区别是很大的。
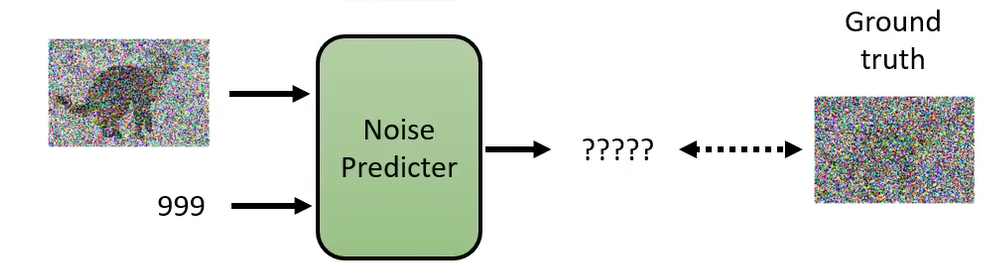
那么怎么训练 Noise Predictor 呢?它的输入是带噪声的图像和 Step,然后输出是噪声。那么我们训练的时候,就需要知道这个真实的噪声(Ground Truth)到底长什么样子。那么我们怎么创建训噪声样本对呢?
创建方法如下:选择一张干净的图片,然后我们自己加噪声,比如说从高斯分布中采样一个纯噪声的vecotor,产生一张优点噪声的图片;在sample一次,得到更多噪声的图片,一次类推,最后得到纯噪声图像。把所有的图片都进行这样的一个加噪过程,那么这个过程就叫做 Forward Process(Diffusion Process)。
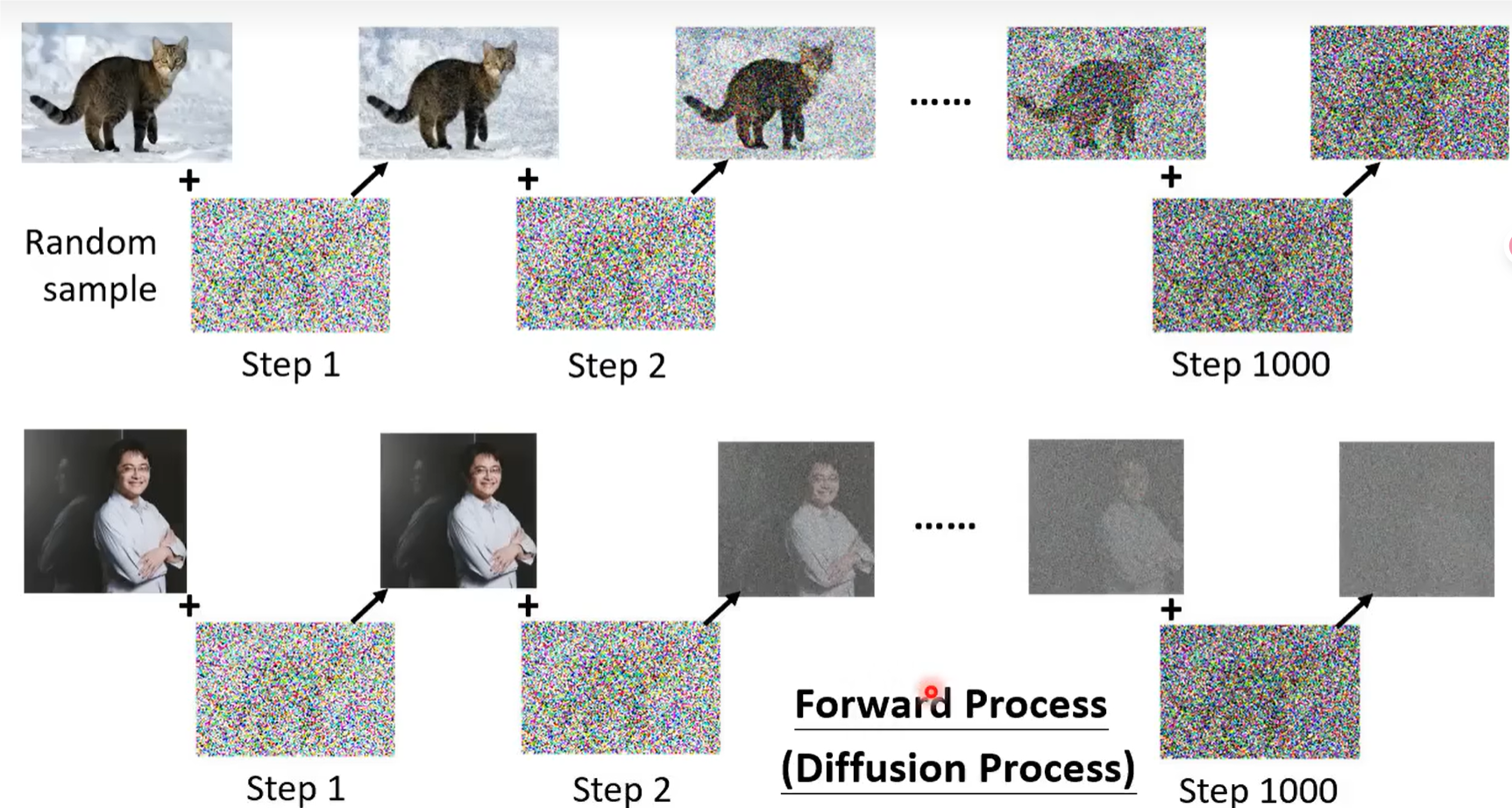
做完这个步骤后,我们就拿到了 Noise Predictor 的训练数据,也就是加完噪声后的图像和现在是第几次加入噪声,也就是 Noise Predictor 的输入。那么加入的噪声就是 Noise Predictor 的输出的 ground truth。
那么对于 Noise Predictor 来说,看到这张噪声图像,Step=2,那么你期望的输出就是第2步所加的噪声。然后向普通的神经网络一样,一直训练下去。
上面只能实现从噪声中产生图像,如果我们想要输入一段文字然后产生对应的图像,这个怎么做呢?

如果我们想要训练上面这个文本到图像的生成器的话,依然需要成对的训练数据。那需要多少训练数据呢?目前很流行的一些文本到图像的扩散模型使用了 LAION 这个训练集,包括 58.5亿个数据,这也是它们为什么产生如此好的结果的原因。这个网络不仅仅是图像对应的英文,还有中文,日文的对应。所以目前的一些影像生成的模型你不管输入什么语言都能够识别。那么这些就是需要准备的训练数据。
在这种情况下,我们直接将文字也作为 Denoise model 的输入即可。
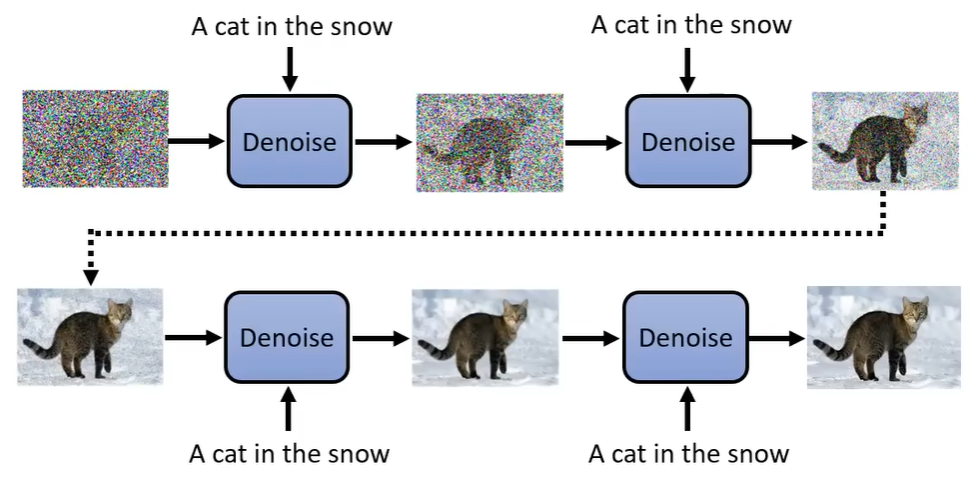
那么 Noise Predictor 多了一个额外的文字输入。
二、数学原理
回顾一下扩散模型的整个流程。
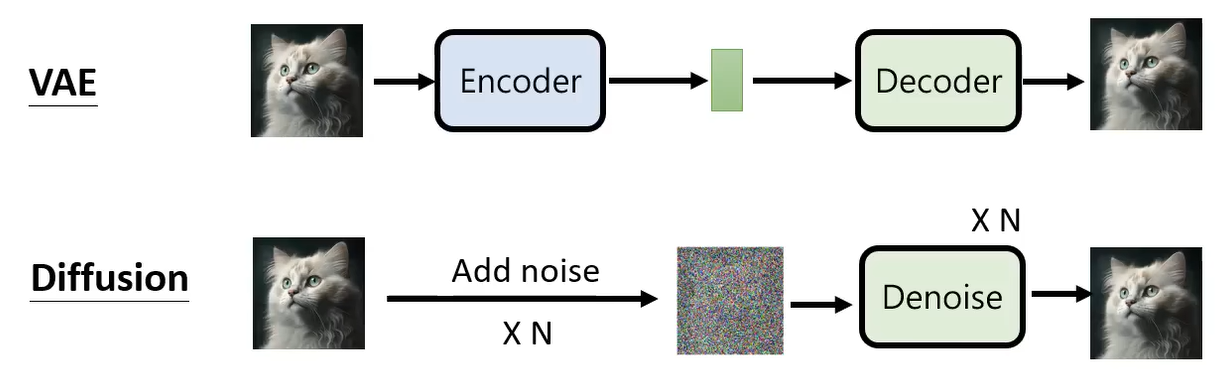
Diffusion model 和 VAE(Variational AutoEncoder)其实比较类似,VAE 就是先使用一个 Encoder 把一张图片变成一个隐式表示,然后将这个隐式表示还原为原始图片。对于 Diffusion 来说,可以想象成加噪的过程就是 Encoder 的过程,只是这个 Encoder 不是一个神经网络,不是学习出来的。加噪的过程是固定的,不需要学习。通过加N次噪声,图片变成只有噪声的图像,这个就相当于 VAE 的隐式表示;那么 Denoise 相当于 VAE 当中的 decoder,将纯噪声图像还原为原始图像。
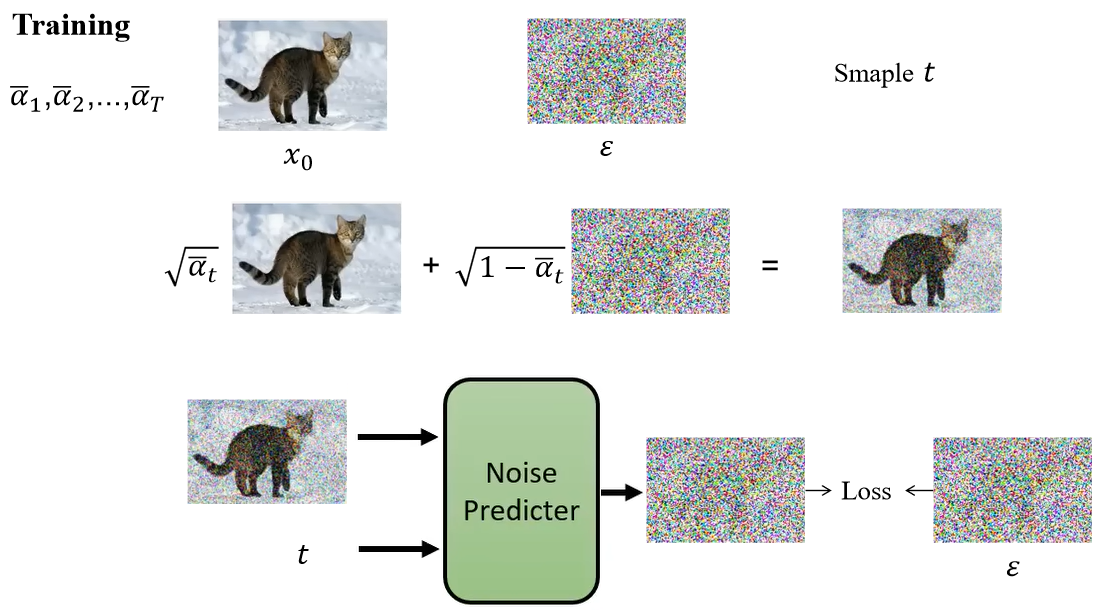
Diffusion model 的训练过程如下:首先,取出一张干净的图像(也就是我们最后要生成的图像);然后再从1-T(T为一个比较大的数字,比如1000)的时间步范围内取出一个 Step t;从正态分布中采样一个 vector(噪声,与图像维度相同)。


在第五行中,先将 x 0 x_0 x0 和 ϵ \epsilon ϵ 做一个加权和,这个权重 α ˉ 1 , α ˉ 2 , ⋯ , α ˉ T \bar{\alpha}_1, \bar{\alpha}_2, \cdots, \bar{\alpha}_T αˉ1,αˉ2,⋯,αˉT (通常由大到小,递减)是事先定义好的。它们经过加权和后得到的就是一张含有噪声的图像。当 t t t 越大, α ˉ t \bar{\alpha}_t αˉt 越小,那么加的噪声就越多。得到含噪声图像后,将其和 t t t 一起作为 ϵ θ \epsilon_{\theta} ϵθ 的输入,也就是 Noise Predictor,然后输出一个预测的噪声图像,与真实的噪声图像 ϵ \epsilon ϵ 计算损失。可以用下面流程表示:
Diffusion model 的推理过程如下:首先 sample 一个 噪声图像 x T \mathbf{x}_T xT。然后这个过程需要迭代 T 次。然后这里有一个疑问?每一次循环的时候,为什么会先从正态分布中再 sample 一个 噪声 z \mathbf{z} z。
在第 4 行中, x t \mathbf{x}_t xt 表示上一步生成的噪声图像, ϵ θ ( x t , t ) \epsilon_{\theta}(\mathbf{x}_t, t) ϵθ(xt,t) 为 Noise Predictor 在 Step= t t t 预测的噪声。这里有一个令人匪夷所思的操作,为什么最后还要添加一个噪声?所以说 DDPM 的算法是暗藏玄机的。

公式来源要从影像生成模型本质上的共同目标为:输入有一个简单的分布(比如高斯分布),从分布中 sample 一个 vector;然后将 vector 输入到网络中,然后生成 x x x(这里表示一张图片)。那么我们每 sample 一个 vector,都会生成一张图片。
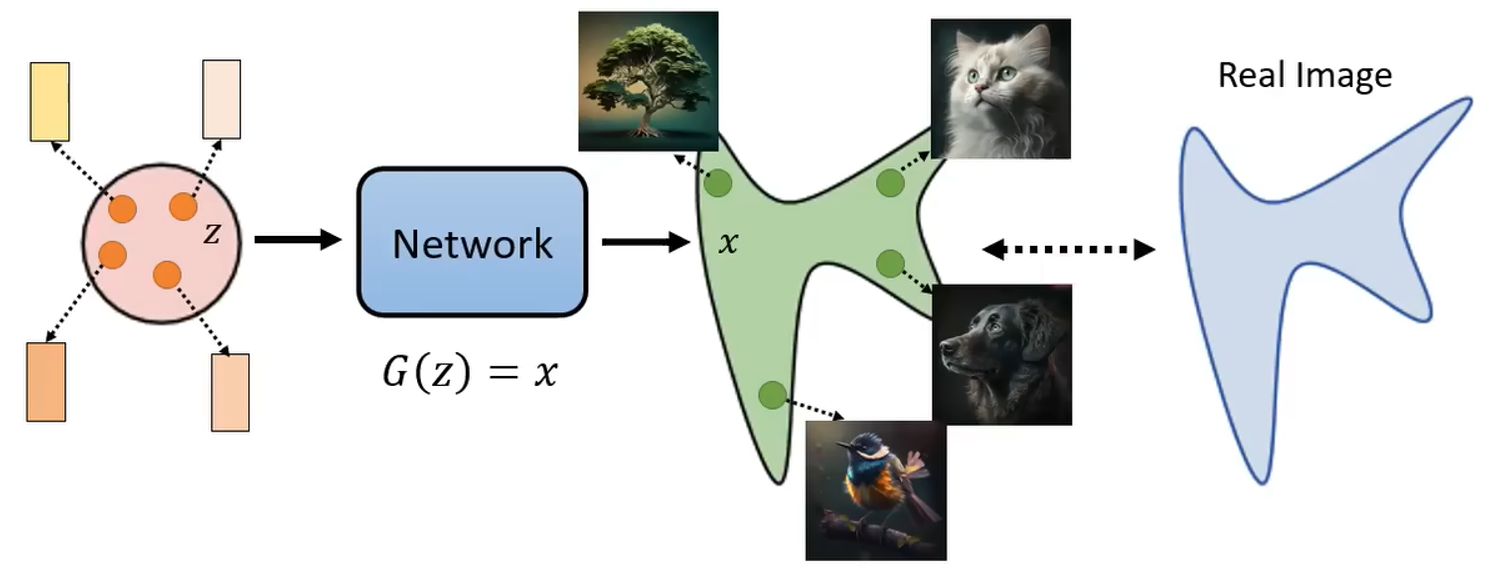
就算是一个非常简单的高斯分布,通过网络的转换都会变成一堆图片。图片会组合成非常复杂的分布。我们期望的是找到一个网络,使得生成图片的分布和真实图片的分布越接近越好。这就是影像生成模型本质上的共同目标。
那么我们怎么衡量两个分布越接近越好?大多数模型都采取的是最大似然估计。假设网络的参数为 θ \theta θ,根据网络生成的数据的分布为 P θ ( x ) P_{\theta}(x) Pθ(x),真正的数据分布为 P d a t a ( x ) P_{data}(x) Pdata(x)。
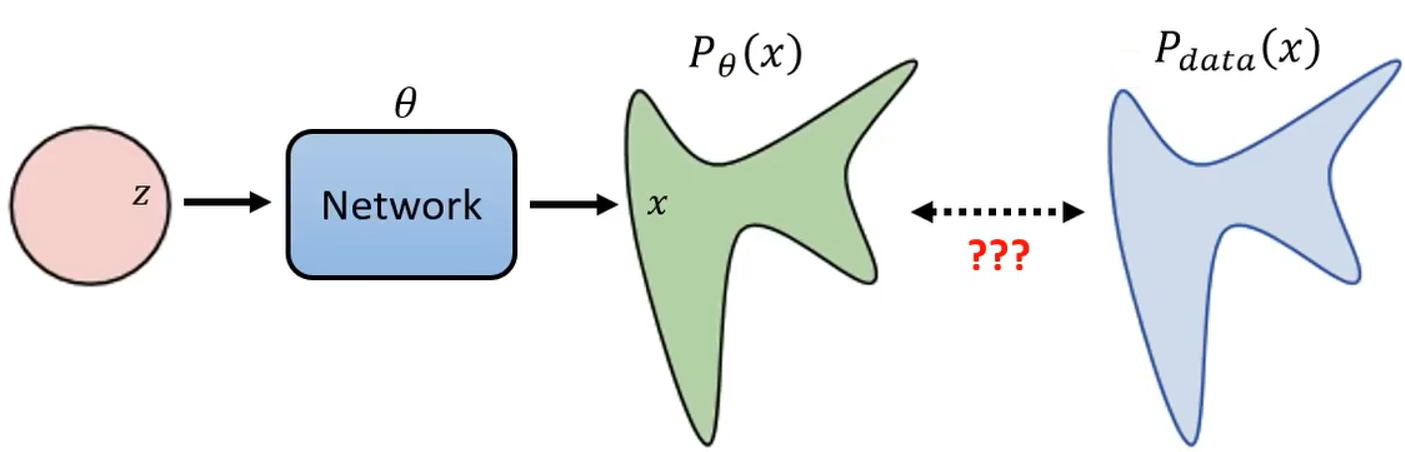
首先我们从真实图片 P d a t a ( x ) P_{data}(x) Pdata(x) 中选取一组图片 x 1 , x 2 , . . . , x m x^1, x^2, ..., x^m x1,x2,...,xm。这里假设我们可以计算 P θ ( x i ) P_{\theta}(x^i) Pθ(xi),通过网络产生的概率分布为 P θ P_{\theta} Pθ,假设随机给一张图片 x i x^i xi,我们都可以算 P θ P_{\theta} Pθ 产生 x i x^i xi 的概率。这个假设实际上可能是没法做到的,因为 P θ P_{\theta} Pθ 这个分布非常的复杂。但是没有关系,这里先假设可以计算 P θ ( x i ) P_{\theta}(x^i) Pθ(xi)。那么我们需要寻找一个 θ \theta θ 可以让选取的图片产生出来的概率最大。也就是找到一个 θ \theta θ,能出现真实数据的概率最大。
θ ∗ = a r g max θ ∏ i = 1 m P θ ( x i ) \theta^* = arg \max_{\theta} \prod_{i=1}^m P_{\theta}(x^i) θ∗=argθmaxi=1∏mPθ(xi)
为什么 x 1 , x 2 , . . . , x m x^1, x^2, ..., x^m x1,x2,...,xm 这些图片产生的概率越大越好,就是使得两个分布越来越接近。这两者之间的关联是什么?

首先,先取一个对数,这个不会影响最终找出的结果。log 相乘等于相加取 log。然后这个式子可以近似于我们从 P d a t a P_{data} Pdata 里面取 x x x 出来,然后计算 log P θ ( x ) \log P_{\theta}(x) logPθ(x) 的期望值。这里使用的是大数定律,当样本 m m m 趋于无穷时,样本均值趋近于总体分布的期望。然后这个式子可以写做对这个式子做积分,然后它这里减去了一个积分,这个积分毫无用处,因为与 θ \theta θ 无关,所以不会影响结果。 这一项只跟真实图像有关。但是这样做的好处是可以将两项进行合并,那么合并后的式子(注意有一个负号)就是 P d a t a P_{data} Pdata 和 P θ P_{\theta} Pθ 这两个分布的 KL散度。KL散度就是计算两个分布之间的差异,值越大表示两个分布差异越大。那么 “最大似然估计 = 最小化 KL 散度”。
下面先看一下 VAE 是怎么计算 P θ ( x ) P_{\theta}(x) Pθ(x),因为 DDPM 很多原理和它类似。我们从高斯分布中 sample 出的 vector 经过网络所形成的分布 P θ ( x ) P_{\theta}(x) Pθ(x)。
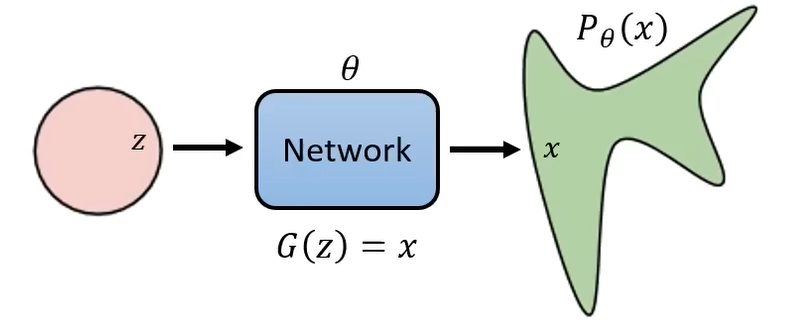
如果我们想要定义 P θ ( x ) P_{\theta}(x) Pθ(x),可以写成:
P θ ( x ) = ∫ z P ( z ) P θ ( x ∣ z ) d z P_{\theta}(x) = \int_z P(z)P_{\theta}(x|z) \mathrm{d}z Pθ(x)=∫zP(z)Pθ(x∣z)dz
我们要算 x x x 被产生出来的概率,那么每一个 z z z 产生的概率,然后再看每一个 z z z 产生 x x x 的几率,然后再对所有的 z z z 进行积分,就是生成 x x x的概率。每一个 z z z 产生的概率可以得到,因为是从简单的高斯分布中sample的。那么 P θ ( x ∣ z ) P_{\theta}(x|z) Pθ(x∣z) 怎么定义呢?可以写作
P θ ( x ∣ z ) = { 1 , if G ( z ) = x 0 , if G ( z ) ≠ x P_{\theta}(x \mid z) = \begin{cases} 1, & \text{if } G(z) = x \\ 0, & \text{if } G(z) \neq x \end{cases} Pθ(x∣z)={1,0,if G(z)=xif G(z)=x
但是这样定义的缺点是可能几乎都是 0,因为很难生出两张图片一模一样,那有什么办法呢?在VAE里面,采用了如下的办法: 网络假设数据 x x x 的条件分布 P θ ( x ∣ z ) P_{\theta}(x \mid z) Pθ(x∣z) 服从 G ( z ) G(z) G(z) 为均值的高斯分布,表示为 P θ ( x ∣ z ) = N ( x ; G ( z ) , σ 2 I ) P_{\theta}(x \mid z) = \mathcal{N}(x; G(z), \sigma^2I) Pθ(x∣z)=N(x;G(z),σ2I)。
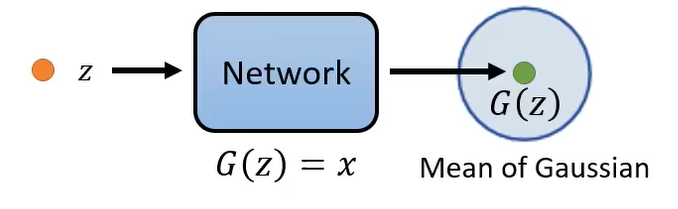
根据高斯分布的概率密度函数,其表达式为:
P θ ( x ∣ z ) ∝ exp ( − ∣ ∣ G ( z ) − x ∣ ∣ 2 2 σ 2 ) P_{\theta}(x \mid z) \propto \exp(- \frac{||G(z) - x||_2}{2\sigma^2}) Pθ(x∣z)∝exp(−2σ2∣∣G(z)−x∣∣2)
VAE 的生成模型假设数据 x x x 由潜在变量 z z z 通过生成器 G ( z ) G(z) G(z) 映射到数据空间,并叠加高斯噪声生成,因此 x x x 的概率密度与生成结果 G ( z ) G(z) G(z) 和真实数据 x x x 之间的欧式距离平方(||G(z) - x||_2)负相关。当方差为常数则可简化为 P θ ( x ∣ z ) ∝ exp ( ∣ ∣ G ( z ) − x ∣ ∣ 2 ) P_{\theta}(x \mid z) \propto \exp(||G(z) - x||_2) Pθ(x∣z)∝exp(∣∣G(z)−x∣∣2)。
那么我们通常在计算 VAE 时,没有办法直接最小化 log P ( x ) \log P(x) logP(x),而是通过最小化 log P ( x ) \log P(x) logP(x) 的下界。其目标时通过变分推断将难以计算的边缘似然 log P θ ( x ) \log P_{\theta}(x) logPθ(x) 转化为可优化的下界。首先,我们的目标是计算真实图像 x x x 的对数似然 log P θ ( x ) \log P_{\theta}(x) logPθ(x),直接计算需要对 z z z 进行积分:
log P θ ( x ) = log ∫ z P θ ( x , z ) d z \log P_{\theta}(x) = \log \int_z P_{\theta}(x, z) \mathrm{d}z logPθ(x)=log∫zPθ(x,z)dz
这个积分在高维空间 ( z z z 维度高) 中难以解析求解。
因此,我们引入一个近似后验分布 q ( z ∣ x ) q(z|x) q(z∣x)(由编码器网络参数化),用于逼近真实后验 P θ ( z ∣ x ) P_{\theta}(z \mid x) Pθ(z∣x)。(贝叶斯定理)

这样就转换成可以去最大化这个下界。其中 q ( z ∣ x ) q(z|x) q(z∣x) 就是 VAE 的 encoder。
那么我们怎么计算 DDPM 的 P θ ( x ) P_{\theta}(x) Pθ(x) 呢?

与 VAE 类似,这里也把 Denoise 的结果看作时高斯分布的均值。那么也存在 P θ ( x t − 1 ∣ x t ) ∝ exp ( − ∣ ∣ G ( x t ) − x t − 1 ∣ ∣ 2 ) P_{\theta}(x_{t-1} \mid x_t) \propto \exp(- ||G(x_t) - x_{t-1}||_2) Pθ(xt−1∣xt)∝exp(−∣∣G(xt)−xt−1∣∣2)
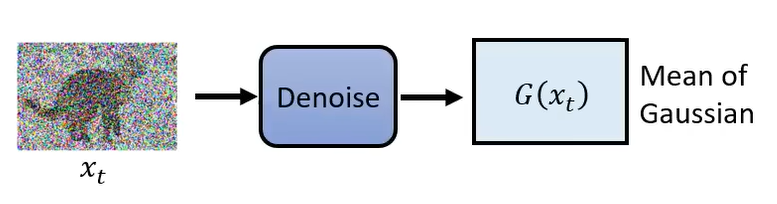
DDPM产生某一张图片 x 0 x_0 x0 的概率可以定义为
P θ ( x 0 ) = ∫ x 1 : x T P ( x T ) P θ ( x T − 1 ∣ x T ) . . . P θ ( x t − 1 ∣ x t ) . . . P θ ( x 0 ∣ x 1 ) d x 1 : x T P_{\theta}(x_0) = \int_{x_1:x_T} P(x_T)P_{\theta}(x_{T-1}|x_T) ... P_{\theta}(x_{t-1}|x_t)...P_{\theta}(x_0|x_1) \mathrm{d}_{x_1:x_T} Pθ(x0)=∫x1:xTP(xT)Pθ(xT−1∣xT)...Pθ(xt−1∣xt)...Pθ(x0∣x1)dx1:xT
它是对所有可能的 x T x_T xT 到 x 1 x_1 x1 做积分,积分内容为 x T x_T xT 产生的概率乘上 x T x_T xT 的基础上产生 x T − 1 x_{T-1} xT−1 产生的概率,一直乘到 x 1 x_1 x1 的基础上产生 x 0 x_0 x0 的概率,就是 x 0 x_0 x0 产生的概率。
那么 DDPM 的 log P ( x ) \log P(x) logP(x) 的下界与 VAE 类似。将 x x x 替换为 x 0 x_0 x0, z z z 替换为 x 1 : x T x_1:x_T x1:xT。
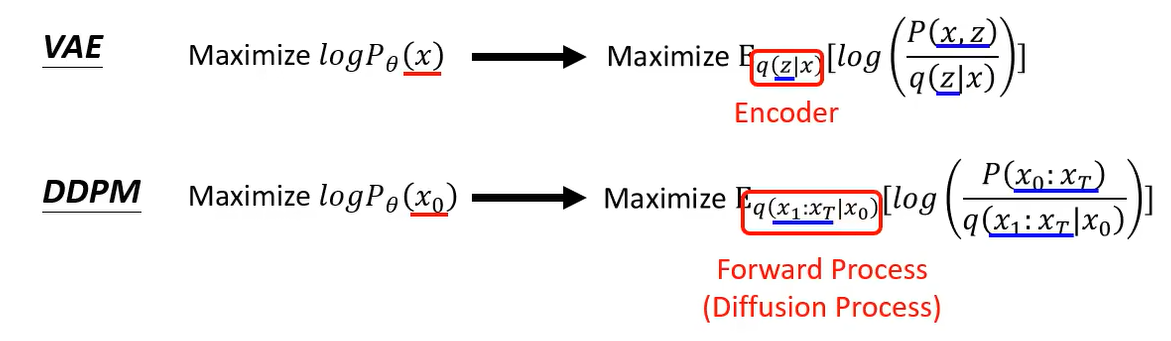
其中 VAE 中的 q q q 表示 Encoder,DDPM 的 q q q 表示加噪过程,表示为:
q ( x 1 : x T ∣ x 0 ) = q ( x 1 ∣ x 0 ) q ( x 2 ∣ x 1 ) . . . q ( x T ∣ x T − 1 ) q(x_1:x_T \mid x_0) = q(x_1 \mid x_0) q(x_2 \mid x_1) ... q(x_T \mid x_{T-1}) q(x1:xT∣x0)=q(x1∣x0)q(x2∣x1)...q(xT∣xT−1)
那么应该怎么计算 q ( x t ∣ x t − 1 ) q(x_t \mid x_{t-1}) q(xt∣xt−1) 呢?首先有一张图 x t − 1 x_{t-1} xt−1,前面乘上 1 − β t \sqrt{1 - \beta_t} 1−βt,这个 β t \beta_t βt( β 1 \beta_1 β1, β 2 \beta_2 β2, … β T \beta_T βT)是预先定义好的值。再加上 β t \sqrt{\beta_t} βt 乘上从高斯分布 sample 的一个噪声。
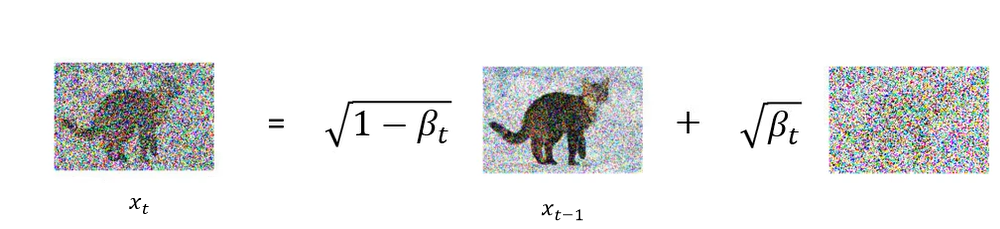
所以 q ( x t ∣ x t − 1 ) q(x_t \mid x_{t-1}) q(xt∣xt−1) 这个分布其实是一个均值为 1 − β t x t \sqrt{1 - \beta_t} x_t 1−βtxt,方差为 β t \beta_t βt 高斯分布。
那么怎么计算 q ( x t ∣ x 0 ) q(x_t \mid x_0) q(xt∣x0) 呢?你可能认为如下图所示,有了 x 0 x_0 x0,再产生 x 1 x_1 x1,再产生 x 2 x_2 x2,直到产生 x t x_t xt,就可以算出 q ( x t ∣ x 0 ) q(x_t \mid x_0) q(xt∣x0) 的概率。

其实 q ( x t ∣ x 0 ) q(x_t \mid x_0) q(xt∣x0) 的概率是可以直接被算出来的。 x 1 x_1 x1 和 x 2 x_2 x2 所添加的噪声是独立的。
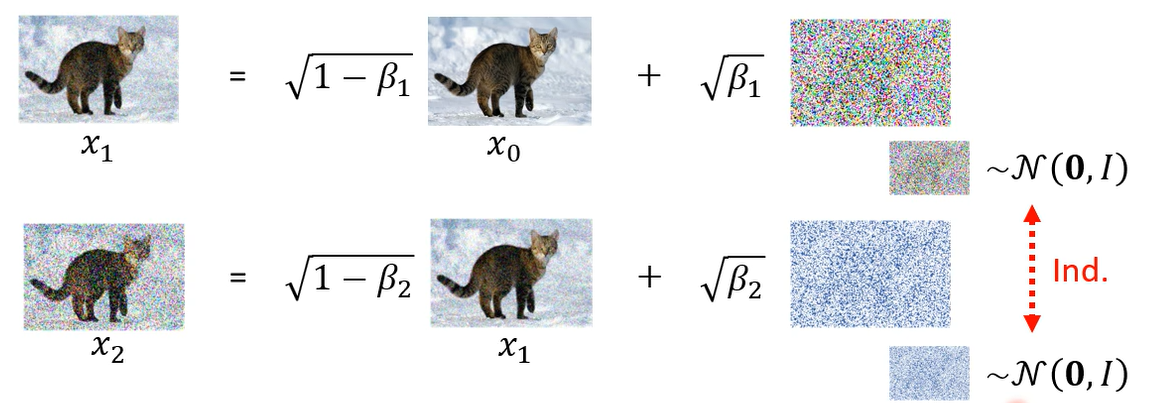
那么我们可以把 x 1 x_1 x1 带入到 x 2 x_2 x2 中。

我们发现,从同一个高斯分布 sample 两次然后再乘上两个不同的权重加起来的分布可以把它简化成只 sample 一次,然后乘上另外一个不同的权重。那么可以得到 x 2 x_2 x2 和 x 0 x_0 x0 之间的关系。

以此类推,从 x 0 x_0 x0 到 x 1 x_1 x1,从 x 1 x_1 x1 到 x 2 x_2 x2,直到 x t − 1 x_{t-1} xt−1 到 x t x_t xt。整个过程可以全部合起来。

这里为了简化符号,将 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt, α ˉ t = α 1 α 2 ⋯ α t \bar{\alpha}_t=\alpha_1\alpha_2 \cdots \alpha_t αˉt=α1α2⋯αt,然后最终表示为:
x t = α t ˉ x 0 + 1 − α t ˉ ϵ x_t = \sqrt{\bar{\alpha_t}} x_0 + \sqrt{1- \bar{\alpha_t}} \epsilon xt=αtˉx0+1−αtˉϵ
那么 DDPM 的目标计算如下所示(看不懂直接跳过):

总之经过一番推导后,得到一个最终的目标。
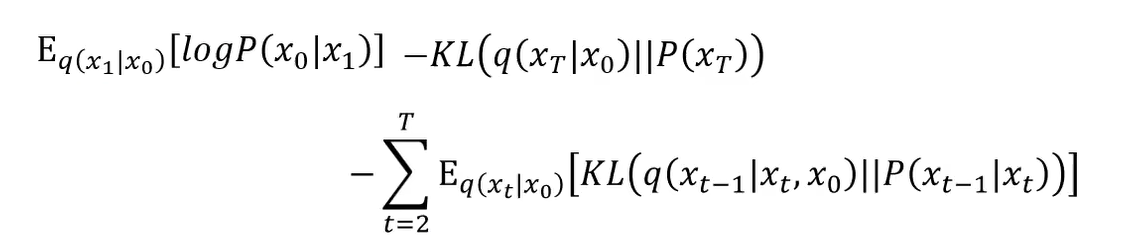
总共有三项。第一项为从 x 1 x_1 x1 重构原始数据 x 0 x_0 x0 的对数似然期望。第二项可以不用管( q q q 是前向传播加噪声的过程),它和网络参数是无关的。第三项的 P ( x t − 1 ∣ x t ) P(x_{t-1}|x_t) P(xt−1∣xt) 是与网络相关的。其中第一项的计算过程与第三项类似。
之前我们已经计算了下图中的分布。
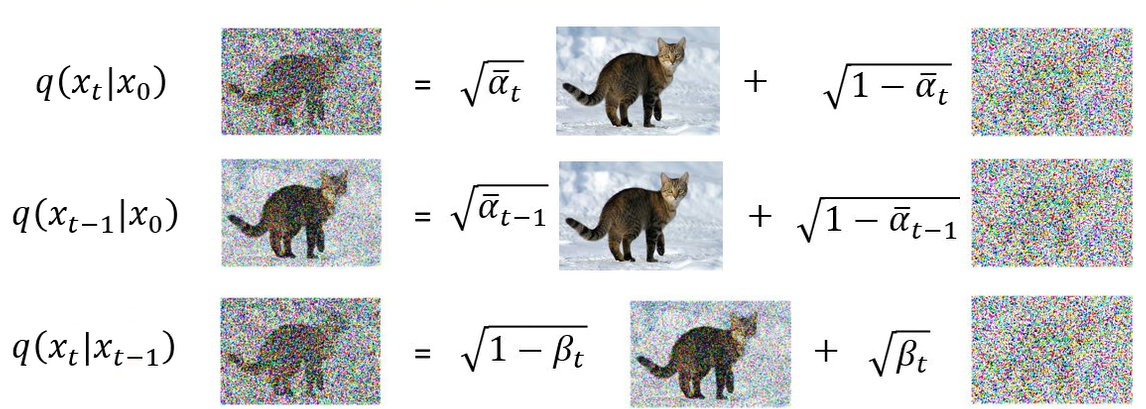
那么怎么计算 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0) 呢?这一项的含义为已知 x 0 和 x t x_0 和 x_t x0和xt,求出 x t − 1 x_{t-1} xt−1 的分布。假设我们已经看到 x 0 x_0 x0,然后做了 t t t 次的 Diffusion 得到了 x t x_t xt。但是中间的过程是未知。然后问你 x t − 1 x_{t-1} xt−1 的分布。所以它不是单纯说给你 x 0 x_0 x0 来求 x t − 1 x_{t-1} xt−1 的分布,这是会算的。

这里我们会算 q ( x t ∣ x 0 ) , q ( x t − 1 ∣ x 0 ) 和 q ( x t ∣ x t − 1 ) q(x_t \mid x_0), q(x_{t-1} \mid x_0) 和 q(x_t \mid x_{t-1}) q(xt∣x0),q(xt−1∣x0)和q(xt∣xt−1)。那么我们需要将 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0) 拆解为我们会算的东西。首先,使用条件概率,联合概率为 q ( x t − 1 , x t , x 0 ) q(x_{t-1}, x_t, x_0) q(xt−1,xt,x0) 表示 x 0 , x t − 1 , x t x_0, x_{t-1}, x_t x0,xt−1,xt 同时出现的概率。边缘概率 q ( x t , x 0 ) q(x_t, x_0) q(xt,x0)。
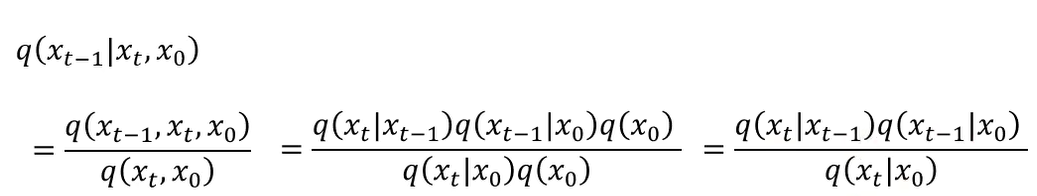
扩散模型的扩散过程是马克科夫的(当前状态仅依赖前一状态),因此 q ( x t − 1 , x t , x 0 ) = q ( x t ∣ x t − 1 ) ⋅ q ( x t − 1 ∣ x 0 ) ⋅ q ( x 0 ) q(x_{t-1}, x_t, x_0) = q(x_t | x_{t-1}) \cdot q(x_{t-1}|x_0) \cdot q(x_0) q(xt−1,xt,x0)=q(xt∣xt−1)⋅q(xt−1∣x0)⋅q(x0)。同样使用链式法则: q ( x t , x 0 ) = q ( x t ∣ x 0 ) ⋅ q ( x 0 ) q(x_t, x_0) = q(x_t | x_0) \cdot q(x_0) q(xt,x0)=q(xt∣x0)⋅q(x0)。然后约去 q ( x 0 ) q(x_0) q(x0)。最后三个部分都是高斯分布,但是两个高斯分布相乘再除以一个高斯分布到底是什么呢?

推导过程如上(跳过),最终结论还是一个高斯分布,均值和方程如下。
那么知道了 q ( x t , x 0 ) = q ( x t ∣ x 0 ) ⋅ q ( x 0 ) q(x_t, x_0) = q(x_t | x_0) \cdot q(x_0) q(xt,x0)=q(xt∣x0)⋅q(x0),那么 KL 散度怎么计算呢?
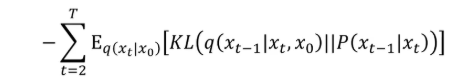
这两个分布都是高斯分布,它们的 KL 散度是有公式解的,如下:

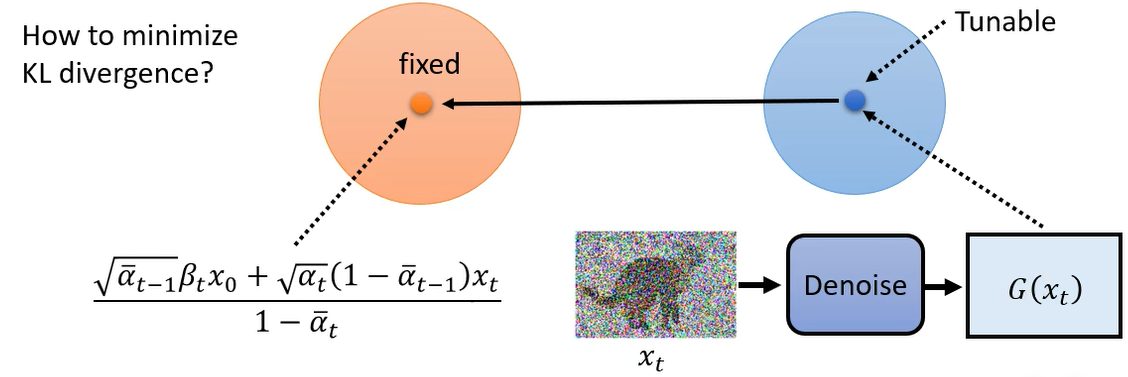
但是可以用更简单的方法来计算 KL 散度,或者说并不需要实际求出 KL 散度的值,因为我们的目标是最小化 KL 散度。那么怎么最小化呢?先看 q ( x t , x 0 ) = q ( x t ∣ x 0 ) ⋅ q ( x 0 ) q(x_t, x_0) = q(x_t | x_0) \cdot q(x_0) q(xt,x0)=q(xt∣x0)⋅q(x0) 这个高斯分布,它的均值和方差是固定的,那么 P ( x t − 1 ∣ x t ) P(x_{t-1} | x_t) P(xt−1∣xt) 呢?它是由网络决定的,这里假设不考虑方差(有文献试图讨论,但是影响很小),只考虑均值,它的均值是取决于网络,如果我们想要这两个高斯分布的 KL 散度越接近越好,一个分布是固定的,另一个分布的方差也是固定的(圆的半径是固定的),那么最小化 KL 散度的方法就是让它们的均值越接近越好。也就是将右边这个高斯分布的均值想办法跟左边的均值一模一样。
那么实际的操作是,训练这个 Denoise 模型,让它们的均值越接近越好。
那么流程如下:
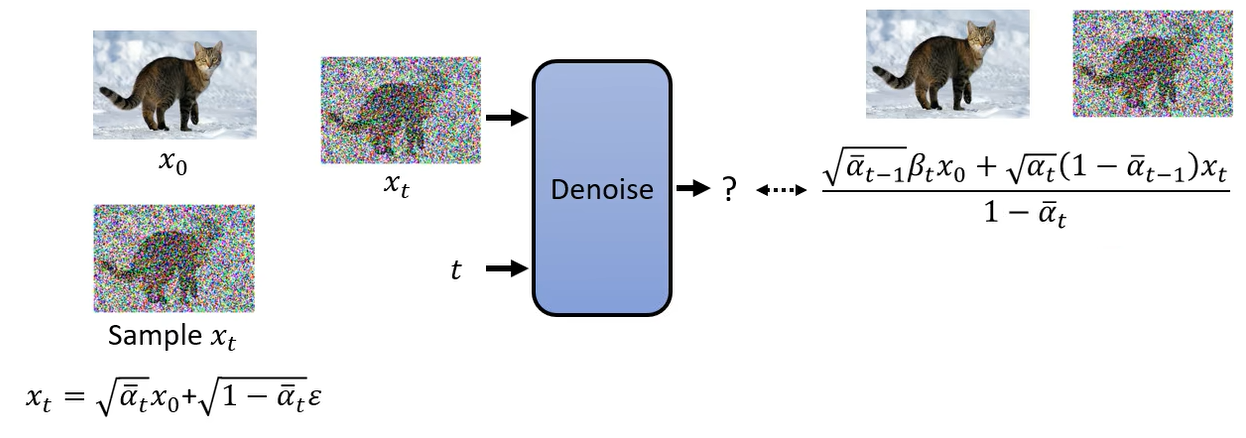
右侧的均值还可以进行化简,因为我们知道 x t 与 x 0 x_t 与 x_0 xt与x0 的关系。
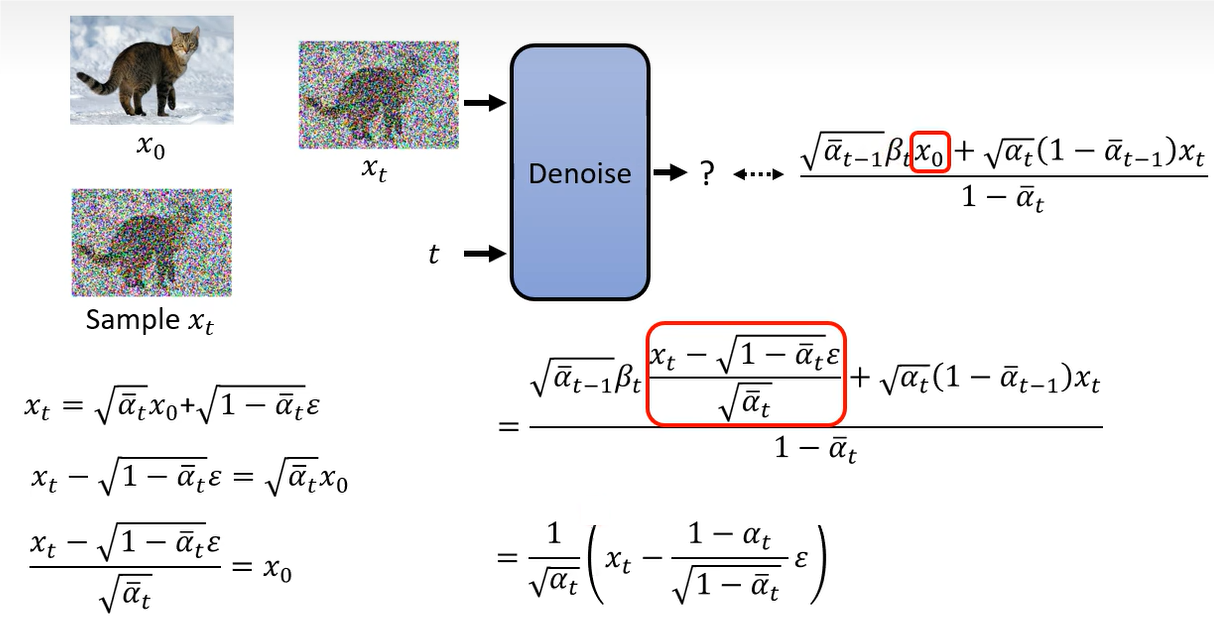
在这个均值中,其实只有 ϵ \epsilon ϵ 是需要预测的,其他都是常数,都是一开始就预定义好的。那么实际需要网络预测的部分就是 ϵ \epsilon ϵ。所以在之前的步骤中,网络的推理过程如下:

其中 β t \beta_t βt 除了预定义,也是可以学习的,但是 DDPM 证明了学习的没有预定义的效果好。给出的手工设计的建议是, β \beta β 由小到大,增加的过程就是一个线性的。
到这里还有一个问题尚未解决的是为什么不直接使用均值,还要加 σ t z \sigma_t \mathbf{z} σtz。这个在 paper 中没有找到一个答案。猜测应该是引入一定的随机性,以保持生成样本的多样性。比如我们在使用 ChatGPT 中,我们希望输入同样的问题,可以有多种答案。
