20242817-李臻-课下测试:基于商用密码的数字信封协议(AI)
课下测试:基于商用密码的数字信封协议(AI)
实验任务
- 在 Ubuntu 或 openEuler 中完成任务(推荐openEuler)理解并编译运行附件sm.zip中的代码,给出运行结果截图或运行文本内容,掌握SM2,SM3,SM4算法的使用(3分)
- 借助AI或网络,查找资料总结数字信封协议,给出基于SM2,SM3,SM4算法实现数字信封的方案(4分)
- 编程实现上面的方案,给出相关的代码或代码链接,编译与运行过程和结果截图(6分)
- 提交代码链接(github 或者 gitee)和 git log 截图(1分)
实验过程
一、代码运行
SM2
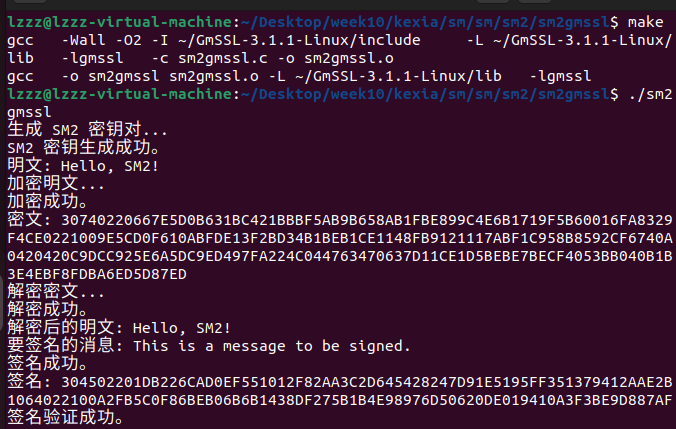
这段代码演示了使用GmSSL库实现SM2算法的基本操作。首先,它生成一对SM2密钥,并打印出来。然后,定义了一个明文字符串,使用公钥进行加密,并将加密后的密文以十六进制形式打印。接着,使用私钥对密文进行解密,并打印解密得到的明文,以验证解密过程的正确性。
此外,代码还展示了如何对一条消息进行SM2签名,并使用公钥对签名进行验证。签名过程首先初始化签名上下文,然后更新消息,最后完成签名并打印签名的十六进制形式。验证过程则是初始化验证上下文,更新消息,最后完成验证并输出验证结果。
SM3
SM4
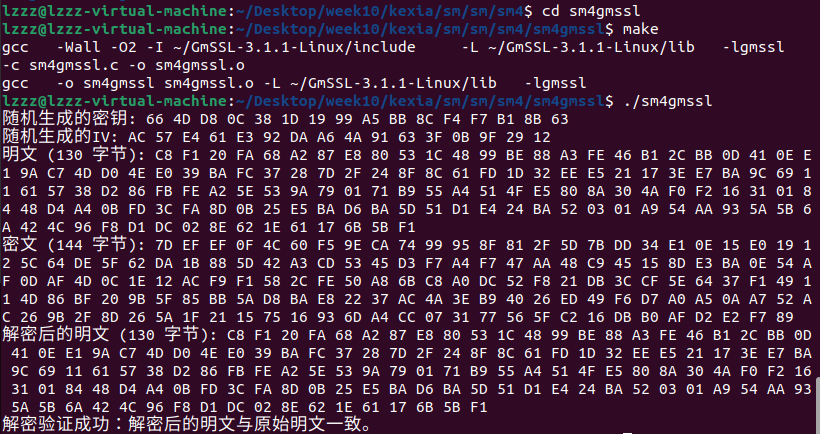
- sm4gmssl
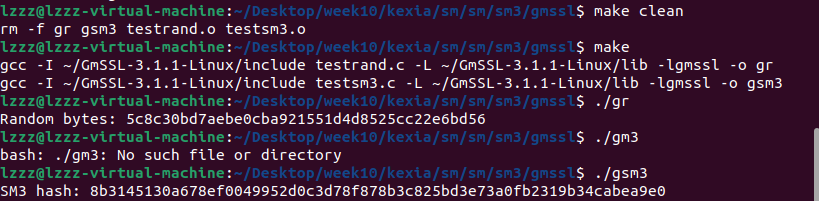
这两段代码分别演示了如何使用GmSSL库进行哈希运算和生成随机数。第一段代码使用SM3哈希算法对字符串"Hello, GmSSL SM3!"进行哈希运算,得到一个固定长度的哈希值,并以十六进制形式打印输出。SM3是中国国家标准的哈希算法,类似于SHA-256。
第二段代码演示了如何使用GmSSL的随机数生成函数rand_bytes来生成一个20字节的随机数数组,并同样以十六进制形式打印输出。这个函数用于生成加密安全的随机数,常用于密钥生成、初始化向量等安全相关的操作。
- sm4gmsslcbc
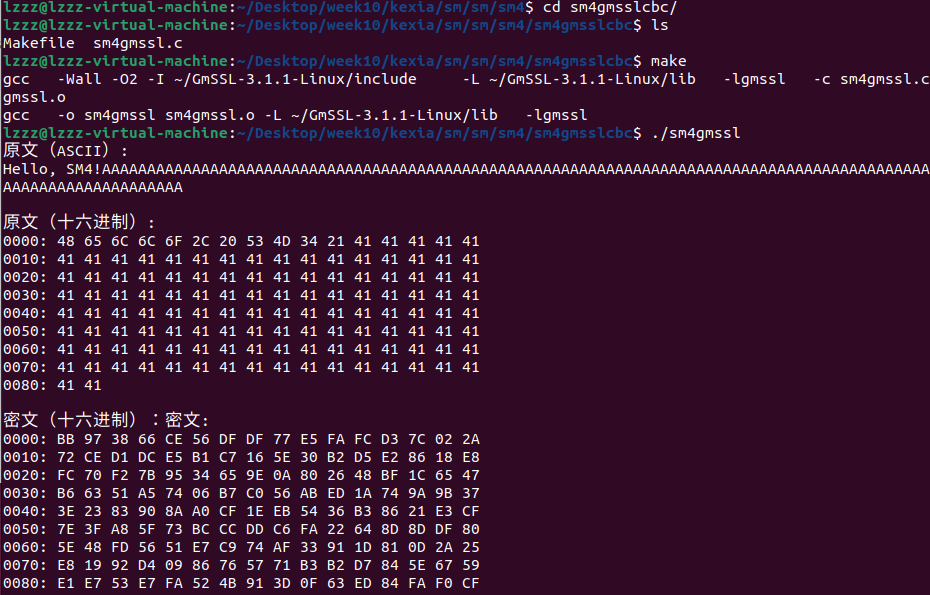
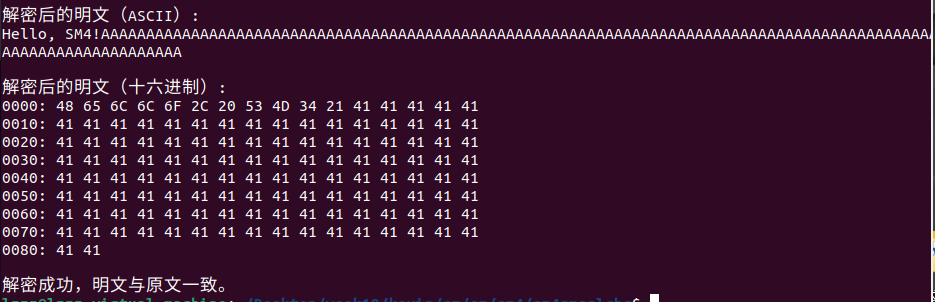
这两段代码演示了使用GmSSL库中的SM4算法进行加密和解密的过程。第一段代码生成随机的SM4密钥和初始化向量(IV),然后创建一个固定大小的明文,使用CBC模式和填充方式进行加密,之后解密并验证解密结果与原始明文是否一致。第二段代码功能类似,但增加了一个辅助函数print_hex来以十六进制形式打印数据,并在加密和解密过程中使用sm4_cbc_encrypt_init和sm4_cbc_decrypt_init等初始化函数来设置加密解密上下文。两段代码都展示了SM4算法的基本用法,包括密钥生成、加密、解密和结果验证。
二、数字信封协议
总结
数字信封协议是一种结合了对称加密和非对称加密优势的加密通信机制。在通信过程中,发送方首先使用对称加密算法对需要传输的信息进行加密,生成密文。然后,发送方随机生成一个对称加密密钥,并使用接收方的公钥对这个对称加密密钥进行加密,形成数字信封。数字信封和加密后的信息一起发送给接收方。接收方收到后,先用自己的私钥解密数字信封,得到对称加密密钥,再用这个对称加密密钥解密信息,从而获取原始明文。这种协议既利用了对称加密加密效率高的特点,又借助非对称加密解决了对称加密密钥分发困难的问题,广泛应用于需要高效安全通信的场景,如电子邮件加密和网络数据传输等。
SM2,SM3,SM4实现方案
- 在 Ubuntu 系统下,首先要确保安装了支持 SM2、SM3 和 SM4 算法的库,如 libsm 等。数字信封的实现过程主要包括以下几个步骤:
- 发送方使用 SM3 算法对明文消息进行哈希运算,生成消息摘要。这是为了保证数据的完整性,接收方可以通过对收到的明文消息进行同样的哈希运算,与发送方发送的消息摘要进行比较,来判断消息是否在传输过程中被篡改。
- 发送方随机生成一个 SM4 的对称密钥。因为 SM4 是一种对称加密算法,效率较高,适合对大量数据(即明文消息)进行加密。使用这个随机生成的对称密钥对消息摘要和明文消息一起进行 SM4 加密,得到加密后的数据。
- 发送方利用接收方的 SM2 公钥对刚才生成的 SM4 对称密钥进行加密。SM2 是一种非对称加密算法,其安全性基于椭圆曲线离散对数问题,这里使用接收方的公钥加密对称密钥,可以确保只有拥有对应私钥的接收方才能解密出对称密钥。这样,加密后的对称密钥和加密后的数据一起构成数字信封,发送给接收方。
- 接收方收到数字信封后,首先使用自己的 SM2 私钥对接收的加密后的 SM4 对称密钥进行解密,得到 SM4 对称密钥。然后利用这个对称密钥对加密后的数据进行 SM4 解密,得到消息摘要和明文消息。接着对接收到的明文消息使用 SM3 算法进行哈希运算,得到新的消息摘要,与解密得到的消息摘要进行比较,如果一致,则说明消息完整且未被篡改。
三、编程实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <gmssl/rand.h>
#include <gmssl/sm2.h>
#include <gmssl/x509.h>// 生成SM2密钥对
void generate_sm2_keypair(const char *priv_key_file, const char *pub_key_file)
{SM2_KEY sm2_key;if (!sm2_keygen(&sm2_key)) {fprintf(stderr, "Failed to generate SM2 key pair.\n");exit(1);}FILE *fp = fopen(priv_key_file, "wb");if (!fp) {perror("fopen");exit(1);}if (!sm2_key_write_private_key(fp, &sm2_key)) {fprintf(stderr, "Failed to write private key.\n");fclose(fp);exit(1);}fclose(fp);fp = fopen(pub_key_file, "wb");if (!fp) {perror("fopen");exit(1);}if (!sm2_key_write_public_key(fp, &sm2_key)) {fprintf(stderr, "Failed to write public key.\n");fclose(fp);exit(1);}fclose(fp);
}int main()
{// 生成SM2密钥对generate_sm2_keypair("sm2_private_key.pem", "sm2_public_key.pem");// 生成SM4对称密钥uint8_t sm4_key[16];if (!rand_bytes(sm4_key, sizeof(sm4_key))) {fprintf(stderr, "Failed to generate random bytes.\n");return 1;}// 使用SM2公钥加密SM4对称密钥uint8_t encrypted_sm4_key[256];size_t encrypted_sm4_key_len = sizeof(encrypted_sm4_key);SM2_KEY sm2_pub_key;FILE *fp = fopen("sm2_public_key.pem", "rb");if (!fp) {perror("fopen");return 1;}if (!sm2_key_read_public_key(fp, &sm2_pub_key)) {fprintf(stderr, "Failed to read public key.\n");fclose(fp);return 1;}fclose(fp);if (sm2_encrypt(&sm2_pub_key, sm4_key, sizeof(sm4_key), encrypted_sm4_key, &encrypted_sm4_key_len) != 1) {fprintf(stderr, "SM2 encryption failed!\n");return 1;}// 使用SM2私钥解密对称密钥uint8_t decrypted_sm4_key[16];size_t decrypted_sm4_key_len = sizeof(decrypted_sm4_key);SM2_KEY sm2_priv_key;fp = fopen("sm2_private_key.pem", "rb");if (!fp) {perror("fopen");return 1;}if (!sm2_key_read_private_key(fp, &sm2_priv_key)) {fprintf(stderr, "Failed to read private key.\n");fclose(fp);return 1;}fclose(fp);if (sm2_decrypt(&sm2_priv_key, encrypted_sm4_key, encrypted_sm4_key_len, decrypted_sm4_key, &decrypted_sm4_key_len) != 1) {fprintf(stderr, "SM2 decryption failed!\n");return 1;}// 验证解密后的对称密钥是否正确if (memcmp(sm4_key, decrypted_sm4_key, sizeof(sm4_key)) == 0) {printf("SM4 key decryption successful!\n");} else {printf("SM4 key decryption failed!\n");}return 0;
}
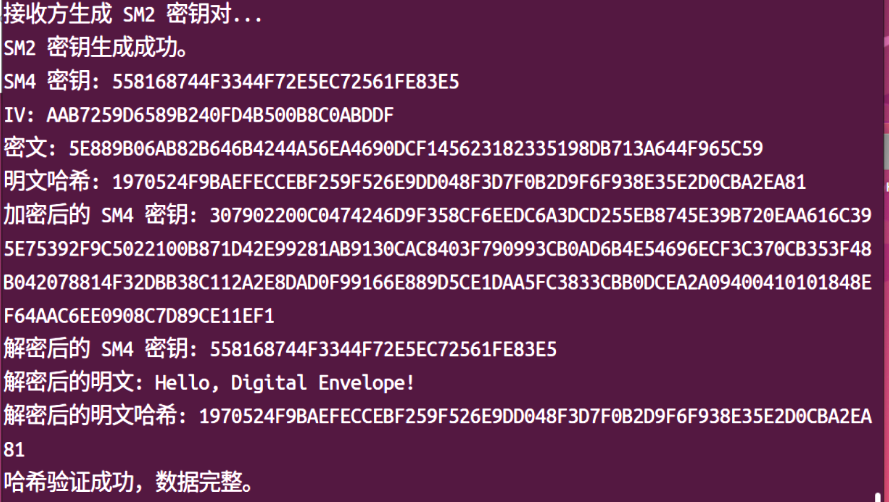
三、Giteee上传

