吴恩达机器学习笔记:多变量梯度下降
1.多维特征
之前我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为 ( x 1 , x 2 , x 3... x n ) (x1,x2,x3...xn) (x1,x2,x3...xn)
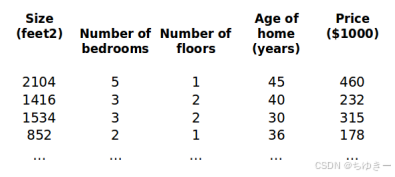
增添更多特征后,我们引入一系列新的注释:
n n n代表特征的数量
x i {x^{i }} xi代表第 i 个训练实例,是特征矩阵中的第i行,是一个向量(vector)。
x j ( i ) {x_j^{\left({i}\right)}} xj(i)代表特征矩阵中第 i行的第j个特征,也就是第i个训练实例的第 j个特征。
支持多变量的假设 ℎ 表示为: ℎθ (x) = θ0 + θ1x1 + θ2x2 +. . . +θnxn
这个公式中有个n+1参数和个n变量,为了使得公式能够简化一些,引入x0=1 则公式转化为:ℎθ (x) = θ0x0 + θ1x1 + θ2x2 +. . . +θnxn
此时模型中的参数是一个n + 1维的向量,任何一个训练实例也都是n + 1维的向量公式可以简化为:ℎθ(x) = θᵀX其中上标T代表矩阵转置。
2.多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价 函数是所有建模误差的平方和,即:
J ( θ 0 , θ 1 , … , θ n ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0, \theta_1, \dots, \theta_n) = \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 J(θ0,θ1,…,θn)=∑i=1m(hθ(x(i))−y(i))2
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为:

即:

求导得:

当n >= 1时,



我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛。
python代码示例:
def computeCost(X, y, theta):inner = np.power(((X * theta.T) - y), 2) return np.sum(inner) / (2 * len(X))
