当前位置：首页 > web >正文

【算法学习】递归、搜索与回溯算法（一）

web 2025/5/6 6:16:49

算法学习：

https://blog.csdn.net/2301_80220607/category_12922080.html?spm=1001.2014.3001.5482

前言：

这个专题与前面的相比是比较有难度的，但是在平时刷题时出现的概率还是非常高的，下面还是按照之前的逻辑来理清一下这几道题

1. 递归

1.1 汉诺塔问题

1.2 Pow(w,n)

2. 二叉树中的深搜

2.1 计算布尔二叉树的值

3. 回溯

3.1 全排列

3.2 子集

4. 总结

1. 递归

1.1 汉诺塔问题

面试题 08.06. 汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1：

 输入：A = [2, 1, 0], B = [], C = []
 输出：C = [2, 1, 0]

示例 2：

 输入：A = [1, 0], B = [], C = []
 输出：C = [1, 0]

提示：

A 中盘子的数目不大于 14 个。

算法原理：

1.首先，何为汉诺塔问题?
简单来讲，汉诺塔问题是这样的!
给定三根柱子，记为 A,B,℃ ，其中 A 柱子上有几个盘子，从上到下编号为0到n-1，目上面的盘子一定比下面的盘子小。问:将 A 柱上的盘子经由 B 柱移动到 ℃ 柱最少需要多少次?

移动时应注意:① 一次只能移动一个盘子
②大的盘子不能压在小盘子上

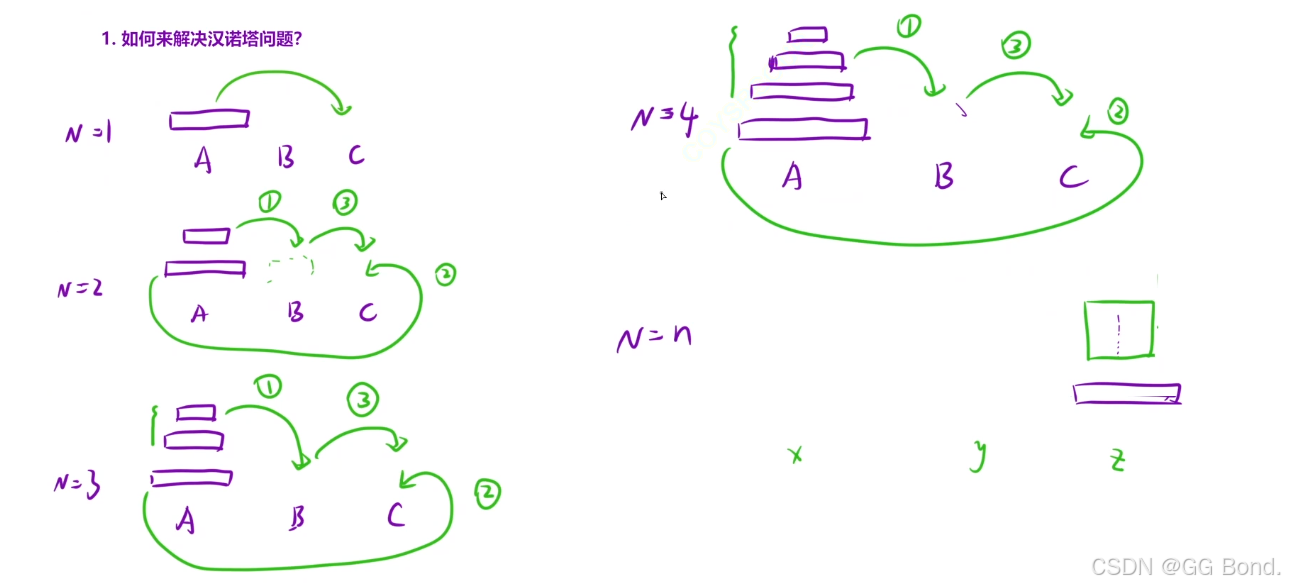
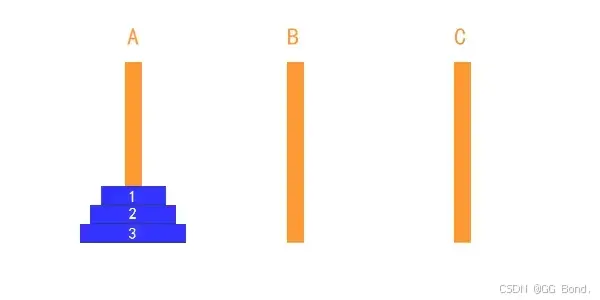
解释:

看上面的例子，当有一个盘子时直接将A柱子上的放入C上即可，当有两个盘子时，就需要借助B柱才能完成，当有三个盘子时，我们发现我们需要三步走才能完成，首先先借助C柱将A柱上3个盘子移到B柱上，然后再把A柱上剩余的那个最大的盘子移到C柱上，此时A柱上就空了，然后我们再借助A柱把B柱上的盘子移到C柱子上;
再往后，不管有多少个盘子，都是这三步这样的思路，无非就是处理次数的不同，这样来讲的话其实汉诺塔问题就符合我们上面所说的递归的条件

代码实现：

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {//目标：将A柱上所有盘子按顺序放入C柱上dfs(A,B,C,A.size());}void dfs(vector<int>& A,vector<int>& B,vector<int>& C,int n){if(n==1){C.push_back(A.back());A.pop_back();return;}//第一步，借助C柱将A柱上N-1个盘子放在B柱上dfs(A,C,B,n-1);//第二步，将A柱上剩余的那个最大盘先放到C柱上C.push_back(A.back());A.pop_back();//第三步，借助A柱将B柱上N-1个盘子全放到C柱上dfs(B,A,C,n-1);}
};

我们可以观察到我们的代码简单的有点不可思议，要相信函数递归解决重复问题的能力，只要符合子问题与父问题一致的条件，递归可以自动重复函数体中的内容，直到解决问题

1.2 Pow(w,n)

50. Pow(x, n)

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示:

-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一个整数
要么 x 不为零，要么 n > 0 。
-104 <= xn <= 104

算法原理：

解释:

看上面的这个示例，我们要求一个数的n次幂，按照一般的循环方式在这道题是会超时的，所以我们采取的是有点类似把幂二分的方法，比如3的16次方实际上就是两个3的8次方相乘，具体流程如上图所示，这种方法叫做快速幂

上边的思路我们观察一下其实就可以发现我们是可以用递归来解决这道问题的，因为每一步我们要解决的都是相同的子问题，下面我们直接看一下我们的解题代码，代码中有几个需要注意的细节点

代码实现：

class Solution {
public:double myPow(double x, int n) {return n<0?1.0/pow(x,-(long long)n):pow(x,n);}double pow(double x,long long n){if(n==0) return 1.0;double tmp=pow(x,n/2);return n%2==0?tmp*tmp:tmp*tmp*x;}
};

2. 二叉树中的深搜

2.1 计算布尔二叉树的值

2331. 计算布尔二叉树的值

给你一棵 完整二叉树 的根，这棵树有以下特征：

叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。
非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。

计算一个节点的值方式如下：

如果节点是个叶子节点，那么节点的值为它本身，即 True 或者 False 。
否则，计算两个孩子的节点值，然后将该节点的运算符对两个孩子值进行运算。

返回根节点 root 的布尔运算值。

完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。

叶子节点 是没有孩子的节点。

示例 1：

输入：root = [2,1,3,null,null,0,1]
输出：true
解释：上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ，所以我们返回 true 。

示例 2：

输入：root = [0]
输出：false
解释：根节点是叶子节点，且值为 false，所以我们返回 false 。

提示：

树中节点数目在 [1, 1000] 之间。
0 <= Node.val <= 3
每个节点的孩子数为 0 或 2 。
叶子节点的值为 0 或 1 。
非叶子节点的值为 2 或 3 。

算法原理：

我们先来看一下示例一：

我们通过这个示例来看一下这道题想让我们做什么：

首先我们通过图就能看到叶子节点上的值是布尔值，非叶子节点上的是二进制运算符，我们要做的就是从下往上把叶子节点上的值进行计算，直到计算到根节点为值，每一个非叶子节点计算后，它所保存的值就变为计算结果，可以理解成计算之后它变为了新的叶子节点

代码实现：

class Solution {
public:bool evaluateTree(TreeNode* root) {return dfs(root);}bool dfs(TreeNode* root){if(root->val==0||root->val==1) return root->val;bool left=dfs(root->left);bool right=dfs(root->right);return root->val==2?left|right:left&right;}
};

其实要想学好递归有很重要的一步，就是要相信，相信计算机能够帮助我们完成所有的其它步骤，我们要解决的只是我们这层的问题，所以看这段代码，我们要判断当前节点的运算情况，我们需要得到的是左子树和右子树的计算结果，然后我们这一层要做的就是把左右子树的计算结果运算一下就行

3. 回溯

3.1 全排列

LCR 083. 全排列

给定一个不含重复数字的整数数组 nums ，返回其 所有可能的全排列 。可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

这题我们结合代码来看吧

代码实现：

class Solution {vector<vector<int>> ret;vector<int> prev;bool check[7];
public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(prev.size()==nums.size()){ret.push_back(prev);return;}for(int i=0;i<nums.size();i++){if(check[i]==false){prev.push_back(nums[i]);check[i]=true;dfs(nums);prev.pop_back();check[i]=false;}}}
};

先来看一下决策树：

然后来看一下上面的代码都有什么作用：

解释:
1.全局变量:
首先我们先看一下我们全局变量的定义，对于回溯类的题，我们一般都需要定义全局变量，方便我们解题，因为回溯类的题型往往是需要我们记住的路径的，从而让我们能够返回上一步，所以我们定义了一个path，还定义了一个返回值ret，最后往往还需要一个布尔类型的数组check，在路径不能重复的题上，比如本题，一个路径上同一个元素只能出现一个，所以我们就需要把有重复元素的路径剪掉(剪枝)，借助check数组，我们就可以把使用过的元素进行标记，从而从另一方面实现剪枝的效果

2.dfs函数:
dfs函数体中我们只需要确保我们这一步完成工作就行

3.2 子集

LCR 079. 子集

给定一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

本题与上一题都属于回溯算法的应用

解释:

在这里我们dfs函数的处理中，我们只需要考虑两种情况，那就是当一个元素到来时，我们是选还是不选

代码实现：

class Solution {vector<vector<int>> ret;vector<int> path;
public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos==nums.size()){ret.push_back(path);return;}//因为我们要找的是数组的子集，所以对于数组中的元素，我们可以选，也可以不选，//最后可以拼接成一个含有若干元素的子集//选path.push_back(nums[pos]);dfs(nums,pos+1);path.pop_back();   //回溯//不选dfs(nums,pos+1);}
};