栈与队列 Part 2

栈的顺序存储结构及实现

栈的顺序存储结构

既然栈是线性表的特例，那么栈的顺序存储其实也是线性表顺序存储的简化，我们简称为顺序栈。线性表是用数组来实现的，想想看，对于栈这种只能一头插入删除的线性表来说，用数组哪一端来作为栈顶和栈底比较好？

对，没错，下标为0的一端作为栈底比较好，因为首元素都存在栈底，变化最小，所以让它作栈底。

我们定义一个top变量来指示栈顶元素在数组中的位置，这top就如同中学物理学过的游标卡尺的游标，如图所示，它可以来回移动，意味着栈顶的top可以变大变小，但无论如何游标不能超出尺的长度。同理，若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判定条件定为top等于－1。

来看栈的结构定义

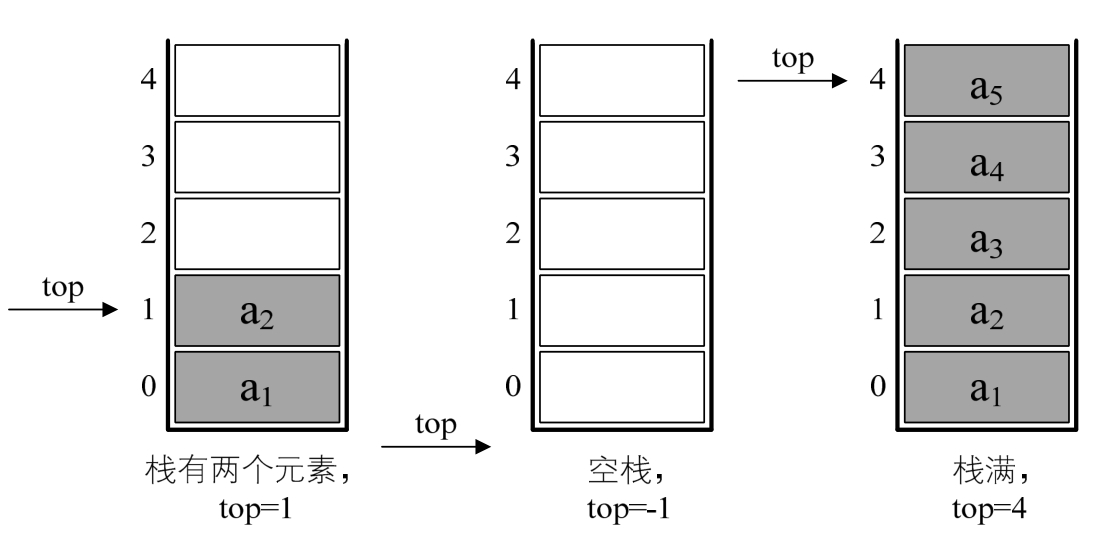
    typedef int SElemType; /* SElemType类型根据实际情况而定，这里假设为int */typedef struct{SElemType data[MAXSIZE];int top;          /* 用于栈顶指针 */}SqStack;

若现在有一个栈，StackSize是5，则栈普通情况、空栈和栈满的情况示意图如图所示。

栈的顺序存储结构—进栈操作

对于栈的插入，即进栈操作，其实就是做了如图所示的处理。

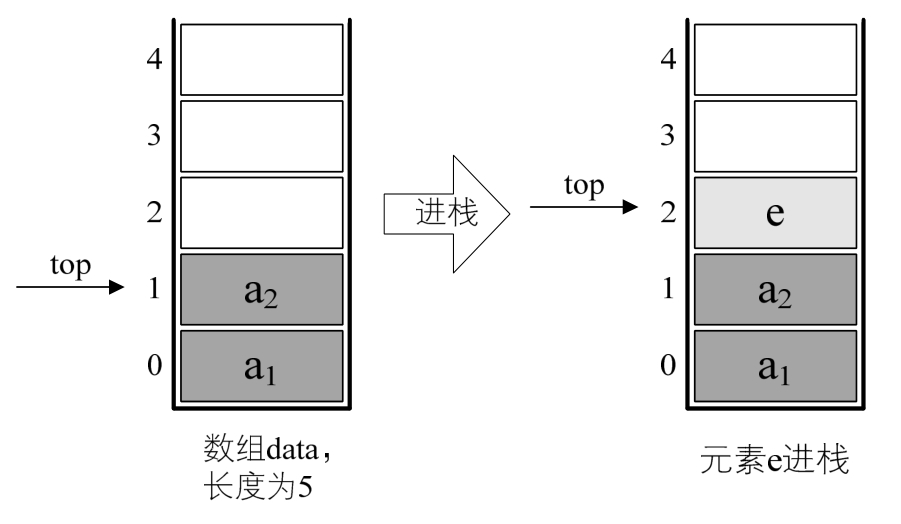
因此对于进栈操作push，其代码如下：

    /* 插入元素e为新的栈顶元素 */Status Push（SqStack *S, SElemType e）{if（S->top == MAXSIZE －1）  /* 栈满 */{return ERROR;}S->top++;                    /* 栈顶指针增加一 */S->data[S->top]=e;           /* 将新插入元素赋值给栈顶空间 */return OK;}

栈的顺序存储结构—出栈操作

出栈操作pop，代码如下：

    /* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */Status Pop（SqStack *S, SElemType *e）{if（S->top==－1）return ERROR;*e=S->data[S->top];          /* 将要删除的栈顶元素赋值给e */S->top－－;                  /* 栈顶指针减一 */return OK;}

两者没有涉及到任何循环语句，因此时间复杂度均是O(1)。

两栈共享空间

其实栈的顺序存储还是很方便的，因为它只准栈顶进出元素，所以不存在线性表插入和删除时需要移动元素的问题。不过它有一个很大的缺陷，就是必须事先确定数组存储空间大小，万一不够用了，就需要编程手段来扩展数组的容量，非常麻烦。对于一个栈，我们也只能尽量考虑周全，设计出合适大小的数组来处理，但对于两个相同类型的栈，我们却可以做到最大限度地利用其事先开辟的存储空间来进行操作。

打个比方，两个大学室友毕业同时到北京工作，开始时，他们觉得住了这么多年学校的集体宿舍，现在工作了一定要有自己的私密空间。于是他们都希望租房时能找到独住的一居室，可找来找去却发现，最便宜的一居室也要每月1500元，地段还不好，实在是承受不起，最终他俩还是合租了一套两居室，一共2000元，各出一半，还不错。

对于两个一居室，都有独立的卫生间和厨房，是私密了，但大部分空间的利用率却不高。而两居室，两个人各有卧室，还共享了客厅、厨房和卫生间，房间的利用率就显著提高，而且租房成本也大大下降了。

同样的道理，如果我们有两个相同类型的栈，我们为它们各自开辟了数组空间，极有可能是第一个栈已经满了，再进栈就溢出了，而另一个栈还有很多存储空间空闲。这又何必呢？我们完全可以用一个数组来存储两个栈，只不过需要点小技巧。

我们的做法如图所示，数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为0处，另一个栈为栈的末端，即下标为数组长度n－1处。这样，两个栈如果增加元素，就是两端点向中间延伸。

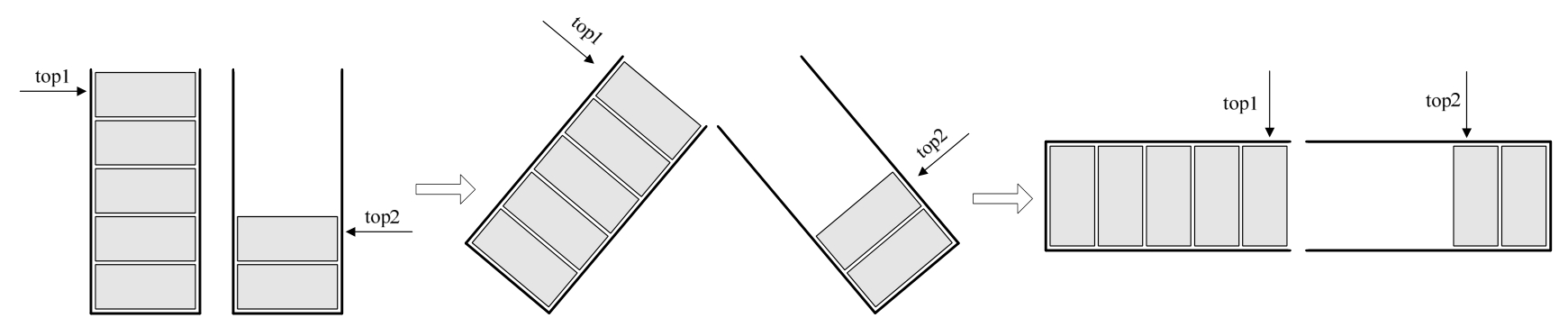
其实关键思路是：它们是在数组的两端，向中间靠拢。top1和top2是栈1和栈2的栈顶指针，可以想象，只要它们俩不见面，两个栈就可以一直使用。

从这里也就可以分析出来，栈1为空时，就是top1等于－1时；而当top2等于n时，即是栈2为空时，那什么时候栈满呢？

想想极端的情况，若栈2是空栈，栈1的top1等于n－1时，就是栈1满了。反之，当栈1为空栈时，top2等于0时，为栈2满。但更多的情况，其实就是我刚才说的，两个栈见面之时，也就是两个指针之间相差1时，即top1+1==top2为栈满。

两栈共享空间的结构的代码如下：

    /* 两栈共享空间结构 */typedef struct{SElemType data[MAXSIZE];int top1; /* 栈1栈顶指针 */int top2; /* 栈2栈顶指针 */}SqDoubleStack;

对于两栈共享空间的push方法，我们除了要插入元素值参数外，还需要有一个判断是栈1还是栈2的栈号参数stackNumber。插入元素的代码如下：

    /* 插入元素e为新的栈顶元素 */Status Push（SqDoubleStack *S, SElemType e, int stackNumber）{if （S->top1+1==S->top2）/* 栈已满，不能再push新元素了 */return ERROR;if （stackNumber==1）   /* 栈1有元素进栈 */S->data[++S->top1]=e;/* 若栈1则先top1+1后给数组元素赋值 */else if （stackNumber==2）/* 栈2有元素进栈 */S->data[－－S->top2]=e;/* 若栈2则先top2－1后给数组元素赋值 */return OK;}

因为在开始已经判断了是否有栈满的情况，所以后面的top1+1或top2－1是不担心溢出问题的。

对于两栈共享空间的pop方法，参数就只是判断栈1栈2的参数stackNumber，代码如下：

事实上，使用这样的数据结构，通常都是当两个栈的空间需求有相反关系时，也就是一个栈增长时另一个栈在缩短的情况。就像买卖股票一样，你买入时，一定是有一个你不知道的人在做卖出操作。有人赚钱，就一定是有人赔钱。这样使用两栈共享空间存储方法才有比较大的意义。否则两个栈都在不停地增长，那很快就会因栈满而溢出了。

当然，这只是针对两个具有相同数据类型的栈的一个设计上的技巧，如果是不相同数据类型的栈，这种办法不但不能更好地处理问题，反而会使问题变得更复杂，大家要注意这个前提。

栈的链式存储结构及实现

栈的链式存储结构

讲完了栈的顺序存储结构，我们现在来看看栈的链式存储结构，简称为链栈。

想想看，栈只是栈顶来做插入和删除操作，栈顶放在链表的头部还是尾部呢？由于单链表有头指针，而栈顶指针也是必须的，那干吗不让它俩合二为一呢，所以比较好的办法是把栈顶放在单链表的头部（如图所示）​。另外，都已经有了栈顶在头部了，单链表中比较常用的头结点也就失去了意义，通常对于链栈来说，是不需要头结点的。

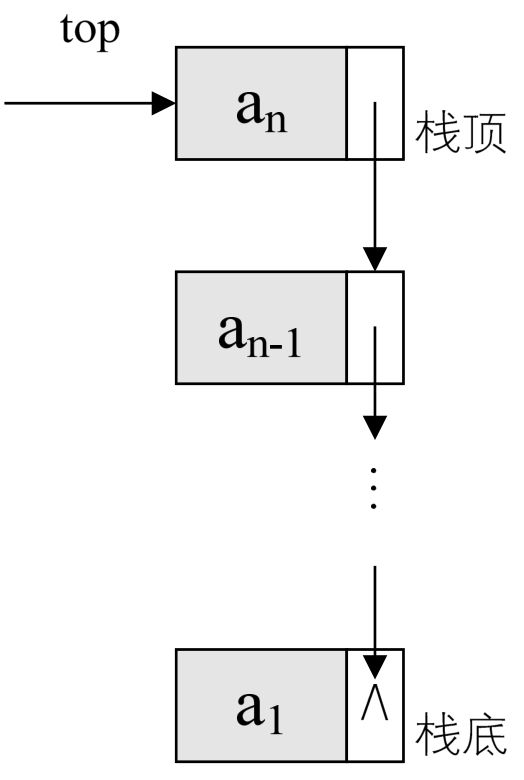
对于链栈来说，基本不存在栈满的情况，除非内存已经没有可以使用的空间，如果真的发生，那此时的计算机操作系统已经面临死机崩溃的情况，而不是这个链栈是否溢出的问题。

但对于空栈来说，链表原定义是头指针指向空，那么链栈的空其实就是top=NULL的时候。

链栈的结构代码如下：

    typedef struct StackNode{SElemType data;struct StackNode *next;}StackNode,*LinkStackPtr;typedef struct LinkStack{LinkStackPtr top;int count;}LinkStack;

链栈的操作绝大部分都和单链表类似，只是在插入和删除上，特殊一些。

栈的链式存储结构—进栈操作

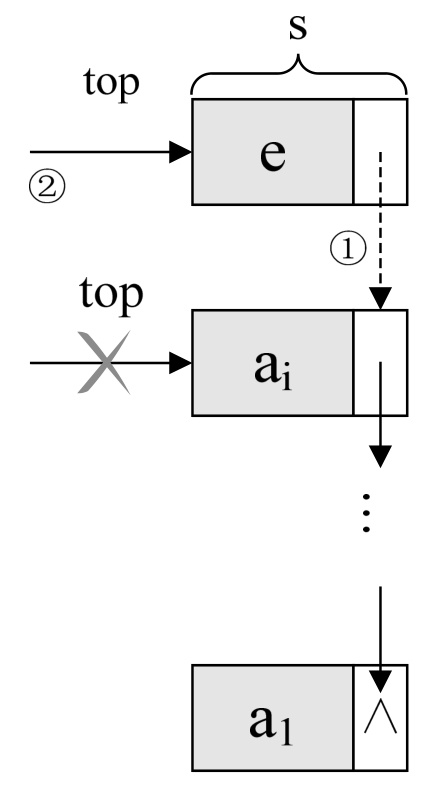
对于链栈的进栈push操作，假设元素值为e的新结点是s，top为栈顶指针，示意图如图所示代码如下。

    /* 插入元素e为新的栈顶元素 */Status Push（LinkStack *S, SElemType e）{LinkStackPtr s=（LinkStackPtr）malloc（sizeof（StackNode））;s->data=e;s->next=S->top;/* 把当前的栈顶元素赋值给新结点的直接后继，如图中① */S->top=s;      /* 将新的结点s赋值给栈顶指针，如图中② */S->count++;return OK;}

栈的链式存储结构—出栈操作

至于链栈的出栈pop操作，也是很简单的三句操作。假设变量p用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放p即可，如图所示。

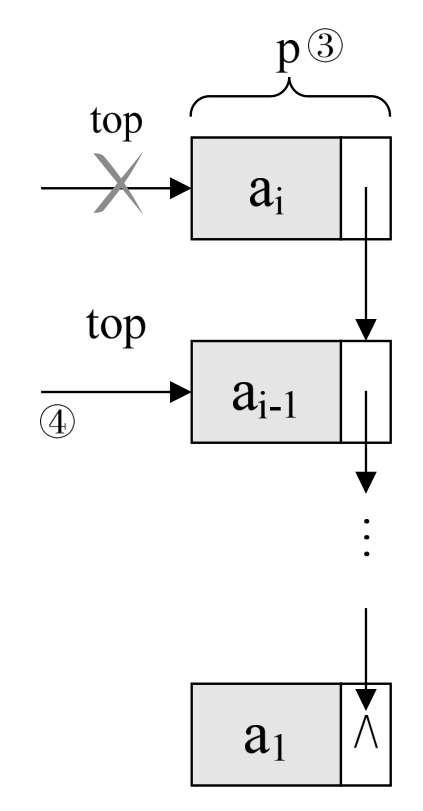
    /* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */Status Pop（LinkStack *S,SElemType *e）{LinkStackPtr p;if（StackEmpty（*S））return ERROR;*e=S->top->data;p=S->top;            /* 将栈顶结点赋值给p，如图③ */S->top=S->top->next; /* 使得栈顶指针下移一位，指向后一结点，如图④*/free（p）;           /* 释放结点p */S->count--;return OK;}

链栈的进栈push和出栈pop操作都很简单，没有任何循环操作，时间复杂度均为O(1)。

对比一下顺序栈与链栈，它们在时间复杂度上是一样的，均为O(1)。对于空间性能，顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的优势是存取时定位很方便，而链栈则要求每个元素都有指针域，这同时也增加了一些内存开销，但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样，如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序栈会更好一些。