小孔成像原理
一、总结与关键点
-
核心思想:单目成像是一个从 3D 到 2D 的投影过程,这个过程是不可逆的。它丢失了深度信息 ZcZ_cZc,这就是为什么从单张图片无法直接得到物体的真实深度(尺寸、远近)。
-
坐标系和符号定义
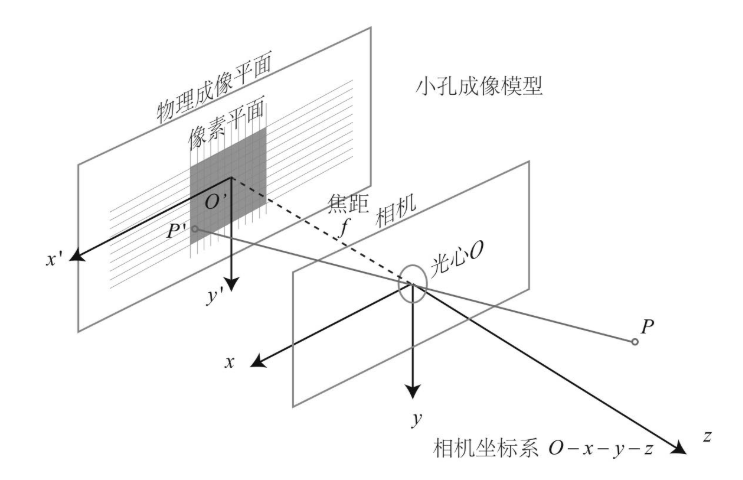
| 坐标系 | 原点 O | X轴 | Y轴 | Z轴 | 坐标符号 |
|---|---|---|---|---|---|
| 世界坐标系 | 自定义 | 自定义 | 自定义 | 自定义 | (Xw,Yw,Zw)(X_w, Y_w, Z_w)(Xw,Yw,Zw) |
| 相机坐标系 | 光心 | 与成像平面的一条边平行 | 与成像平面的一条边平行 | 与光轴重合,指向相机正前方 | (Xc,Yc,Zc)(X_c, Y_c, Z_c)(Xc,Yc,Zc) |
| 成像坐标系 | 光轴 Z_c 与成像平面的交点,称为主点 | 水平向右 | 与X轴垂直,水平向下 | 无 | (x,y)(x, y)(x,y) |
| 像素坐标系 | 通常位于图像的左上角 | 水平向右 | 与X轴垂直,水平向下 | 无 | (u,v)(u, v)(u,v) |
-
关键矩阵:
-
内参矩阵 K\mathbf{K}K:相机固有属性,(fx,fy)(f_x, f_y)(fx,fy) 是焦距,(u0,v0)(u_0, v_0)(u0,v0) 是主点。
-
外参矩阵 [R∣t][\mathbf{R} | \mathbf{t}][R∣t]:相机在世界中的位姿。
-
投影矩阵 P\mathbf{P}P:P=K[R∣t]\mathbf{P} = \mathbf{K} [\mathbf{R} | \mathbf{t}]P=K[R∣t],是整个成像过程的数学概括。
现在,我们将外参变换和内参投影结合起来,得到从世界坐标到像素坐标的完整映射关系。
Zc[uv1]=[fx0u00fyv0001]⏟内参矩阵 K[Rt0T1]⏟外参矩阵T⏟投影矩阵P[XwYwZw1]Z_c \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \underbrace{\underbrace{ \begin{bmatrix} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix} }_{\text{内参矩阵 } \mathbf{K}} \underbrace{ \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} }_{\text{外参矩阵}\mathbf{T}}}_{\text{投影矩阵}\mathbf{P}} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}Zcuv1=投影矩阵P内参矩阵 Kfx000fy0u0v01外参矩阵T[R0Tt1]XwYwZw1
通常,我们将内参矩阵 K\mathbf{K}K 和外参矩阵 [R∣t][\mathbf{R} | \mathbf{t}][R∣t] 合并为一个 3x4 的投影矩阵 P\mathbf{P}P:
P=K[R∣t]\mathbf{P} = \mathbf{K} [\mathbf{R} | \mathbf{t}]P=K[R∣t]
最终的成像模型可以简写为:
Zc⋅p=P⋅PwZ_c \cdot \mathbf{p} = \mathbf{P} \cdot \mathbf{P_w}Zc⋅p=P⋅Pw
其中 p=[u,v,1]T\mathbf{p} = [u, v, 1]^Tp=[u,v,1]T 是像素齐次坐标,Pw=[Xw,Yw,Zw,1]T\mathbf{P_w} = [X_w, Y_w, Z_w, 1]^TPw=[Xw,Yw,Zw,1]T 是世界齐次坐标。
-
二、过程推导
世界坐标系➡相机坐标系
相机坐标系和世界坐标系之间存在一个刚体变换(旋转 + 平移)。
-
两者的转换关系为:
Pc=R⋅Pw+tP_c = \mathbf{R} \cdot P_w + \mathbf{t}Pc=R⋅Pw+t
其中 R\mathbf{R}R 是一个 3x3 的旋转矩阵,t\mathbf{t}t 是一个 3x1 的平移向量。 -
写成齐次坐标形式:
[XcYcZc1]=[Rt0T1][XwYwZw1]\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}XcYcZc1=[R0Tt1]XwYwZw1我们将矩阵 [Rt0T1]\begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix}[R0Tt1] 称为相机外参矩阵。它描述了相机在世界坐标系中的位姿(位置和姿态)。
相机坐标系➡物理坐标系
-
模型设定:
- 在一个暗箱的前壁开一个无限小的孔 OOO(称为光心)。
- 暗箱的后壁是成像平面。
- 现实世界中的点 Pc(X,Y,Z)P_c (X, Y, Z)Pc(X,Y,Z)会发出一束光线。
-
成像过程:
- 这束光线中只有一条能穿过小孔 OOO,并打在成像平面的点 p(x,y)p (x, y)p(x,y)上。
- 根据相似三角形原理,我们可以立即建立关系。
-
相似三角形推导:
我们从 Y-Z 平面看(X轴同理):- 三角形 PAO和 三角形 PBO 是相似三角形。
- 因此,有比例关系:
Zf=Yy\frac{Z}{f} = \frac{Y}{y}fZ=yY
其中f是暗箱的深度,即光心O到成像平面的距离,称为焦距。 - 注意:由于光是直线传播且小孔无限小,成的像是倒立的。为了数学上的方便,我们通常会将成像平面对称地移动到光心前方(虚拟成像平面),这样得到的像是正立的,且数学关系不变。如下图所示(想象将成像平面从虚线位置移到实线位置):
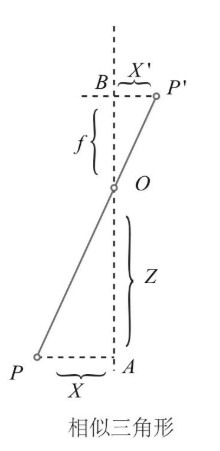
根据相似三角形,关系变为:
Zf=Yy=Xx\frac{Z}{f} = \frac{Y}{y} = \frac{X}{x}fZ=yY=xX -
得到基础公式:
由上式,我们可以立即得到:
x=f⋅XZx = f \cdot \frac{X}{Z}x=f⋅ZX
y=f⋅⋅YZy = f \cdot \cdot \frac{Y}{Z}y=f⋅⋅ZY这组公式描述了三维世界点 P 和其二维投影点 p 之间最核心的关系。
物理坐标系➡像素坐标系
我们需要将物理坐标 (x,y)(x, y)(x,y) 转换到像素坐标 (u,v)(u, v)(u,v)。
-
平移:主点 ooo在像素坐标系下通常不在 (0,0)(0, 0)(0,0),而是 (u0,v0)(u_0, v_0)(u0,v0)。所以需要平移。
u=xdx+u0u = \frac{x}{dx} + u_0u=dxx+u0
v=ydy+v0v = \frac{y}{dy} + v_0v=dyy+v0
这里 dxdxdx 和 dydydy 分别表示图像传感器上一个像素的物理宽度和高度(单位:mm/pixel)。1/dx1/dx1/dx 和 1/dy1/dy1/dy可以理解为在 x 和 y 方向上的像素密度。 -
整合:将上一步的公式 x=f⋅Xc/Zcx = f \cdot X_c / Z_cx=f⋅Xc/Zc 和 y=f⋅Yc/Zcy = f \cdot Y_c / Z_cy=f⋅Yc/Zc 代入上式:
u=fdx⋅XcZc+u0u = \frac{f}{dx} \cdot \frac{X_c}{Z_c} + u_0u=dxf⋅ZcXc+u0
v=fdy⋅YcZc+v0v = \frac{f}{dy} \cdot \frac{Y_c}{Z_c} + v_0v=dyf⋅ZcYc+v0我们令 fx=fdxf_x = \frac{f}{dx}fx=dxf, fy=fdyf_y = \frac{f}{dy}fy=dyf。fxf_xfx和 fyf_yfy 就是以像素为单位的焦距。由于制造工艺问题,fxf_xfx和 fyf_yfy可能略有不同。
