当前位置：首页 > web >正文

递归进阶之全排列、组合

web 2025/9/7 17:09:03

1.排列组合

排列：从n个元素中任取m个元素，按照一定的顺序排列起来，叫做m的全排列。

组合：从n个元素中任取m个元素为一组，m个数的组合。

注意：排列有序，组合无序。

例：从[1,2,3]三个元素中任取两个元素进行排列组合：

排列的结果：[1,2] 、[1,3]、[2,1]、[2,3]、[3,1]、[3,2]

组合的结果：[1,2]、[1,3]、[2,3]

例题：n个元素的全排列，（n互不相同，即1，2，······n）.

#include<iostream>
#include<cmath>
using namespace std;  
//n个数全排列 ：一定要知道在第几层，该数现在的状态，回溯时的状态 int n;
int a[1000];
bool flag[1000];
void dfs(int k){if(k==n+1){  //递归结束条件，当到达第n+1层，代表第n层已经填完 for(int i=1; i<=n; i++){cout<<a[i]<<" ";}cout<<endl; return;}for(int i=1; i<=n; i++){  //n个数字 if(flag[i]==0){  //当前数字没用过才可以排列 a[k]=i;   //第k层（第k个位置）填数字iflag[i]=1;  //该数已经用过，置为1dfs(k+1);    //填下一层（下一个位置）flag[i]=0;   //递归回来的时候需要重新置为0 }}}int main(){cin>>n;dfs(1);  //从第一层（第一个位置）开始排列 return 0;
}

程序运行结果如下：

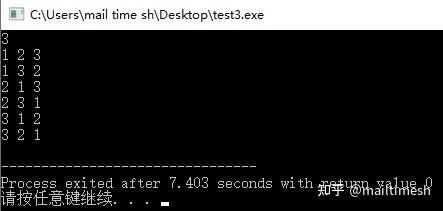
例2：n个数选m个数全排列

#include<iostream>
#include<cmath>
using namespace std;  
//n个数选m个数全排列 ：一定要知道在第几层，该数现在的状态，回溯时的状态 int n,m;
int a[1000];
bool flag[1000];
void dfs(int k){if(k==m+1){  //递归结束条件，当到达第m+1层，代表第m层已经填完 for(int i=1; i<=m; i++){cout<<a[i]<<" ";}cout<<endl; return;}for(int i=1; i<=n; i++){  //n个数字 if(flag[i]==0){  //当前数字没用过才可以排列 a[k]=i;   //第k层（第k个位置）填数字iflag[i]=1;  //该数已经用过，置为1dfs(k+1);    //填下一层（下一个位置）flag[i]=0;   //递归回来的时候需要重新置为0 }}}int main(){cin>>n>>m;dfs(1);  //从第一层（第一个位置）开始排列 return 0;
}

程序运行如下：

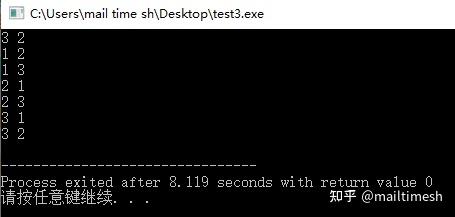
例3：n个不同的元素，任取m个数进行组合。（组合无序）

#include<iostream>
#include<cmath>
using namespace std;  
//n个数选m个数组合 ：当前位置数值比前一个数至少大1，
//a[k]代表当前位置上的值，它的范围是[a[k-1]+1,n] int n,m;
int a[1000];void dfs(int k){if(k==m+1){  //递归结束条件，当到达第m+1层，代表第m层已经填完 for(int i=1; i<=m; i++){cout<<a[i]<<" ";}cout<<endl; return;} //当前位置数值比前一个数至少大1，a[k]代表当前位置上的值，它的范围是[a[k-1]+1,n] for(int i=a[k-1]+1; i<=n; i++){  a[k]=i;   //第k层（第k个位置）填数字idfs(k+1);    //填下一层（下一个位置）}
}int main(){cin>>n>>m;dfs(1);  //从第一层（第一个位置）开始排列 return 0;
}

程序运行如下：

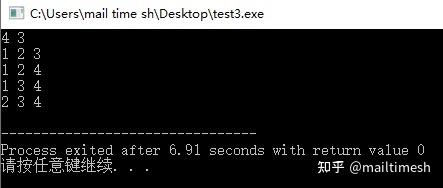
2.铺骨牌问题

有一个1*n的长方形，用1*1、1*2、1*3的骨牌铺满方格，共有几种铺法。

分析如下：

本题采用递归函数，当确定最后一块方式后，只需看前面的格子共有几种铺法即可。而最后一个格子的铺法不确定，所以要各种方案的总方案数相加才行。

即：f(n)=f(n-1)+f(n-2)+f(n-3).

程序如下：

#include<iostream>
#include<cmath>
using namespace std;  
int f(int x){if(x==1) return 1;  if(x==2) return 2;if(x==3) return 4;return f(x-1)+f(x-2)+f(x-3);  //共三种格子 //f(x)的方案数为 末尾放1*1，前面总方案为f(x-1)；//尾放1*2，前面总方案为f(x-2)； 尾放1*3，前面总方案为f(x-3)  
}
int main(){int n;cin>>n;cout<<f(n); return 0;
}