数据结构（C语言篇）：（六）单链表算法题（下）

目录

前言

一、链表的回文结构

二、相交链表

三、环形链表​编辑

四、环形链表II

总结

---

前言

        本篇博客将继续介绍单链表相关的算法题，包括了链表的回文结构、相交链表、环形链表等。现在就让我们正式开始吧！

---

一、链表的回文结构

        题目链接：链表的回文结构_牛客题霸_牛客网

        思路：创建数组（大小为900），遍历链表将节点的值依次存储在数组中，若数组为回文结构，则链表为回文结构。

        解题核心逻辑如下：

1. 将链表值复制到数组：遍历链表，将所有节点的值存储到数组中；

2. 使用双指针判断回文：从数组两端向中间遍历，比较对应位置的值是否相等；

3. 返回判断结果：如果所有对应位置都相等，则是回文；否则不是。

        完整代码如下所示：

class PalindromeList {
public:bool chkPalindrome(ListNode* A) {// 创建固定大小的数组int arr[900] = {0};  // 假设链表长度不超过900// 遍历链表，将值存储到数组中ListNode* pcur = A;int i = 0;while(pcur) {arr[i++] = pcur->val;  // 存储当前节点值，i后移pcur = pcur->next;     // 移动到下一个节点}// 使用双指针判断数组是否为回文int left = 0, right = i - 1;  // i是链表长度while(left < right) {if(arr[left] != arr[right]) {return false;  // 发现不对称，不是回文}left++;right--;}return true;  // 所有对应位置都相等，是回文}
};

        代码的执行流程示例如下：假设链表为1 → 2 → 3 → 2 → 1 → NULL

步骤1：复制到数组
遍历链表：arr[0]=1, arr[1]=2, arr[2]=3, arr[3]=2, arr[4]=1
i=5（链表长度）步骤2：双指针判断
left=0, right=4: 1==1 ✓
left=1, right=3: 2==2 ✓  
left=2, right=2: 循环结束
返回true

二、相交链表

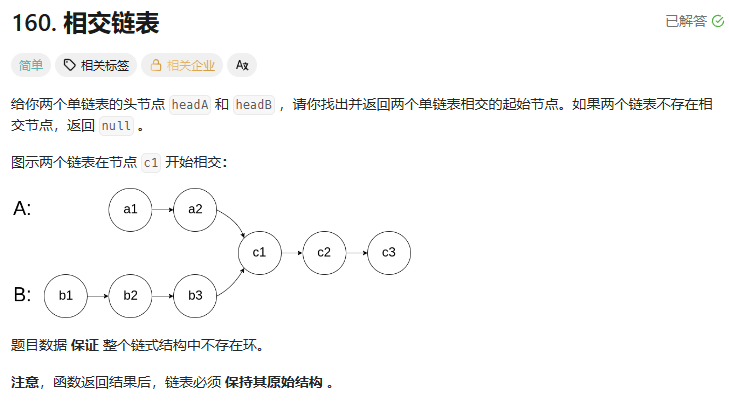
        题目链接：160. 相交链表 - 力扣（LeetCode）

        思路：求两个链表的长度，长链表先走长度差步，短链表开始同步遍历，找相同的结点。

        解题核心逻辑如下：

1. 计算链表长度：分别遍历两个链表，计算它们的长度；

2. 计算长度差：求出两个链表长度的差值；

3. 对齐起点：让较长的链表先移动长度差的步数；

4. 同时遍历：两个指针同时移动，直到找到相同节点或到达末尾。

        完整代码如下：

typedef struct ListNode ListNode;struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {// 求链表的长度ListNode* pa = headA;ListNode* pb = headB;int sizeA = 0, sizeB = 0;// 计算链表A的长度while(pa) {++sizeA;pa = pa->next;}// 计算链表B的长度while(pb) {++sizeB;pb = pb->next;}// 求长度差int gap = abs(sizeA - sizeB);  // 求绝对值// 定义长短链表ListNode* shortList = headA;ListNode* longList = headB;// 确定哪个链表更长if(sizeA > sizeB) {longList = headA;shortList = headB;}// 长链表先走gap步，对齐起点while(gap--) {longList = longList->next;}// shortList和longList现在在同一起跑线while(shortList) {  // 或者用while(longList)if(shortList == longList) {  // 找到相交节点return shortList;}shortList = shortList->next;longList = longList->next;}// 链表不相交return NULL;
}

        执行流程的示例如下：

        假设：
        链表A：1 → 2 → 3 → 4 → 5 → NULL（长度5）
        链表B：9 → 8 → 4 → 5 → NULL（长度4，从节点4开始相交）

步骤1：计算长度
sizeA = 5, sizeB = 4步骤2：计算长度差
gap = |5-4| = 1步骤3：确定长短链表
longList = headA, shortList = headB步骤4：长链表先走1步
longList从节点1移动到节点2步骤5：同时遍历
shortList=9, longList=2 → 不相等
shortList=8, longList=3 → 不相等  
shortList=4, longList=4 → 相等，返回节点4

三、环形链表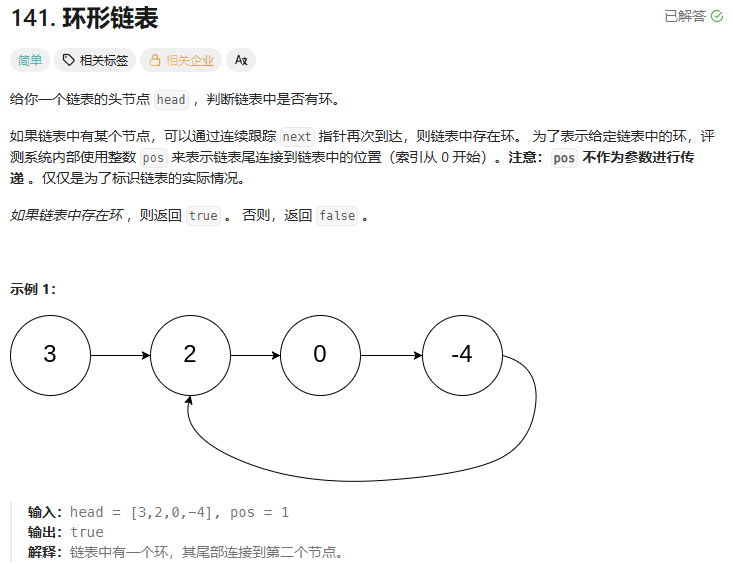

        题目链接：141. 环形链表 - 力扣（LeetCode）

        思路：采用快慢指针方法，慢指针每次走一步，快指针每次走两步，如果slow和fast指向了同一个结点，说明链表带环。

        对于这个思路，我们可以尝试证明一下：

        证明1：在环形链表中，慢指针每次走一步，快指针每次走两步，最终是否一定会相遇？

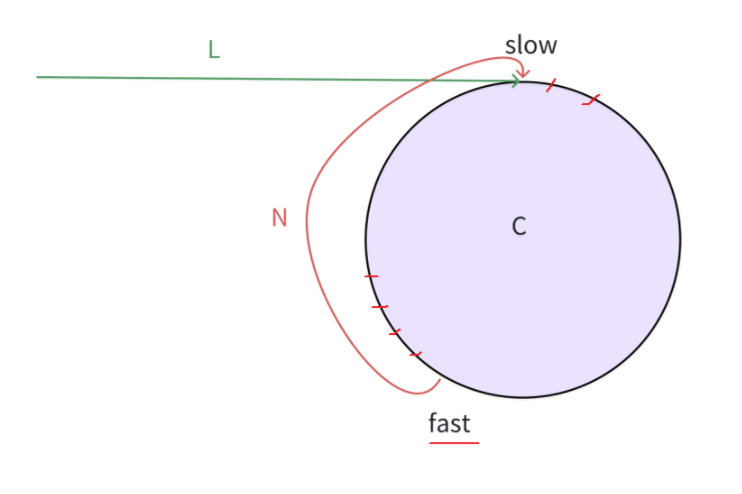
        如上图所示，假设此时slow刚入环，此时slow和fast之间的距离最大，为N。slow和fast各自移动一次之后，距离缩小2 - 1 = 1，则此时距离为N - 1，那么在移动N次之后，最后fast和slow之间的距离将缩短为0，两指针相遇。

        证明2：在环形链表中，慢指针每次走一步，快指针每次走3、4、5、……步，快慢指针在环形链表中还会相遇吗？答案是一定会相遇。

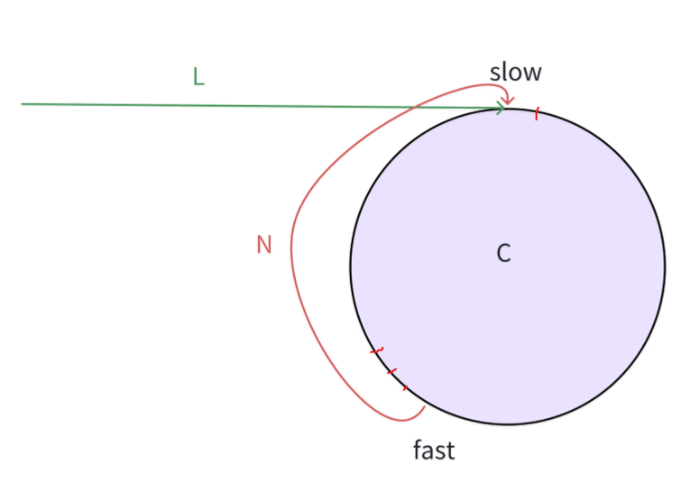
        如上图，假设此时slow刚入环，此时slow和fast之间的距离最大，为N。慢指针每次走一步，快指针每次走三步。每走一次，slow和fast之间距离就减小2，此时若N为偶数，那么最后两者距离将减小为0，相遇；若N为奇数，那么距离会缩小为-1，此时就会套圈，两者此时距离须以C-1来计算。若C-1为偶数，即C为奇数，那么一定会相遇；如果C-1为奇数，即C为偶数，则一定不会相遇。

        下面我们再来推导一下快慢指针走的路程之间的关系：

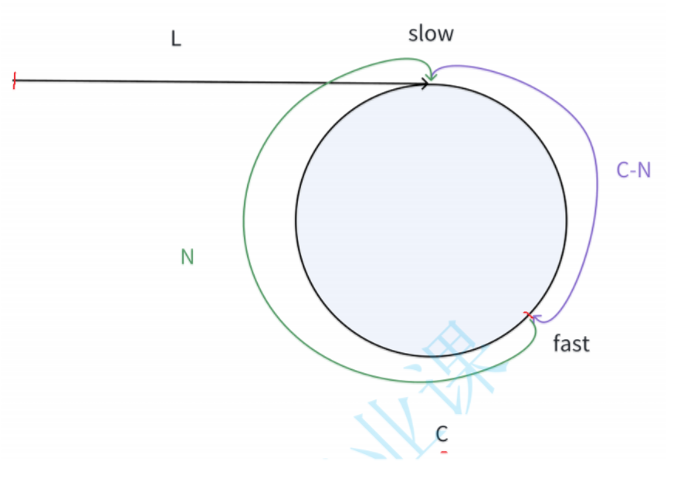
        如上图，我们假设慢指针每次走1步，快指针一次走3步，那么就有：3 * 慢指针 = 快指针。我们假设慢指针所走路程为L，则快指针所走路程为：L + C - N + nC。根据以上等式，就有：3L = L + C - N + nC，整理得到：2L = （n+1）C - N。如下：

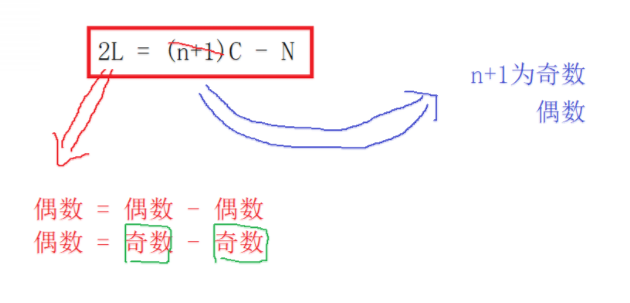
💡TIPS

        虽然我们已经证明了快指针无论走多少步都可以满足在带环链表中相遇，但是在编写代码的时候会有额外的步骤引入，涉及到快慢指针的算法题中通常习惯使用慢指针走一步快指针走两步的方式。

        因此本题我们解题的核心逻辑如下：

       1.  初始化两个指针：

        slow（慢指针）：每次移动一步；

        fast（快指针）：每次移动两步。

        2.  同时移动指针：

                慢指针每次移动1步，快指针每次移动2步；

                如果链表有环，快慢指针最终会相遇；

                如果链表无环，快指针会先到达NULL。

        3.  终止条件：

                快慢指针相遇 → 有环，返回true；

                快指针到达NULL → 无环，返回false。

        完整代码如下：

typedef struct ListNode ListNode;bool hasCycle(struct ListNode *head) {// 创建快慢指针ListNode* slow = head;  // 慢指针，每次移动1步ListNode* fast = head;  // 快指针，每次移动2步// 循环条件：快指针和快指针的下一个节点都不为NULLwhile(fast && fast->next) {slow = slow->next;        // 慢指针移动1步fast = fast->next->next;  // 快指针移动2步if(slow == fast) {        // 如果相遇return true;          // 链表有环}}// 快指针到达NULL，链表不带环return false;
}

        下面提供两个执行流程的示例：

        1.  有环链表：1 → 2 → 3 → 4 → 5 → 3（形成环）

初始：slow=1, fast=1
第1轮：slow=2, fast=3
第2轮：slow=3, fast=5  
第3轮：slow=4, fast=3
第4轮：slow=5, fast=5 → 相遇，返回true初始：slow=1, fast=1
第1轮：slow=2, fast=3
第2轮：slow=3, fast=5  
第3轮：slow=4, fast=3
第4轮：slow=5, fast=5 → 相遇，返回true

        2.  无环链表： 1→ 2 → 3 → 4 → 5 → NULL

初始：slow=1, fast=1
第1轮：slow=2, fast=3
第2轮：slow=3, fast=5
第3轮：slow=4, fast=NULL → 循环结束，返回false

四、环形链表II

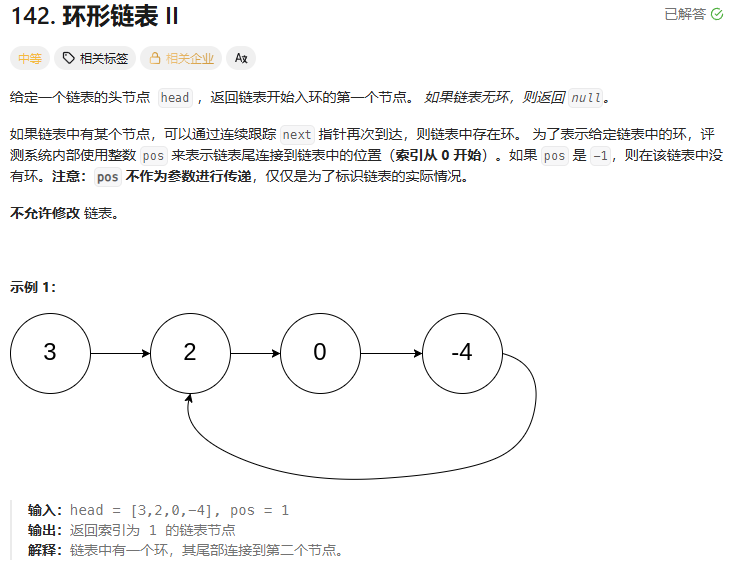
        题目链接：142. 环形链表 II - 力扣（LeetCode）

        思路：快慢指针，在环里一定会相遇。相遇点到入环结点的距离 == 头结点到入环结点的距离

💡结论

        让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。

        下面我们先来证明一下以上结论：

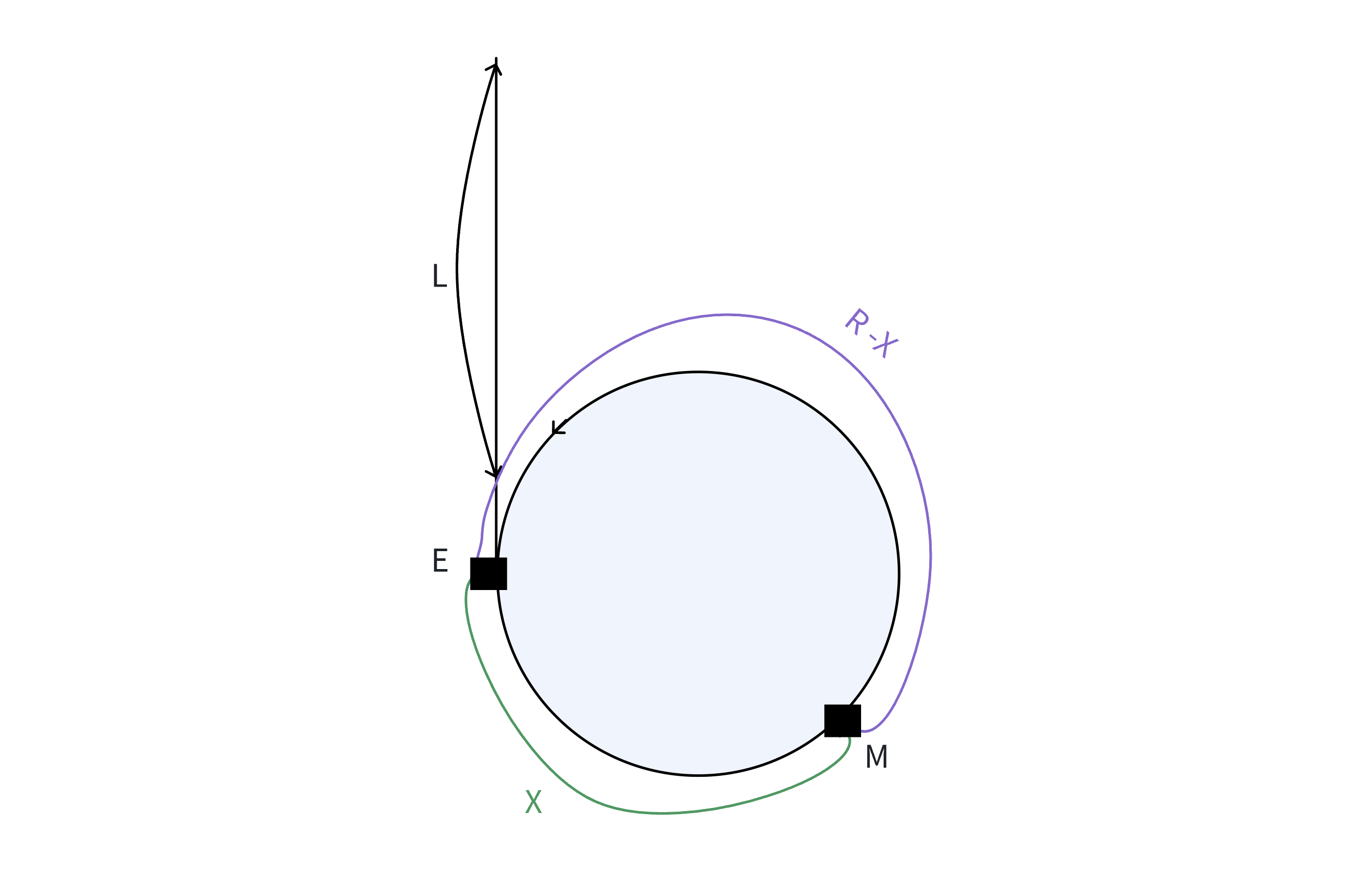
        H为链表的起始点，E为环的入口点，M与判环时候相遇点。

        假设：环的长度为R，H到E的距离为L，E到M的距离为X，则：M到E的距离为R - X。

        在判环的时候，快慢指针相遇时所走的路径长度如下：

• fast：L + X + nR
• slow：L + X 

        需要注意的是：

        1.  当慢指针进入环时，快指针可能已经在环中绕了n圈了，n至少为1。因为当快指针先进环走到M的位置，最后又会在M的位置与慢指针相遇。

        2.  慢指针进入环之后，快指针肯定会在慢指针走一圈之内追上慢指针。因为当慢指针进环之后，快慢指针之间的距离最多就是环的长度，而两个指针在移动的时候，每次它们的距离都缩减一步，因此在慢指针移动一圈之前，快指针肯定是可以追上慢指针的，而快指针的速度是慢指针的两倍，因此有如下关系：

        2 * (L + X) = L + X + nR；

        L + X = nR；

        L = nR - X；

        L = (n - 1)R + (R - X)

        （n = 1、2、3、4、……、n，n的大小取决于环的大小，环越小n越大）

        在极端情况下，我们假设n = 1，此时有：L = R - X。

        即：一个指针从链表起始位置运行，一个指针从相遇点位置绕环，每次都走一步，两个指针最终会在入口点的位置相遇。

        完整代码如下：

typedef struct ListNode ListNode;struct ListNode *detectCycle(struct ListNode *head) {// 创建快慢指针ListNode* slow = head;  // 慢指针，每次移动1步ListNode* fast = head;  // 快指针，每次移动2步// 第一阶段：判断是否有环while(fast && fast->next) {slow = slow->next;        // 慢指针移动1步fast = fast->next->next;  // 快指针移动2步if(slow == fast) {        // 如果相遇，说明有环// 第二阶段：寻找环入口// 数学原理：头节点到入口的距离 = 相遇点到入口的距离ListNode* pcur = head;while(pcur != slow) {pcur = pcur->next;  // pcur从头节点开始slow = slow->next;  // slow从相遇点开始}return pcur;  // 相遇点即为环入口}}// 快指针到达NULL，链表不带环return NULL;
}

        执行流程示例如下：1 → 2 → 3 → 4 → 5 → 3（形成环，入口在节点3）

步骤1：判断有环
slow=1, fast=1
slow=2, fast=3
slow=3, fast=5  
slow=4, fast=3
slow=5, fast=5 → 相遇在节点5

步骤2：寻找环入口
pcur=head=1, slow=5
pcur=2, slow=3
pcur=3, slow=3 → 相遇在节点3（环入口）
返回节点3

---

总结

        以上就是本期单链表算法题的全部内容啦~~~下期博客我将为大家带来双向链表的相关知识介绍，请大家多多关注、多多支持哦！