树状数组【原理+详解+例题】
文章目录
- 原理
- lowbit函数
- 构建与操作
- 构建
- 单点更新
- 前缀查询
- 扩展
- 差分转化
- 例题训练
- P3374 【模板】树状数组 1
- AC代码
- P3368 【模板】树状数组 2
- AC代码
在算法的世界里,高效处理区间查询和单点更新是常见需求。树状数组作为一种巧妙的数据结构,凭借简洁的实现、优秀的时间复杂度,成为这类问题的“得力助手”。
首先对比一下树状数组和线段树的区别:
大家可以看一下这篇对线段树的讲解:线段树:从入门到精通
| 特性 | 树状数组 | 线段树 |
|---|---|---|
| 结构 | 基于二进制分层的“简化树” | 完全二叉树结构 |
| 空间复杂度 | O(N)O(N)O(N) | O(4N)O(4N)O(4N)(通常开4倍空间) |
| 时间复杂度 | 单点更新/前缀查询均为 O(logN)O(\log N)O(logN) | 区间查询/更新均为 O(logN)O(\log N)O(logN) |
| 适用场景 | 满足结合律+可差分的操作(如求和、异或) | 更通用,支持复杂区间操作 |
| 代码实现 | 简短、常数小 | 代码较长,常数较大 |
简单说:树状数组是线段树的“优化子集”,适合前缀和/单点更新类问题,实现更轻量。
那么接下来我们详细介绍下树状数组:
原理
核心思想:分层管理
树状数组的本质是用数组模拟树形结构,通过二进制分解,让每个节点管理一段区间的信息。例如,对于长度为8的数组:
s[8]管理a[1]~a[8]s[4]管理a[1]~a[4]s[6]管理a[5]~a[6](二进制6=4+2,对应区间长度2)
这种分层,让前缀和查询和单点更新能通过“跳二进制位”快速完成。
lowbit函数
lowbit(x) 的作用是提取x的最低位1对应的数值,公式为:
int lowbit(int x) {return x & -x;
}
- 示例:
x=6(二进制110),-x是010(补码),x & -x = 2(二进制10),即最低位1对应的值是2。
lowbit 决定了树状数组的“跳跃规则”:
- 更新时:从当前节点出发,不断
x += lowbit(x),向上更新父节点。 - 查询时:从当前节点出发,不断
x -= lowbit(x),累加区间信息。
构建与操作
构建
逐层累加
树状数组的构建,本质是让每个节点
s[i]管理其“覆盖区间”的信息。
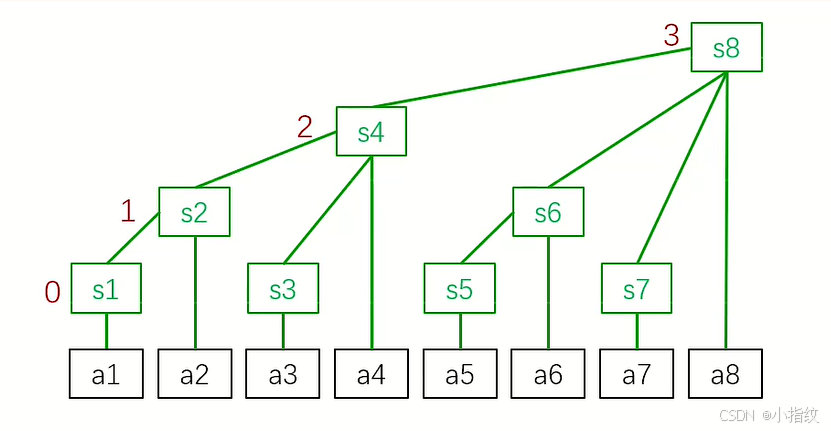
参照该图,以求和为例:
s[1]管理a[1](lowbit(1)=1,区间长度1)s[2]管理a[1]~a[2](lowbit(2)=2,区间长度2)s[3]管理a[3](lowbit(3)=1,区间长度1)s[4]管理a[1]~a[4](lowbit(4)=4,区间长度4)
构建时,每个 a[i] 会被加入到 s[i]、s[i+lowbit(i)] 等节点中,形成“分层管理”。
单点更新
向上传递变化
当修改
a[x]的值(比如增加k),需要更新所有包含a[x]的s节点:
void change(int x, int k) {while (x <= n) { s[x] += k; // 更新当前节点x += lowbit(x); // 跳到父节点}
}
前缀查询
向下累加区间
查询
a[1]~a[x]的和,需要累加所有覆盖该区间的s节点:
int query(int x) {int res = 0;while (x > 0) { res += s[x]; // 累加当前节点x -= lowbit(x); // 跳到子区间}return res;
}
扩展
区间更新与单点查询的差分技巧
树状数组默认处理单点更新+前缀查询,但通过差分思想,可扩展为区间更新+单点查询。
问题场景
操作1:将区间 [l, r] 的每个数加 k
操作2:查询某个点 x 的值
差分转化
利用差分数组的性质:
- 差分数组
d[i] = a[i] - a[i-1] - 区间
[l, r]加k→ 等价于d[l] +=k,d[r+1] -=k - 查询
a[x]→ 等价于求d[1]~d[x]的前缀和
(因为a[x] = d[1]+d[2]+...+d[x])
代码实现
// 树状数组管理差分数组d的前缀和
void change(int x, int k) {while (x <= n) {s[x] += k;x += lowbit(x);}
}// 区间 [l, r] 加 k
void range_add(int l, int r, int k) {change(l, k); // d[l] +=kchange(r+1, -k); // d[r+1] -=k
}// 查询点x的值(即a[x])
int query_point(int x) {int res = 0;while (x > 0) {res += s[x];x -= lowbit(x);}return res;
}
原理:通过差分数组,将“区间更新”转化为“两个单点更新”,再利用树状数组的前缀查询得到单点值。
例题训练
P3374 【模板】树状数组 1
题目来源
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 xxx;
-
求出某区间每一个数的和。
输入格式
第一行包含两个正整数 n,mn,mn,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 nnn 个用空格分隔的整数,其中第 iii 个数字表示数列第 iii 项的初始值。
接下来 mmm 行每行包含 333 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 xxx 个数加上 kkk; -
2 x y含义:输出区间 [x,y][x,y][x,y] 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 222 的结果。
输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 #1
14
16
说明/提示
【数据范围】
对于 30%30\%30% 的数据,1≤n≤81 \le n \le 81≤n≤8,1≤m≤101\le m \le 101≤m≤10;
对于 70%70\%70% 的数据,1≤n,m≤1041\le n,m \le 10^41≤n,m≤104;
对于 100%100\%100% 的数据,1≤n,m≤5×1051\le n,m \le 5\times 10^51≤n,m≤5×105。
数据保证对于任意时刻,aaa 的任意子区间(包括长度为 111 和 nnn 的子区间)和均在 [−231,231)[-2^{31}, 2^{31})[−231,231) 范围内。
样例说明:
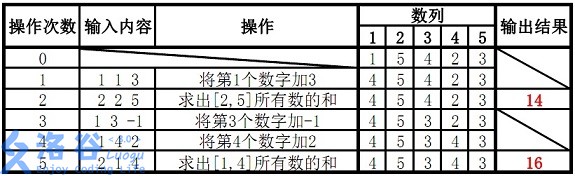
故输出结果 141414 和 161616。
该模板题要求的是单点更新和区间查询
AC代码
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
int n,m,a[N],s[N],op,x,y,k;
int lowbit(int x)
{return x&-x;
}
void update(int x,int k)//单点更新,在x位置增加k
{while(x<=n){s[x]+=k;x+=lowbit(x); }
}
int ask(int x)//前缀查询,查询1~x的和
{int ans=0;while(x>0){ans+=s[x];x-=lowbit(x);}return ans;
}
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)update(i,a[i]);while(m--){cin>>op;if(op==1)//单点更新操作 {cin>>x>>k;update(x,k);}else//区间查询操作 {cin>>x>>y;cout<<ask(y)-ask(x-1)<<endl;//区间和=前缀和[y]-前缀和[x-1] }}
}
signed main()
{IOS;int _=1;
// cin>>_;while(_--)solve();return 0;
}P3368 【模板】树状数组 2
题目来源
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 xxx;
-
求出某一个数的值。
输入格式
第一行包含两个整数 NNN、MMM,分别表示该数列数字的个数和操作的总个数。
第二行包含 NNN 个用空格分隔的整数,其中第 iii 个数字表示数列第 $i $ 项的初始值。
接下来 MMM 行每行包含 222 或 444 个整数,表示一个操作,具体如下:
操作 111: 格式:1 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数加上 kkk;
操作 222: 格式:2 x 含义:输出第 xxx 个数的值。
输出格式
输出包含若干行整数,即为所有操作 222 的结果。
输入 #1
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
输出 #1
6
10
说明/提示
样例 1 解释:
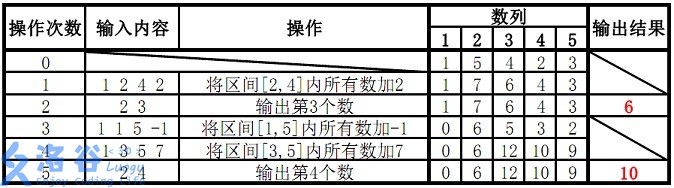
故输出结果为 666 和 101010。
数据规模与约定
对于 30%30\%30% 的数据:N≤8N\le8N≤8,M≤10M\le10M≤10;
对于 70%70\%70% 的数据:N≤10000N\le 10000N≤10000,M≤10000M\le10000M≤10000;
对于 100%100\%100% 的数据:1≤N,M≤5000001 \leq N, M\le 5000001≤N,M≤500000,1≤x,y≤n1 \leq x, y \leq n1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 2302^{30}230。
该模板题考察的是:区间 [x, y] 加 k以及查询第 x 个数的值
AC代码
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
int n,m,a[N],s[N],op,x,y,k;
int lowbit(int x)
{return x&-x;
}
void change(int x,int k)//单点修改(差分数组)
{ while(x<=n){s[x]+=k;x+=lowbit(x);}
}
int ask(int x)//前缀查询
{int ans=0;while(x>0){ans+=s[x];x-=lowbit(x);}return ans;
}
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)change(i,a[i]-a[i-1]);//初始化差分数组的树状数组while(m--){cin>>op>>x;if(op==1)//[x,y]区间+k {cin>>y>>k;change(x,k);change(y+1,-k);}else cout<<ask(x)<<endl;//查询第x个数的值=原始a[x]+差分数组前缀和。 }
}
signed main()
{IOS;int _=1;
// cin>>_;while(_--)solve();return 0;
}