《算法导论》第 31 章 - 数论算法
数论是计算机科学和密码学的基础,《算法导论》第 31 章系统介绍了数论算法的核心内容。本文将结合代码实现,详细讲解这些重要算法,帮助读者理解并掌握数论在计算机科学中的应用。
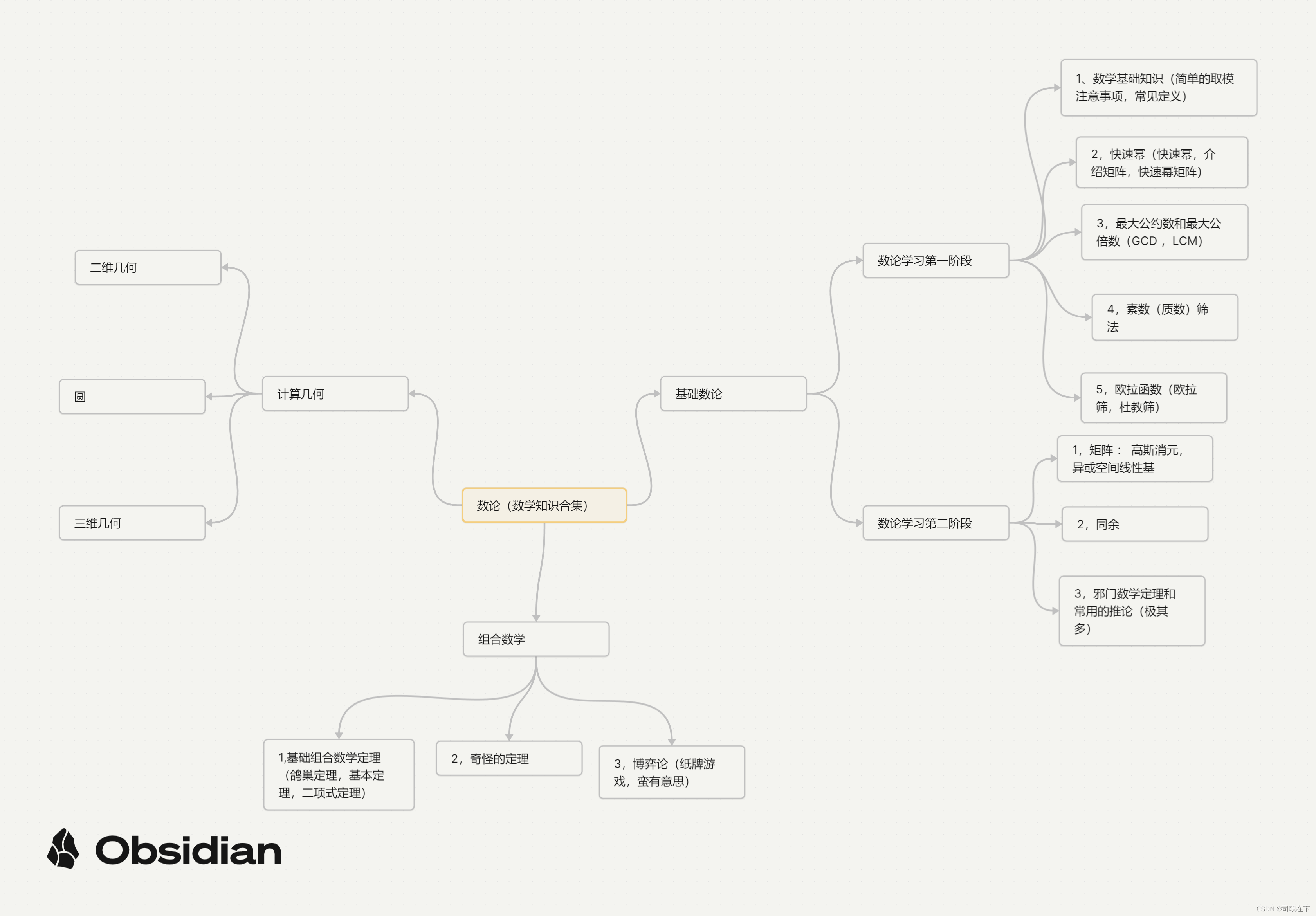
思维导图


31.1 基础数论概念
数论是研究整数性质的数学分支,在计算机科学中有广泛应用,特别是在密码学领域。
基本概念
- 整除性:如果 a 和 b 是整数且 a≠0,若存在整数 k 使得 b=ak,则称 a 整除 b,记为 a|b。
- 素数:大于 1 的整数,除了 1 和自身外没有其他正约数。
- 合数:大于 1 的非素数整数。
- 除法定理:对于任何整数 a 和正整数 n,存在唯一整数 q 和 r,使得 0≤r<n 且 a=qn+r。
代码示例:基础数论操作
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;// 判断a是否整除b
bool isDivisible(int a, int b) {if (a == 0) return false; // 避免除零错误return b % a == 0;
}// 判断一个数是否为素数
bool isPrime(int n) {if (n <= 1) return false; // 小于等于1的数不是素数if (n <= 3) return true; // 2和3是素数// 排除能被2或3整除的数if (n % 2 == 0 || n % 3 == 0) return false;// 检查到sqrt(n),步长为6for (int i = 5; i * i <= n; i += 6) {if (n % i == 0 || n % (i + 2) == 0)return false;}return true;
}// 找出n的所有约数
vector<int> findDivisors(int n) {vector<int> divisors;for (int i = 1; i * i <= n; ++i) {if (n % i == 0) {divisors.push_back(i);if (i != n / i) {divisors.push_back(n / i);}}}return divisors;
}// 实现除法定理,返回商和余数
pair<int, int> divisionTheorem(int a, int n) {if (n <= 0) {cerr << "n必须是正整数" << endl;return {0, 0};}int q = a / n;int r = a % n;// 确保余数为非负数if (r < 0) {q -= 1;r += n;}return {q, r};
}int main() {// 测试整除性int a = 3, b = 12;cout << a << (isDivisible(a, b) ? " 整除 " : " 不整除 ") << b << endl;// 测试素数判断int num = 17;cout << num << (isPrime(num) ? " 是素数" : " 不是素数") << endl;// 测试约数查找int n = 36;vector<int> divisors = findDivisors(n);cout << n << " 的所有约数:";for (int d : divisors) {cout << d << " ";}cout << endl;// 测试除法定理int a_val = 17, n_val = 5;auto [q, r] = divisionTheorem(a_val, n_val);cout << a_val << " = " << q << " * " << n_val << " + " << r << endl;return 0;
}
代码说明
上面的代码实现了几个基础的数论操作:
isDivisible函数判断一个数是否能整除另一个数isPrime函数高效判断一个数是否为素数findDivisors函数找出一个数的所有约数divisionTheorem函数实现除法定理,返回商和余数
这些基础操作是后续更复杂数论算法的基础。
31.2 最大公约数

最大公约数(GCD)是数论中的一个核心概念,指两个或多个整数共有约数中最大的一个。
欧几里得算法
欧几里得算法(也称辗转相除法)是求最大公约数的高效算法,基于以下原理:
对于任意非负整数 a 和正整数 b,有 gcd (a, b) = gcd (b, a mod b)
流程图:欧几里得算法
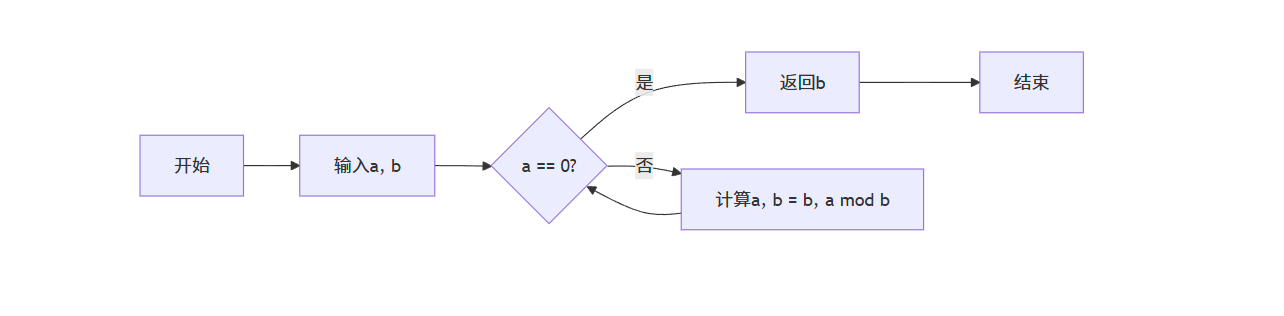
扩展欧几里得算法
扩展欧几里得算法不仅能计算 gcd (a, b),还能找到整数 x 和 y,使得:ax + by = gcd (a, b)
代码示例:最大公约数算法
#include <iostream>
#include <tuple>
using namespace std;// 欧几里得算法求最大公约数
int gcd(int a, int b) {while (b != 0) {int temp = b;b = a % b;a = temp;}return a;
}// 递归版本的欧几里得算法
int gcdRecursive(int a, int b) {if (b == 0)return a;return gcdRecursive(b, a % b);
}// 扩展欧几里得算法
// 返回 (gcd, x, y),满足 a*x + b*y = gcd
tuple<int, int, int> extendedGcd(int a, int b) {if (b == 0) {return {a, 1, 0};} else {auto [g, x, y] = extendedGcd(b, a % b);return {g, y, x - (a / b) * y};}
}// 求最小公倍数:lcm(a,b) = |a*b| / gcd(a,b)
int lcm(int a, int b) {if (a == 0 || b == 0)return 0;return (abs(a) / gcd(a, b)) * abs(b);
}int main() {int a = 48, b = 18;// 测试欧几里得算法cout << "gcd(" << a << ", " << b << ") = " << gcd(a, b) << endl;cout << "递归版 gcd(" << a << ", " << b << ") = " << gcdRecursive(a, b) << endl;// 测试扩展欧几里得算法auto [g, x, y] = extendedGcd(a, b);cout << "扩展欧几里得:" << a << "*" << x << " + " << b << "*" << y << " = " << g << endl;// 测试最小公倍数cout << "lcm(" << a << ", " << b << ") = " << lcm(a, b) << endl;// 更多测试案例int c = 105, d = 252;cout << "\ngcd(" << c << ", " << d << ") = " << gcd(c, d) << endl;auto [g2, x2, y2] = extendedGcd(c, d);cout << "扩展欧几里得:" << c << "*" << x2 << " + " << d << "*" << y2 << " = " << g2 << endl;cout << "验证:" << c << "*" << x2 << " + " << d << "*" << y2 << " = " << c*x2 + d*y2 << endl;return 0;
}
代码说明
上面的代码实现了:
- 迭代版本的欧几里得算法
- 递归版本的欧几里得算法
- 扩展欧几里得算法,能找到满足 ax + by = gcd (a,b) 的 x 和 y
- 基于 GCD 计算最小公倍数(LCM)的函数
扩展欧几里得算法在后续的模线性方程求解和密码学算法中有重要应用。
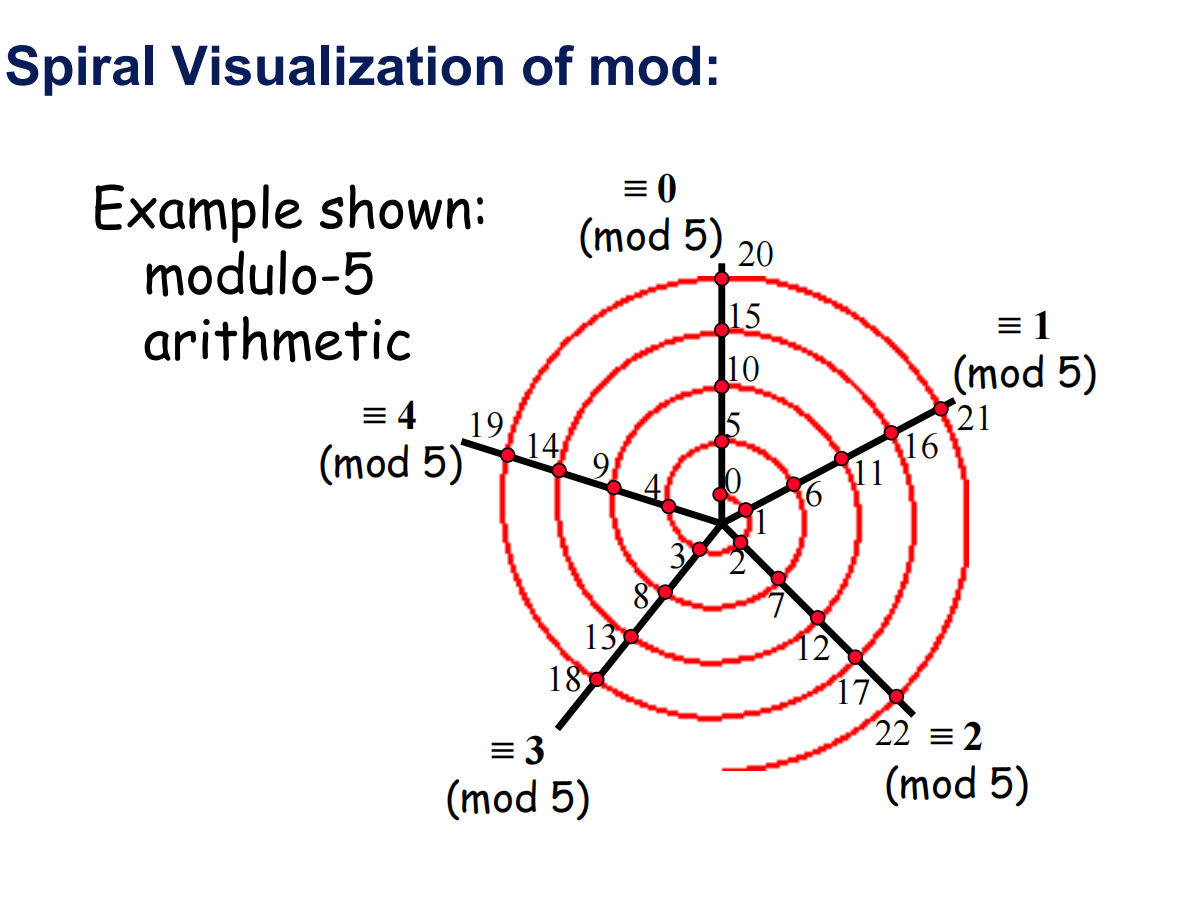
31.3 模运算
模运算在计算机科学中应用广泛,特别是在密码学、哈希算法和伪随机数生成等领域。
基本概念
- 模运算:a mod n 表示 a 除以 n 的余数,即 a = qn + r,其中 0 ≤ r < n,则 r = a mod n
- 同余:如果 a mod n = b mod n,则称 a 和 b 模 n 同余,记为 a ≡ b (mod n)
- 模算术:模运算下的加法、减法和乘法运算
模运算性质
- (a + b) mod n = [(a mod n) + (b mod n)] mod n
- (a - b) mod n = [(a mod n) - (b mod n) + n] mod n
- (a * b) mod n = [(a mod n) * (b mod n)] mod n
- 如果 a ≡ b (mod n) 且 c ≡ d (mod n),则:
- a + c ≡ b + d (mod n)
- a - c ≡ b - d (mod n)
- a * c ≡ b * d (mod n)
代码示例:模运算实现
#include <iostream>
using namespace std;// 确保结果为非负的模运算
int mod(int a, int n) {int result = a % n;if (result < 0) {result += n;}return result;
}// 模加法
int modAdd(int a, int b, int n) {return mod(mod(a, n) + mod(b, n), n);
}// 模减法
int modSubtract(int a, int b, int n) {return mod(mod(a, n) - mod(b, n), n);
}// 模乘法
int modMultiply(int a, int b, int n) {return mod((long long)mod(a, n) * mod(b, n), n);
}// 检查a和b是否模n同余
bool isCongruent(int a, int b, int n) {return mod(a, n) == mod(b, n);
}int main() {int a = 17, b = 5, n = 7;cout << "基本模运算示例:" << endl;cout << a << " mod " << n << " = " << mod(a, n) << endl;cout << b << " mod " << n << " = " << mod(b, n) << endl;cout << "\n模运算性质验证:" << endl;cout << "(" << a << " + " << b << ") mod " << n << " = " << mod(a + b, n) << endl;cout << "模加法实现:" << modAdd(a, b, n) << endl;cout << "\n(" << a << " - " << b << ") mod " << n << " = " << mod(a - b, n) << endl;cout << "模减法实现:" << modSubtract(a, b, n) << endl;cout << "\n(" << a << " * " << b << ") mod " << n << " = " << mod(a * b, n) << endl;cout << "模乘法实现:" << modMultiply(a, b, n) << endl;// 测试负数模运算int c = -13, m = 5;cout << "\n负数模运算:" << c << " mod " << m << " = " << mod(c, m) << endl;// 测试同余性int x = 25, y = 37, mod_val = 12;cout << "\n" << x << " 和 " << y << " 是否模 " << mod_val << " 同余? ";cout << (isCongruent(x, y, mod_val) ? "是" : "否") << endl;cout << x << " mod " << mod_val << " = " << mod(x, mod_val) << endl;cout << y << " mod " << mod_val << " = " << mod(y, mod_val) << endl;return 0;
}
代码说明
这段代码实现了模运算的基本操作,并验证了模运算的重要性质:
mod函数确保返回非负的余数,处理了负数情况modAdd、modSubtract、modMultiply分别实现了模加法、模减法和模乘法isCongruent函数检查两个数是否模 n 同余
模运算在密码学和计算机安全领域有广泛应用,是后续学习更复杂加密算法的基础。
31.4 求解模线性方程

模线性方程是形如 ax ≡ b (mod n) 的方程,求解这类方程在密码学和编码理论中有重要应用。
求解条件
方程 ax ≡ b (mod n) 有解的充分必要条件是 gcd (a, n) 整除 b。
如果 d = gcd (a, n) 且 d 整除 b,则方程有 d 个不同的解(模 n)。
求解步骤
- 计算 d = gcd (a, n)
- 检查 d 是否整除 b,若不整除则无解
- 否则,使用扩展欧几里得算法找到 x₀,使得 ax₀ + ny₀ = d
- 方程的一个特解为 x₀' = x₀ * (b/d) mod n
- 通解为 x = x₀' + k*(n/d) mod n,其中 k = 0, 1, ..., d-1
代码示例:求解模线性方程
#include <iostream>
using namespace std;// 确保结果为非负的模运算
int mod(int a, int n) {int result = a % n;if (result < 0) {result += n;}return result;
}// 模加法
int modAdd(int a, int b, int n) {return mod(mod(a, n) + mod(b, n), n);
}// 模减法
int modSubtract(int a, int b, int n) {return mod(mod(a, n) - mod(b, n), n);
}// 模乘法
int modMultiply(int a, int b, int n) {return mod((long long)mod(a, n) * mod(b, n), n);
}// 检查a和b是否模n同余
bool isCongruent(int a, int b, int n) {return mod(a, n) == mod(b, n);
}int main() {int a = 17, b = 5, n = 7;cout << "基本模运算示例:" << endl;cout << a << " mod " << n << " = " << mod(a, n) << endl;cout << b << " mod " << n << " = " << mod(b, n) << endl;cout << "\n模运算性质验证:" << endl;cout << "(" << a << " + " << b << ") mod " << n << " = " << mod(a + b, n) << endl;cout << "模加法实现:" << modAdd(a, b, n) << endl;cout << "\n(" << a << " - " << b << ") mod " << n << " = " << mod(a - b, n) << endl;cout << "模减法实现:" << modSubtract(a, b, n) << endl;cout << "\n(" << a << " * " << b << ") mod " << n << " = " << mod(a * b, n) << endl;cout << "模乘法实现:" << modMultiply(a, b, n) << endl;// 测试负数模运算int c = -13, m = 5;cout << "\n负数模运算:" << c << " mod " << m << " = " << mod(c, m) << endl;// 测试同余性int x = 25, y = 37, mod_val = 12;cout << "\n" << x << " 和 " << y << " 是否模 " << mod_val << " 同余? ";cout << (isCongruent(x, y, mod_val) ? "是" : "否") << endl;cout << x << " mod " << mod_val << " = " << mod(x, mod_val) << endl;cout << y << " mod " << mod_val << " = " << mod(y, mod_val) << endl;return 0;
}
代码说明
这段代码实现了模线性方程 ax ≡ b (mod n) 的求解:
- 利用扩展欧几里得算法找到方程的一个特解
- 根据解的存在条件判断方程是否有解
- 如果有解,计算并返回所有不同的解(模 n)
- 对解进行了验证,确保其正确性
模线性方程的求解是很多密码学算法的基础,例如在密钥生成和加密解密过程中都有应用。
31.5 中国余数定理
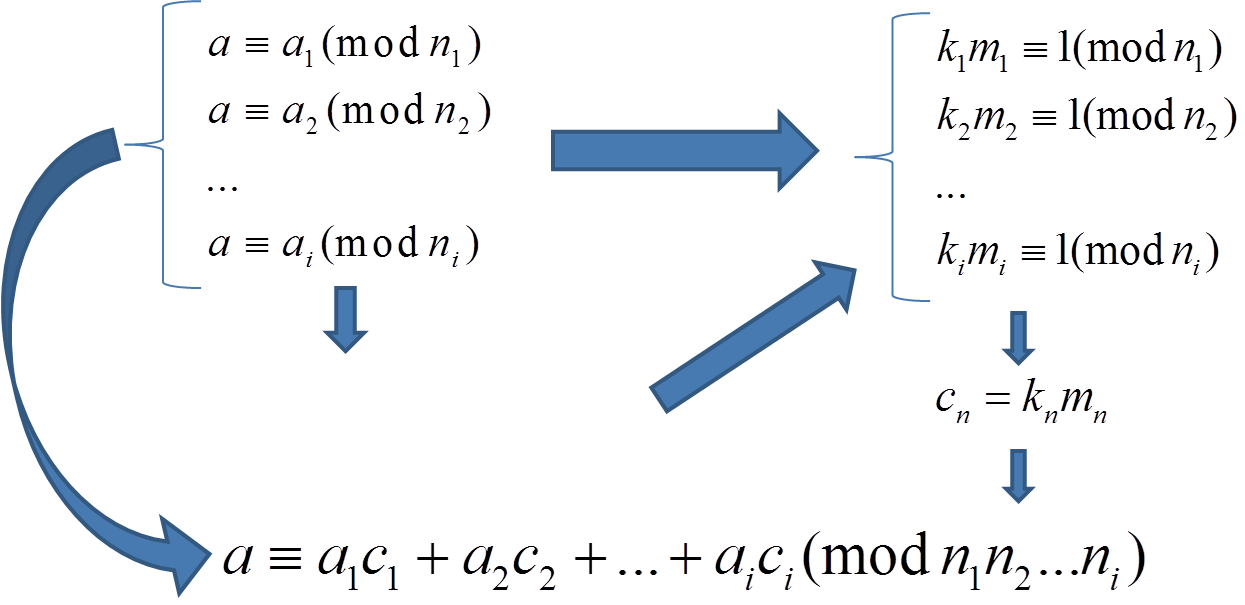
中国余数定理(CRT)是数论中的一个重要定理,最早见于《孙子算经》,它提供了一种求解同余方程组的方法。
定理表述
如果 n₁, n₂, ..., nₖ是两两互素的正整数,那么对于任意整数 a₁, a₂, ..., aₖ,方程组:
x ≡ a₁ (mod n₁)
x ≡ a₂ (mod n₂)
...
x ≡ aₖ (mod nₖ)
存在唯一解模 N = n₁・n₂・...・nₖ。
求解方法
- 计算 N = n₁・n₂・...・nₖ
- 对于每个 i,计算 mᵢ = N /nᵢ
- 对于每个 i,计算 mᵢ的逆元 mᵢ⁻¹ 模 nᵢ,即 mᵢ・mᵢ⁻¹ ≡ 1 (mod nᵢ)
- 解为 x = (a₁・m₁・m₁⁻¹ + a₂・m₂・m₂⁻¹ + ... + aₖ・mₖ・mₖ⁻¹) mod N
代码示例:中国余数定理的实现
#include <iostream>
#include <vector>
#include <tuple>
#include <numeric> // for accumulate
using namespace std;// 计算两个数的最大公约数
long long gcd(long long a, long long b) {while (b != 0) {long long temp = b;b = a % b;a = temp;}return a;
}// 扩展欧几里得算法
// 返回 (gcd, x, y),满足 a*x + b*y = gcd
tuple<long long, long long, long long> extendedGcd(long long a, long long b) {if (b == 0) {return {a, 1, 0};} else {auto [g, x, y] = extendedGcd(b, a % b);return {g, y, x - (a / b) * y};}
}// 计算模n下a的逆元,如果不存在则返回-1
long long modInverse(long long a, long long n) {auto [g, x, y] = extendedGcd(a, n);if (g != 1) {return -1; // 逆元不存在} else {// 确保逆元为正数return (x % n + n) % n;}
}// 确保结果为非负的模运算
long long mod(long long a, long long n) {long long result = a % n;if (result < 0) {result += n;}return result;
}// 中国余数定理求解同余方程组
// 方程组形式:x ≡ a_i (mod n_i)
// 返回值:(x, N),其中x是解,N是模,如果无解则x = -1
pair<long long, long long> chineseRemainderTheorem(const vector<long long>& a, const vector<long long>& n) {// 检查输入是否有效if (a.size() != n.size()) {return {-1, 0}; // 输入不匹配}int k = a.size();if (k == 0) {return {0, 1}; // 空方程组,平凡解}// 检查模数是否两两互素for (int i = 0; i < k; ++i) {for (int j = i + 1; j < k; ++j) {if (gcd(n[i], n[j]) != 1) {return {-1, 0}; // 模数不是两两互素,CRT不适用}}}// 计算N = n₁·n₂·...·nₖlong long N = 1;for (long long ni : n) {N *= ni;}// 计算解xlong long x = 0;for (int i = 0; i < k; ++i) {long long mi = N / n[i]; // m_i = N / n_ilong long inv_mi = modInverse(mi, n[i]); // m_i的逆元模n_iif (inv_mi == -1) {return {-1, 0}; // 逆元不存在,无法求解}// x += a_i * m_i * inv_m_ix += a[i] * mi * inv_mi;x = mod(x, N); // 保持x在模N范围内}return {x, N};
}// 验证解是否满足所有同余方程
bool verifySolution(long long x, const vector<long long>& a, const vector<long long>& n) {for (int i = 0; i < a.size(); ++i) {if (mod(x, n[i]) != mod(a[i], n[i])) {return false;}}return true;
}int main() {// 示例1:《孙子算经》中的问题// 今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?// 即求解:// x ≡ 2 (mod 3)// x ≡ 3 (mod 5)// x ≡ 2 (mod 7)vector<long long> a1 = {2, 3, 2};vector<long long> n1 = {3, 5, 7};auto [x1, N1] = chineseRemainderTheorem(a1, n1);cout << "示例1求解结果:" << endl;if (x1 == -1) {cout << "方程组无解" << endl;} else {cout << "解为:x ≡ " << x1 << " (mod " << N1 << ")" << endl;cout << "最小正整数解:" << x1 << endl;cout << "验证结果:" << (verifySolution(x1, a1, n1) ? "正确" : "错误") << endl;}// 示例2:另一个同余方程组// x ≡ 1 (mod 2)// x ≡ 2 (mod 3)// x ≡ 3 (mod 5)vector<long long> a2 = {1, 2, 3};vector<long long> n2 = {2, 3, 5};auto [x2, N2] = chineseRemainderTheorem(a2, n2);cout << "\n示例2求解结果:" << endl;if (x2 == -1) {cout << "方程组无解" << endl;} else {cout << "解为:x ≡ " << x2 << " (mod " << N2 << ")" << endl;cout << "最小正整数解:" << x2 << endl;cout << "验证结果:" << (verifySolution(x2, a2, n2) ? "正确" : "错误") << endl;}// 示例3:模数不互素的情况(无解)vector<long long> a3 = {2, 3};vector<long long> n3 = {4, 6}; // gcd(4,6)=2≠1,不互素auto [x3, N3] = chineseRemainderTheorem(a3, n3);cout << "\n示例3求解结果:" << endl;if (x3 == -1) {cout << "方程组无解(模数不互素)" << endl;} else {cout << "解为:x ≡ " << x3 << " (mod " << N3 << ")" << endl;}return 0;
}

代码说明
这段代码实现了中国余数定理的求解过程:
- 首先验证输入的同余方程组是否满足 CRT 的条件(模数两两互素)
- 计算所有模数的乘积 N
- 对于每个方程,计算相应的 mᵢ和其逆元
- 组合这些值得到方程组的解 x
- 提供了验证函数,检查解是否满足所有同余方程
中国余数定理在密码学、编码理论和分布式计算等领域有重要应用,例如在 RSA 加密算法中就用到了 CRT 来提高解密效率。
31.6 元素的幂
计算元素的幂,特别是模指数运算,是很多密码学算法的核心操作。直接计算大指数的幂会导致数值过大,因此需要高效的算法。
快速幂算法
快速幂算法(也称反复平方算法)利用指数的二进制表示,将计算 a^b 的时间复杂度从 O (b) 降低到 O (log b)。
基本思想:
- 如果 b 是偶数,a^b = (a^(b/2))^2
- 如果 b 是奇数,a^b = a * (a^((b-1)/2))^2
模指数运算
在密码学中,我们经常需要计算 a^b mod n,直接计算 a^b 再取模会导致数值过大,因此可以利用模运算的性质:
(a * b) mod n = [(a mod n) * (b mod n)] mod n
结合快速幂算法,可以高效计算模指数。
代码示例:快速幂与模指数运算
#include <iostream>
#include <cmath>
using namespace std;// 普通幂运算(用于对比)
long long powerNaive(long long a, long long b) {long long result = 1;for (int i = 0; i < b; ++i) {result *= a;}return result;
}// 快速幂算法:计算a^b
long long powerFast(long long a, long long b) {long long result = 1;long long base = a;while (b > 0) {// 如果b是奇数,将当前base乘到result中if (b % 2 == 1) {result *= base;}// base自乘,b除以2base *= base;b /= 2;}return result;
}// 模运算:确保结果为非负
long long mod(long long a, long long n) {long long result = a % n;if (result < 0) {result += n;}return result;
}// 快速模指数运算:计算(a^b) mod n
long long modPower(long long a, long long b, long long n) {long long result = 1;long long base = mod(a, n); // 确保base在模n范围内while (b > 0) {// 如果b是奇数,将当前base乘到result中,并取模if (b % 2 == 1) {result = mod(result * base, n);}// base自乘并取模,b除以2base = mod(base * base, n);b /= 2;}return result;
}int main() {// 测试快速幂算法long long a = 3, b = 5;cout << "测试快速幂算法:" << endl;cout << a << "^" << b << " = " << powerNaive(a, b) << " (普通方法)" << endl;cout << a << "^" << b << " = " << powerFast(a, b) << " (快速幂方法)" << endl;// 测试更大的指数a = 2;b = 10;cout << "\n" << a << "^" << b << " = " << powerNaive(a, b) << " (普通方法)" << endl;cout << a << "^" << b << " = " << powerFast(a, b) << " (快速幂方法)" << endl;// 测试模指数运算a = 7;b = 5;long long n = 13;cout << "\n测试模指数运算:" << endl;cout << a << "^" << b << " mod " << n << " = " << mod(powerFast(a, b), n) << " (先求幂再取模)" << endl;cout << a << "^" << b << " mod " << n << " = " << modPower(a, b, n) << " (快速模指数方法)" << endl;// 测试更大的指数a = 12345;b = 9876;n = 1000000007;cout << "\n大指数测试:" << endl;cout << a << "^" << b << " mod " << n << " = " << modPower(a, b, n) << endl;// 测试负数情况a = -3;b = 4;n = 5;cout << "\n负数测试:" << endl;cout << a << "^" << b << " mod " << n << " = " << modPower(a, b, n) << endl;return 0;
}
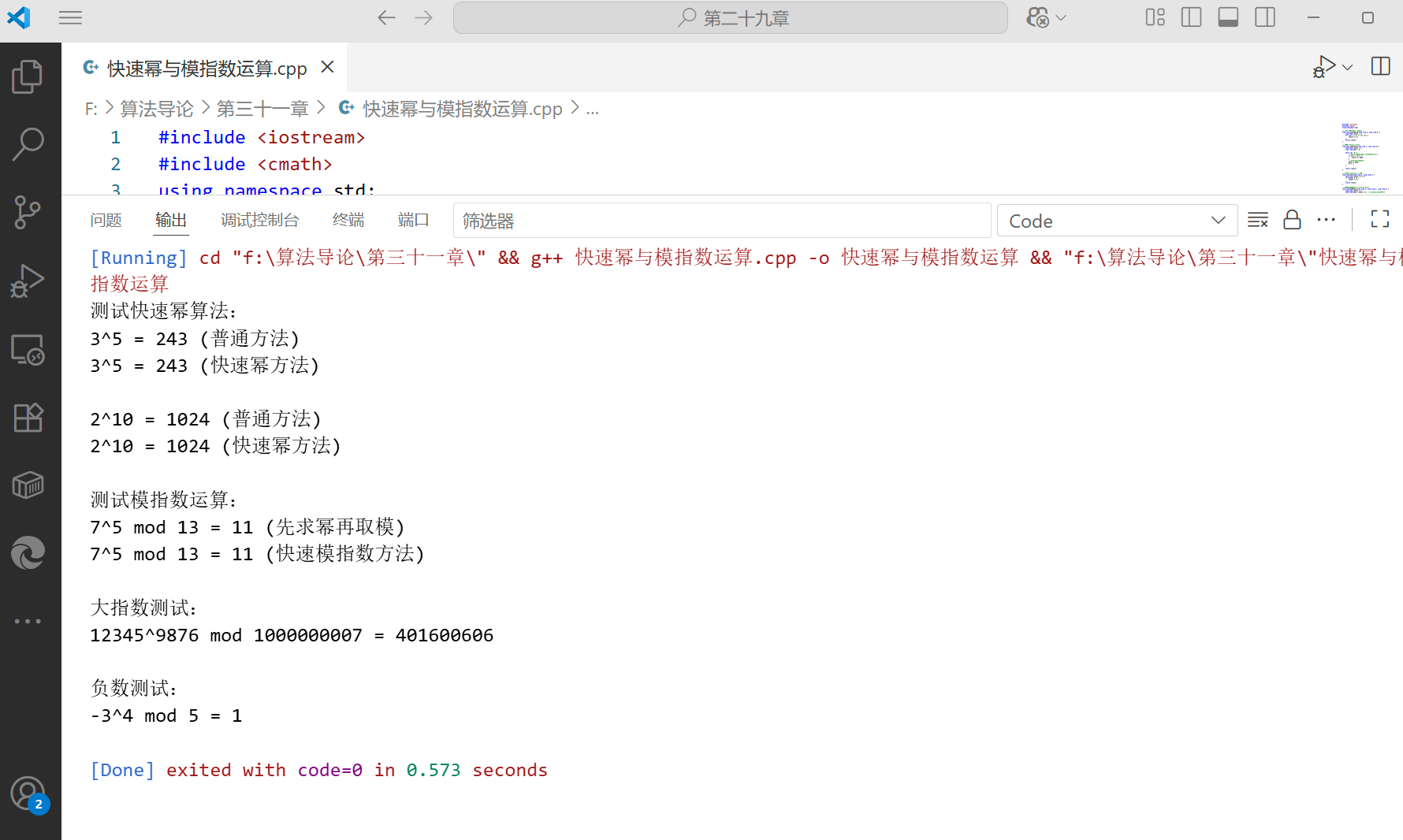
代码说明
这段代码实现了高效的幂运算和模指数运算:
powerNaive:普通的幂运算,时间复杂度 O (b)powerFast:快速幂算法,利用指数的二进制表示,时间复杂度 O (log b)modPower:快速模指数运算,结合快速幂和模运算的性质,高效计算 (a^b) mod n
模指数运算在密码学中应用广泛,如 RSA、Diffie-Hellman 密钥交换等算法的核心操作都依赖于高效的模指数运算。
31.7 RSA 公钥加密系统
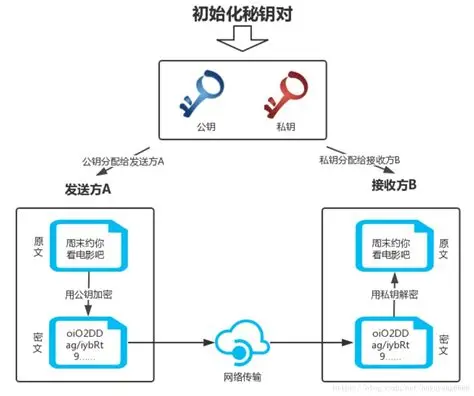
RSA 是一种非对称加密算法,由 Ron Rivest、Adi Shamir 和 Leonard Adleman 于 1977 年提出。它使用一对密钥:公钥(公开)和私钥(保密),公钥用于加密,私钥用于解密。
RSA 算法步骤
密钥生成:
- 选择两个不同的大素数 p 和 q
- 计算 n = p * q
- 计算欧拉函数 φ(n) = (p-1) * (q-1)
- 选择整数 e,使得 1 <e < φ(n) 且 gcd (e, φ(n)) = 1
- 计算 e 的逆元 d,使得 (e * d) ≡ 1 (mod φ(n))
- 公钥为 (e, n),私钥为 (d, n)
加密:
- 明文 m 必须满足 0 ≤ m < n
- 密文 c = m^e mod n
解密:
- 明文 m = c^d mod n
代码示例:RSA 加密系统的实现
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <algorithm>
#include <tuple> // 添加tuple头文件
using namespace std;// 计算最大公约数
long long gcd(long long a, long long b) {while (b != 0) {long long temp = b;b = a % b;a = temp;}return a;
}// 扩展欧几里得算法
tuple<long long, long long, long long> extendedGcd(long long a, long long b) {if (b == 0) {return make_tuple(a, 1, 0); // 使用make_tuple创建元组} else {auto result = extendedGcd(b, a % b);long long g = get<0>(result);long long x = get<1>(result);long long y = get<2>(result);return make_tuple(g, y, x - (a / b) * y); // 不使用结构化绑定}
}// 计算模n下a的逆元
long long modInverse(long long a, long long n) {auto result = extendedGcd(a, n);long long g = get<0>(result);long long x = get<1>(result);long long y = get<2>(result);if (g != 1) {return -1; // 逆元不存在} else {return (x % n + n) % n;}
}// 模运算:确保结果为非负
long long mod(long long a, long long n) {long long result = a % n;if (result < 0) {result += n;}return result;
}// 快速模指数运算:(a^b) mod n
long long modPower(long long a, long long b, long long n) {long long result = 1;a = mod(a, n);while (b > 0) {if (b % 2 == 1) {result = mod(result * a, n);}a = mod(a * a, n);b /= 2;}return result;
}// Miller-Rabin素数测试
bool isPrime(long long n, int k = 5) {if (n <= 1) return false;if (n <= 3) return true;if (n % 2 == 0) return false;// 将n-1表示为d*2^slong long d = n - 1;int s = 0;while (d % 2 == 0) {d /= 2;s++;}// 进行k次测试for (int i = 0; i < k; i++) {long long a = 2 + rand() % (n - 3); // 随机选择a ∈ [2, n-2]long long x = modPower(a, d, n);if (x == 1 || x == n - 1) {continue;}for (int j = 0; j < s - 1; j++) {x = modPower(x, 2, n);if (x == n - 1) {goto nextTest;}}return false; // 确定不是素数nextTest:;}return true; // 可能是素数
}// 生成指定范围内的随机素数
long long generatePrime(long long min, long long max) {while (true) {long long p = min + rand() % (max - min + 1);// 确保是奇数if (p % 2 == 0) {p++;if (p > max) continue;}if (isPrime(p)) {return p;}}
}// RSA密钥对结构
struct RSAKeyPair {long long publicExponent; // elong long privateExponent; // dlong long modulus; // n
};// 生成RSA密钥对
RSAKeyPair generateRSAKeys(long long minPrime, long long maxPrime) {RSAKeyPair keys;// 生成两个不同的素数p和qlong long p, q;do {p = generatePrime(minPrime, maxPrime);q = generatePrime(minPrime, maxPrime);} while (p == q);// 计算n = p*qkeys.modulus = p * q;// 计算欧拉函数φ(n) = (p-1)*(q-1)long long phi = (p - 1) * (q - 1);// 选择公钥e,满足1 < e < φ(n)且gcd(e, φ(n)) = 1do {keys.publicExponent = 2 + rand() % (phi - 3);} while (gcd(keys.publicExponent, phi) != 1);// 计算私钥d,e的逆元模φ(n)keys.privateExponent = modInverse(keys.publicExponent, phi);return keys;
}// RSA加密:c = m^e mod n
long long rsaEncrypt(long long m, long long e, long long n) {if (m < 0 || m >= n) {cerr << "明文必须满足 0 ≤ m < n" << endl;return -1;}return modPower(m, e, n);
}// RSA解密:m = c^d mod n
long long rsaDecrypt(long long c, long long d, long long n) {if (c < 0 || c >= n) {cerr << "密文必须满足 0 ≤ c < n" << endl;return -1;}return modPower(c, d, n);
}int main() {// 初始化随机数生成器srand(time(0));// 生成RSA密钥对(注意:实际应用中应使用更大的素数)cout << "生成RSA密钥对中..." << endl;RSAKeyPair keys = generateRSAKeys(100, 1000);cout << "\nRSA密钥对:" << endl;cout << "公钥 (e, n): (" << keys.publicExponent << ", " << keys.modulus << ")" << endl;cout << "私钥 (d, n): (" << keys.privateExponent << ", " << keys.modulus << ")" << endl;// 测试加密解密过程long long message;cout << "\n请输入要加密的明文(0 到 " << keys.modulus - 1 << " 之间的整数): ";cin >> message;// 加密long long ciphertext = rsaEncrypt(message, keys.publicExponent, keys.modulus);if (ciphertext != -1) {cout << "加密后的密文: " << ciphertext << endl;// 解密long long decryptedMessage = rsaDecrypt(ciphertext, keys.privateExponent, keys.modulus);if (decryptedMessage != -1) {cout << "解密后的明文: " << decryptedMessage << endl;// 验证解密是否正确if (decryptedMessage == message) {cout << "验证成功:解密后的明文与原始明文一致" << endl;} else {cout << "验证失败:解密后的明文与原始明文不一致" << endl;}}}return 0;
}
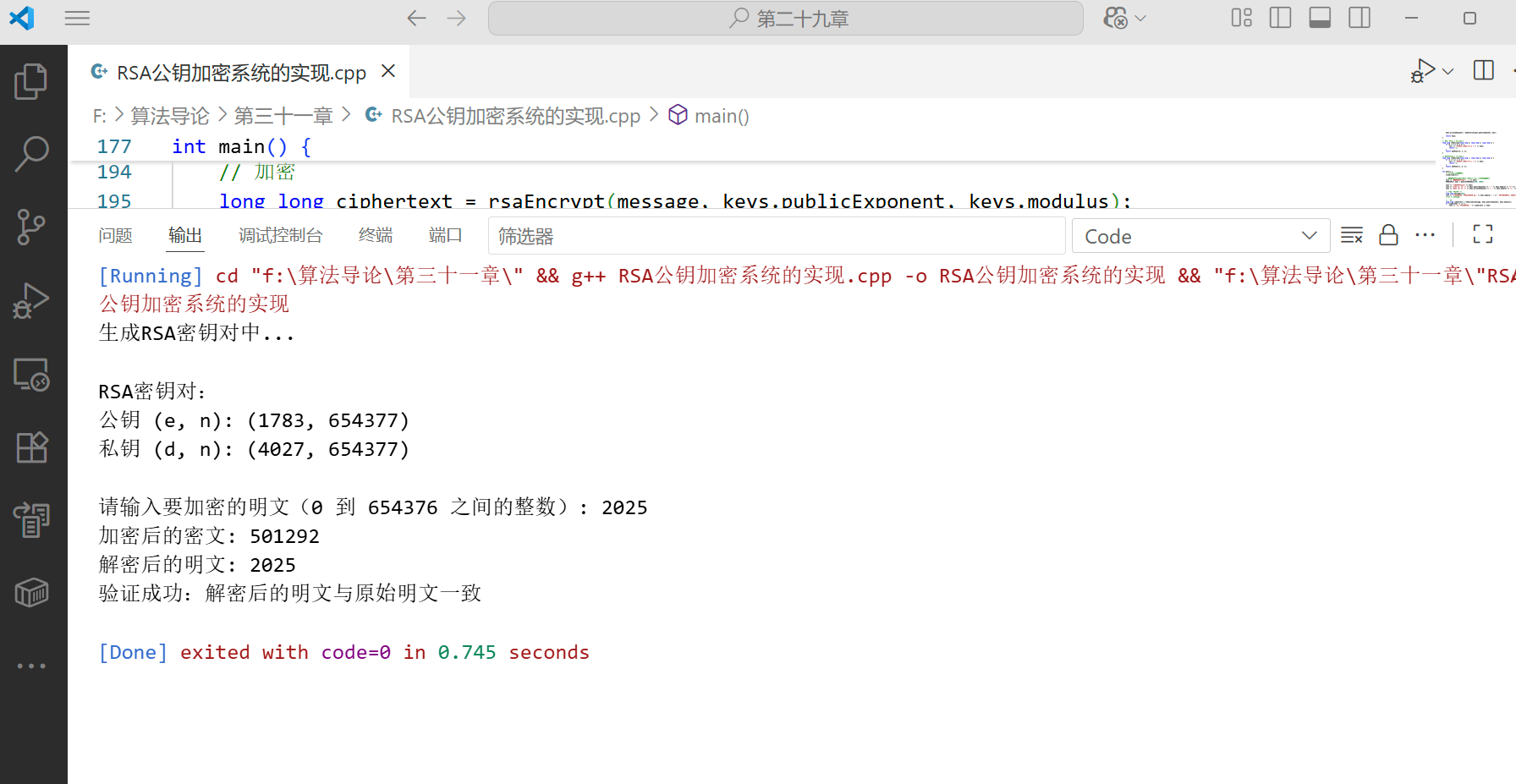
代码说明
这段代码实现了一个简化的 RSA 加密系统:
- 首先实现了 RSA 所需的辅助函数:gcd、扩展欧几里得算法、模逆元、快速模指数运算等
- 使用 Miller-Rabin 算法进行素数测试,用于生成大素数
- 实现了 RSA 密钥对生成过程:选择素数 p 和 q,计算 n 和 φ(n),选择 e 并计算 d
- 实现了加密函数(使用公钥)和解密函数(使用私钥)
注意:这个实现是为了演示 RSA 的基本原理,实际应用中需要使用更大的素数(通常是 1024 位或 2048 位)以确保安全性。
31.8 素数的测试
素数在密码学和计算机科学中有着重要应用,因此高效地判断一个数是否为素数至关重要。
素数测试方法
- 试除法:最简单但效率低的方法,检查从 2 到√n 的所有数是否能整除 n
- Miller-Rabin 素数测试:一种概率性测试,能高效判断一个数是否为素数
Miller-Rabin 算法原理
Miller-Rabin 测试基于费马小定理的一个变形:
如果 n 是一个奇素数,且 n-1 = d・2^s,那么对于任何与 n 互素的 a,要么 a^d ≡ 1 (mod n),要么存在某个 0 ≤ r < s 使得 a^(d・2^r) ≡ -1 (mod n)
算法步骤:
- 写出 n-1 = d・2^s
- 选择一个随机整数 a (1 < a < n)
- 计算 x = a^d mod n
- 如果 x = 1 或 x = n-1,则继续下一个 a
- 否则,重复 s-1 次:x = x² mod n,如果 x = n-1 则跳出并继续下一个 a
- 如果经过所有迭代后 x 仍不等于 n-1,则 n 是合数
- 对多个不同的 a 重复测试,若都通过则 n 很可能是素数
代码示例:素数测试算法
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cmath>
using namespace std;// 试除法判断素数
bool isPrimeTrialDivision(long long n) {if (n <= 1) return false;if (n <= 3) return true;if (n % 2 == 0 || n % 3 == 0) return false;// 检查到sqrt(n),步长为6for (long long i = 5; i * i <= n; i += 6) {if (n % i == 0 || n % (i + 2) == 0)return false;}return true;
}// 模运算:确保结果为非负
long long mod(long long a, long long n) {long long result = a % n;if (result < 0) {result += n;}return result;
}// 快速模指数运算:(a^b) mod n
long long modPower(long long a, long long b, long long n) {long long result = 1;a = mod(a, n);while (b > 0) {if (b % 2 == 1) {result = mod(result * a, n);}a = mod(a * a, n);b /= 2;}return result;
}// Miller-Rabin素数测试
// k是测试次数,次数越多准确率越高
bool isPrimeMillerRabin(long long n, int k = 5) {// 处理小数字的情况if (n <= 1) return false;if (n <= 3) return true;if (n % 2 == 0) return false;// 将n-1表示为d*2^slong long d = n - 1;int s = 0;while (d % 2 == 0) {d /= 2;s++;}// 进行k次测试for (int i = 0; i < k; i++) {// 随机选择a ∈ [2, n-2]long long a = 2 + rand() % (n - 3);long long x = modPower(a, d, n);if (x == 1 || x == n - 1) {continue;}bool possiblePrime = false;for (int j = 0; j < s - 1; j++) {x = modPower(x, 2, n);if (x == n - 1) {possiblePrime = true;break;}}if (!possiblePrime) {return false; // 确定不是素数}}return true; // 可能是素数
}// 比较两种算法的性能
void compareAlgorithms(long long maxNum) {cout << "\n比较试除法和Miller-Rabin算法的性能..." << endl;cout << "测试范围: 2 到 " << maxNum << endl;// 测试试除法clock_t start = clock();int countTrial = 0;for (long long i = 2; i <= maxNum; i++) {if (isPrimeTrialDivision(i)) {countTrial++;}}clock_t end = clock();double timeTrial = double(end - start) / CLOCKS_PER_SEC;// 测试Miller-Rabin算法start = clock();int countMiller = 0;for (long long i = 2; i <= maxNum; i++) {if (isPrimeMillerRabin(i, 5)) {countMiller++;}}end = clock();double timeMiller = double(end - start) / CLOCKS_PER_SEC;cout << "试除法找到 " << countTrial << " 个素数,耗时 " << timeTrial << " 秒" << endl;cout << "Miller-Rabin算法找到 " << countMiller << " 个素数,耗时 " << timeMiller << " 秒" << endl;cout << "Miller-Rabin算法比试除法快 " << timeTrial / timeMiller << " 倍" << endl;
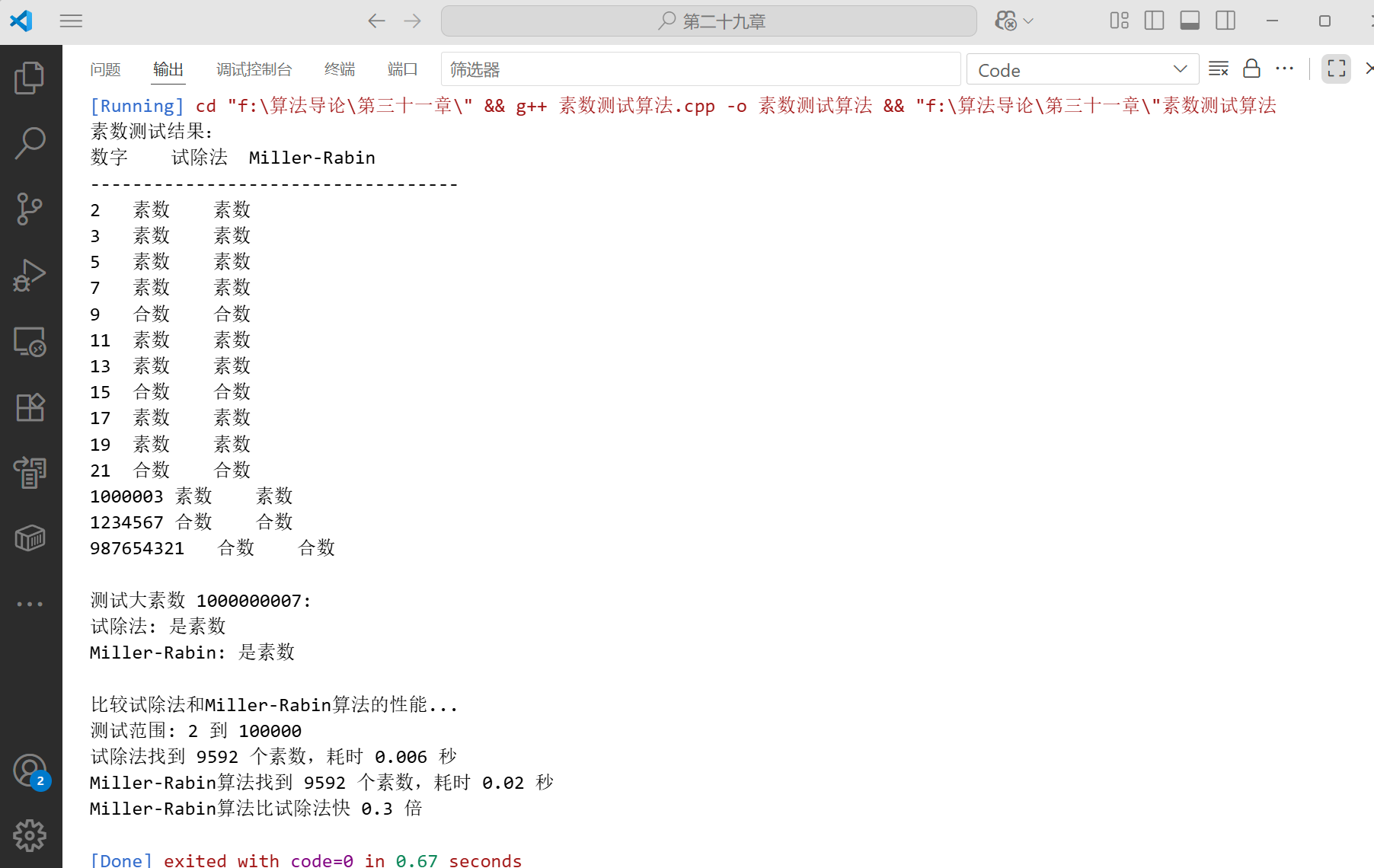
}int main() {// 初始化随机数生成器srand(time(0));// 测试几个已知的素数和合数long long numbers[] = {2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 1000003, 1234567, 987654321};int numCount = sizeof(numbers) / sizeof(numbers[0]);cout << "素数测试结果:" << endl;cout << "数字\t试除法\tMiller-Rabin" << endl;cout << "-----------------------------------" << endl;for (int i = 0; i < numCount; i++) {long long n = numbers[i];bool trial = isPrimeTrialDivision(n);bool miller = isPrimeMillerRabin(n, 5);cout << n << "\t" << (trial ? "素数" : "合数") << "\t" << (miller ? "素数" : "合数") << endl;}// 测试大素数long long largePrime = 1000000007; // 已知的大素数cout << "\n测试大素数 " << largePrime << ":" << endl;cout << "试除法: " << (isPrimeTrialDivision(largePrime) ? "是素数" : "不是素数") << endl;cout << "Miller-Rabin: " << (isPrimeMillerRabin(largePrime, 5) ? "是素数" : "不是素数") << endl;// 比较两种算法的性能compareAlgorithms(100000);return 0;
}
代码说明
这段代码实现了两种素数测试算法并进行了比较:
isPrimeTrialDivision:实现了优化的试除法,检查到√n,步长为 6isPrimeMillerRabin:实现了 Miller-Rabin 概率性素数测试
代码还包含了一个性能比较函数,展示了 Miller-Rabin 算法相比试除法的巨大优势,特别是对于大数字的测试。
在实际应用中,Miller-Rabin 算法通常与确定性测试结合使用,对于一定范围内的数字,可以使用特定的基数集合进行测试,以确保结果的准确性。
31.9 整数的因子分解
整数的因子分解是将一个正整数分解成几个素数的乘积的过程。这是数论中的一个重要问题,在密码学中有着特殊的意义(例如 RSA 的安全性基于大整数因子分解的困难性)。
因子分解算法
- 试除法:最简单的方法,尝试从 2 到√n 的所有可能因子
- Pollard's Rho 算法:一种概率性算法,能高效分解大整数
Pollard's Rho 算法原理
Pollard's Rho 算法是一种基于伪随机数生成的因子分解算法,其基本思想是:
- 对于待分解的 n,若 n 是偶数,则 2 是一个因子
- 否则,使用一个伪随机函数 f (x) = (x² + c) mod n 生成序列
- 使用 Floyd 的循环检测算法(龟兔赛跑算法)寻找序列中的碰撞
- 计算碰撞值之间的差与 n 的最大公约数,若结果是 1 或 n 则重新尝试,否则找到一个非平凡因子
代码示例:整数因子分解算法
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <algorithm>
using namespace std;// 计算最大公约数
long long gcd(long long a, long long b) {while (b != 0) {long long temp = b;b = a % b;a = temp;}return a;
}// 模运算:确保结果为非负
long long mod(long long a, long long n) {long long result = a % n;if (result < 0) {result += n;}return result;
}// 快速模指数运算:(a^b) mod n
long long modPower(long long a, long long b, long long n) {long long result = 1;a = mod(a, n);while (b > 0) {if (b % 2 == 1) {result = mod(result * a, n);}a = mod(a * a, n);b /= 2;}return result;
}// Miller-Rabin素数测试
bool isPrime(long long n, int k = 5) {if (n <= 1) return false;if (n <= 3) return true;if (n % 2 == 0) return false;long long d = n - 1;int s = 0;while (d % 2 == 0) {d /= 2;s++;}for (int i = 0; i < k; i++) {long long a = 2 + rand() % (n - 3);long long x = modPower(a, d, n);if (x == 1 || x == n - 1) {continue;}bool possiblePrime = false;for (int j = 0; j < s - 1; j++) {x = modPower(x, 2, n);if (x == n - 1) {possiblePrime = true;break;}}if (!possiblePrime) {return false;}}return true;
}// 试除法分解整数
vector<long long> trialDivision(long long n) {vector<long long> factors;// 处理2的情况while (n % 2 == 0) {factors.push_back(2);n /= 2;}// 处理奇数因子for (long long i = 3; i * i <= n; i += 2) {while (n % i == 0) {factors.push_back(i);n /= i;}}// 如果剩余的n是一个大于2的素数if (n > 1) {factors.push_back(n);}sort(factors.begin(), factors.end());return factors;
}// Pollard's Rho算法的辅助函数
long long pollardsRho(long long n) {if (n % 2 == 0) return 2;if (n % 3 == 0) return 3;if (n % 5 == 0) return 5;while (true) {long long c = 1 + rand() % (n - 1);auto f = [&](long long x) { return mod(mod(x * x, n) + c, n); };long long x = 2, y = 2, d = 1;long long q = 1;int steps = 0, maxSteps = 1 << 20;while (d == 1 && steps < maxSteps) {x = f(x);y = f(f(y));d = gcd(abs(x - y), n);steps++;}if (d != 1 && d != n) return d;}
}// 使用Pollard's Rho算法分解整数
void pollardsRhoFactor(long long n, vector<long long>& factors) {if (n == 1) return;if (isPrime(n)) {factors.push_back(n);return;}long long d = pollardsRho(n);pollardsRhoFactor(d, factors);pollardsRhoFactor(n / d, factors);
}// Pollard's Rho算法的包装函数
vector<long long> pollardsRhoFactorization(long long n) {vector<long long> factors;if (n <= 1) return factors;pollardsRhoFactor(n, factors);sort(factors.begin(), factors.end());return factors;
}// 打印因子分解结果
void printFactors(long long n, const vector<long long>& factors) {cout << n << " = ";if (factors.empty()) {cout << "1" << endl;return;}for (size_t i = 0; i < factors.size(); i++) {cout << factors[i];if (i != factors.size() - 1) {cout << " × ";}}cout << endl;
}// 比较两种算法的性能
void compareAlgorithms(long long n) {cout << "\n比较两种因子分解算法的性能..." << endl;cout << "分解数字: " << n << endl;// 测试试除法clock_t start = clock();vector<long long> factorsTrial = trialDivision(n);clock_t end = clock();double timeTrial = double(end - start) / CLOCKS_PER_SEC;// 测试Pollard's Rho算法start = clock();vector<long long> factorsRho = pollardsRhoFactorization(n);end = clock();double timeRho = double(end - start) / CLOCKS_PER_SEC;cout << "试除法结果: ";printFactors(n, factorsTrial);cout << "试除法耗时: " << timeTrial << " 秒" << endl;cout << "Pollard's Rho算法结果: ";printFactors(n, factorsRho);cout << "Pollard's Rho算法耗时: " << timeRho << " 秒" << endl;if (timeRho > 0) {cout << "Pollard's Rho算法比试除法快 " << timeTrial / timeRho << " 倍" << endl;}
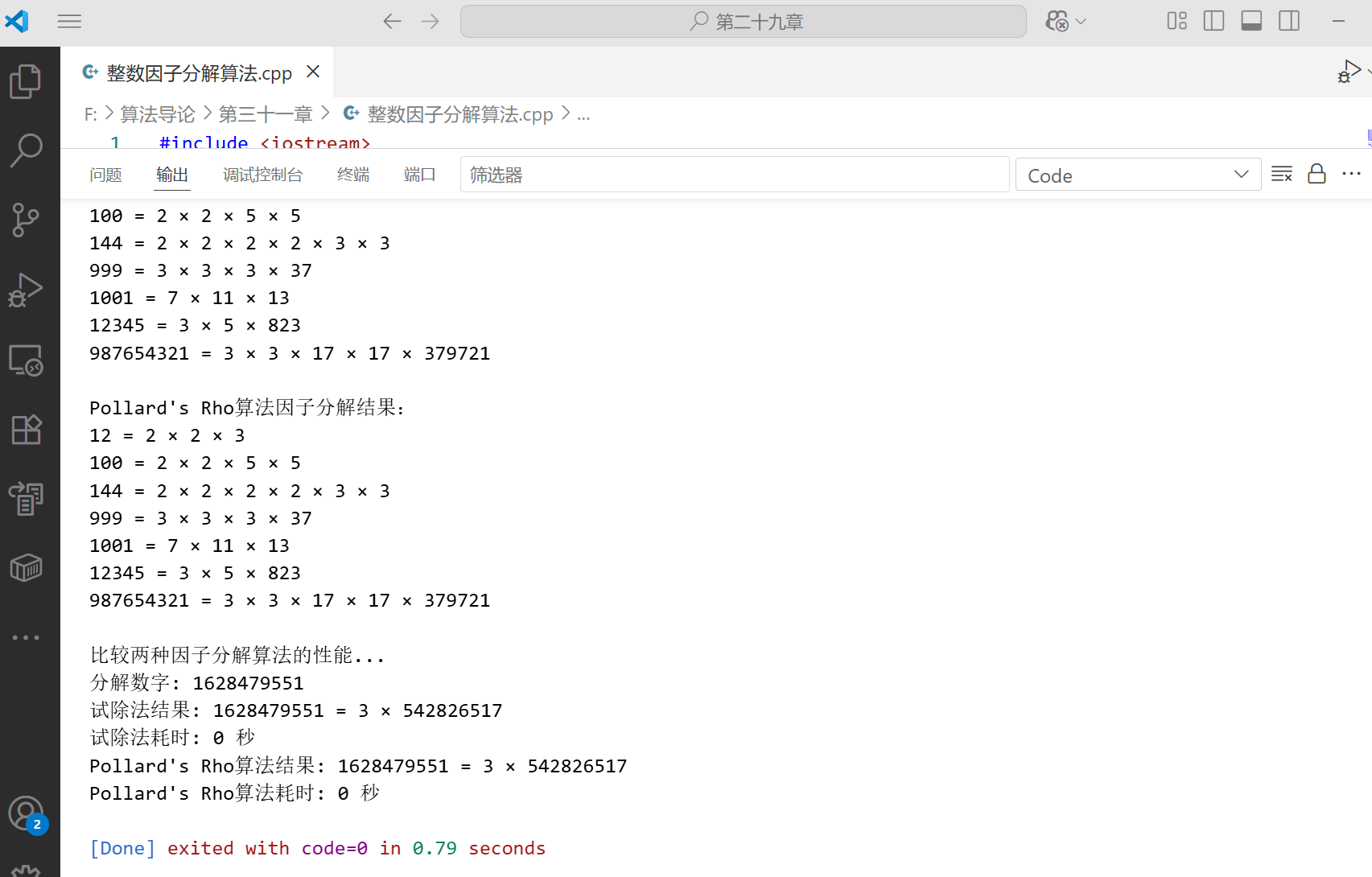
}int main() {// 初始化随机数生成器srand(time(0));// 测试一些数字的因子分解long long numbers[] = {12, 100, 144, 999, 1001, 12345, 987654321};int numCount = sizeof(numbers) / sizeof(numbers[0]);cout << "试除法因子分解结果:" << endl;for (int i = 0; i < numCount; i++) {long long n = numbers[i];vector<long long> factors = trialDivision(n);printFactors(n, factors);}cout << "\nPollard's Rho算法因子分解结果:" << endl;for (int i = 0; i < numCount; i++) {long long n = numbers[i];vector<long long> factors = pollardsRhoFactorization(n);printFactors(n, factors);}// 测试大数字的因子分解long long largeNumber = 1000000007 * 1000000009; // 两个大素数的乘积compareAlgorithms(largeNumber);return 0;
}
代码说明
这段代码实现了两种整数因子分解算法:
trialDivision:试除法分解整数,对于小数字有效,但对于大数字效率很低pollardsRhoFactorization:实现了 Pollard's Rho 算法,这是一种概率性算法,对于大数字的分解效率远高于试除法
代码还包含了一个性能比较函数,展示了 Pollard's Rho 算法在分解大整数时的显著优势。
因子分解是密码学中的一个核心问题,RSA 等加密算法的安全性正是基于大整数因子分解的困难性。虽然 Pollard's Rho 算法比试除法高效得多,但对于足够大的数字(如 2048 位),即使是最先进的因子分解算法也需要极长的时间。
思考题
证明:如果 a 和 b 是正整数,则存在整数 x 和 y 使得 ax + by = gcd (a, b)。
设计一个算法,判断一个数是否为 Carmichael 数(Carmichael 数是合数 n,对于所有与 n 互素的整数 a,都有 a^(n-1) ≡ 1 (mod n))。
实现一个基于中国余数定理的秘密共享方案:将一个秘密分成 k 份,使得需要至少 t 份才能恢复秘密(t ≤ k)。
优化 RSA 算法的实现,使其能够处理更大的数字(如 1024 位或 2048 位),并比较性能差异。
证明:如果 n 是一个奇合数,那么在 [1, n-1] 中至少有一半的数是 n 的 Miller-Rabin 证人(即能证明 n 是合数的数)。
本章注记
第 31 章介绍的数论算法是计算机科学和密码学的基础,这些算法虽然源于古老的数论理论,但在现代信息安全中发挥着至关重要的作用。
欧几里得算法是最古老的算法之一,其历史可以追溯到公元前 300 年左右,但至今仍在广泛使用。扩展欧几里得算法不仅能计算最大公约数,还能求解线性丢番图方程,是模运算和密码学算法的基础。
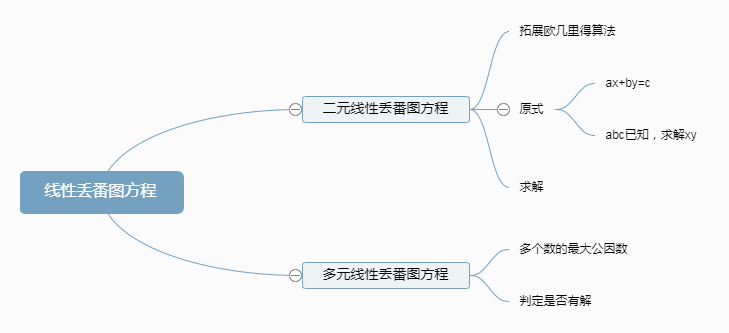
模运算和模线性方程的求解是很多加密算法的核心,而中国余数定理则在提高解密效率方面有重要应用。

RSA 公钥加密系统是第一个实用的公钥加密算法,由 Rivest、Shamir 和 Adleman 于 1977 年提出,其安全性基于大整数因子分解的困难性。尽管已经提出了多种攻击 RSA 的方法,但对于足够大的密钥(如 2048 位或更大),RSA 仍然被认为是安全的。
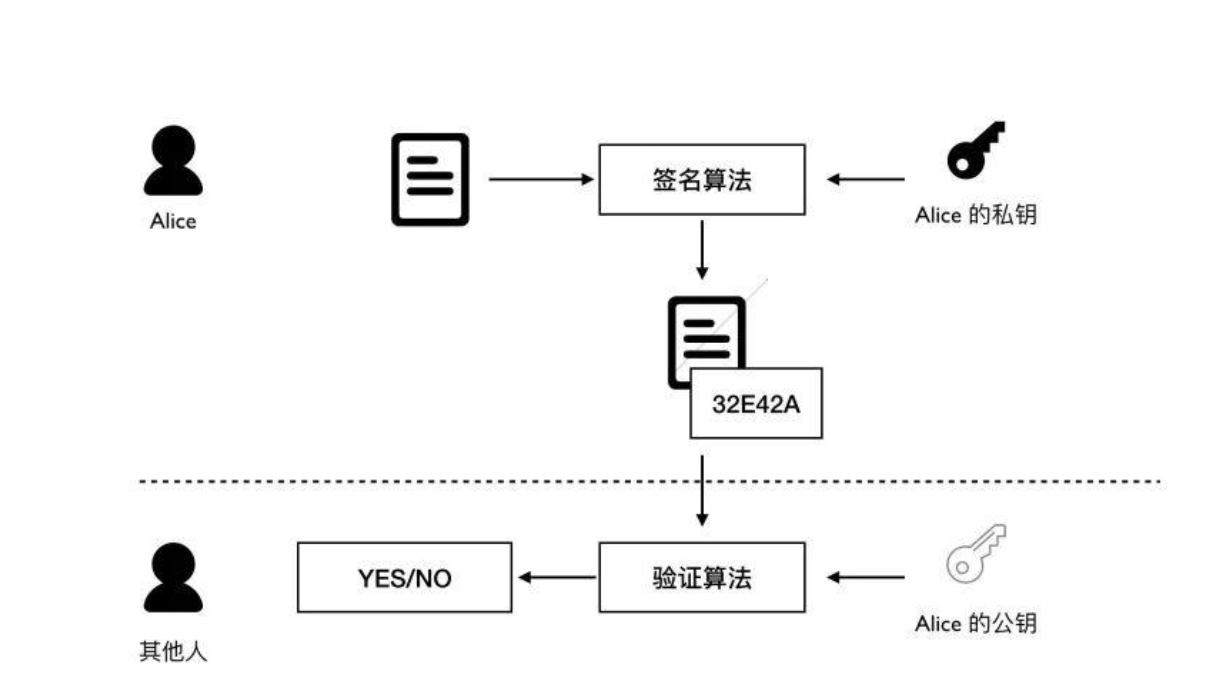
素数测试和整数因子分解是数论中的两个核心问题,也是密码学研究的重点。Miller-Rabin 素数测试和 Pollard's Rho 因子分解算法是这两个领域的代表性算法,在实际应用中有着广泛的用途。

随着量子计算的发展,许多基于数论的加密算法(包括 RSA)可能在未来受到威胁。因此,后量子密码学(Post-Quantum Cryptography)成为了当前研究的热点,旨在开发能够抵抗量子计算攻击的新密码算法。
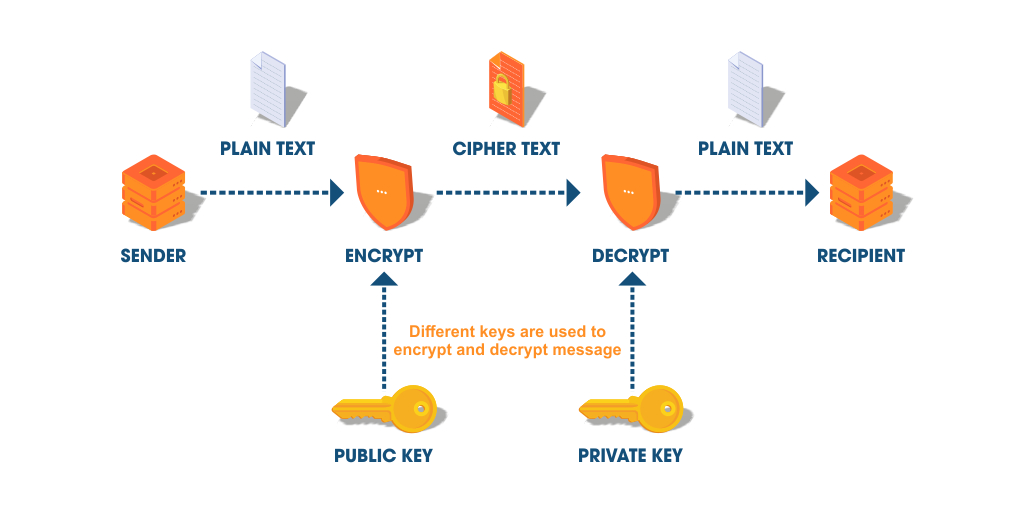
数论算法的研究和应用仍然是一个活跃的领域,新的算法和改进不断涌现,推动着密码学和计算机科学的发展。