当前位置：首页 > web >正文

字符串匹配算法

web 2025/8/16 1:51:44

1 KMP（Knuth-Morris-Pratt）算法原理

1.1 背景介绍
KMP算法是一种高效的字符串匹配算法，由 Donald Knuth、Vaughan Pratt 和 James Morris 于 1977 年独立提出。它通过预处理模式串构建部分匹配表（Partial Match Table, PMT）（或称失败函数 fail 或 lps），在匹配失败时利用该表跳过不必要的比较，从而将时间复杂度优化至线性(O(n+m)。
1.2 核心思想
KMP算法的核心是利用已匹配的信息减少回溯，避免暴力匹配中的重复比较。关键点包括：
部分匹配表（PMT / lps）：记录模式串的最长相同前缀后缀（Longest Prefix Suffix, LPS），用于失配时快速跳转。
匹配过程：在失配时，模式串指针根据 lps 回退，而文本指针不回溯。
1.3 原理
假设如下两个字符串P = “ABCABB”及S = "ABCABCABBE"两个字符串，求P 在S中首次匹配的位置，具体过程如下

先求出P字符的next数组，关于next数组的定义为next[i] 表示P
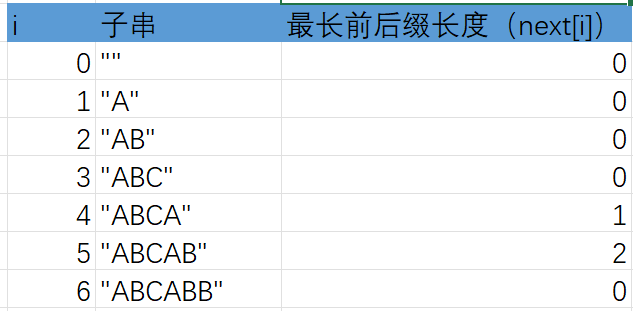
关于next数组的计算除了暴力计算外，还有更好的方法，如下所示：
对于P的前j+1个序列字符：
若p[k] == p[j]，则next[j + 1 ] = next [j] + 1 = k + 1； – 这个大家理解起来都没有问题
若p[k ] ≠ p[j]，如果此时p[ next[k] ] == p[j ]，则next[ j + 1 ] = next[k] + 1，否则继续递归前缀索引k = next[k]，而后重复此过程。–这个理解起来就非常困难了，我们看下面的图：

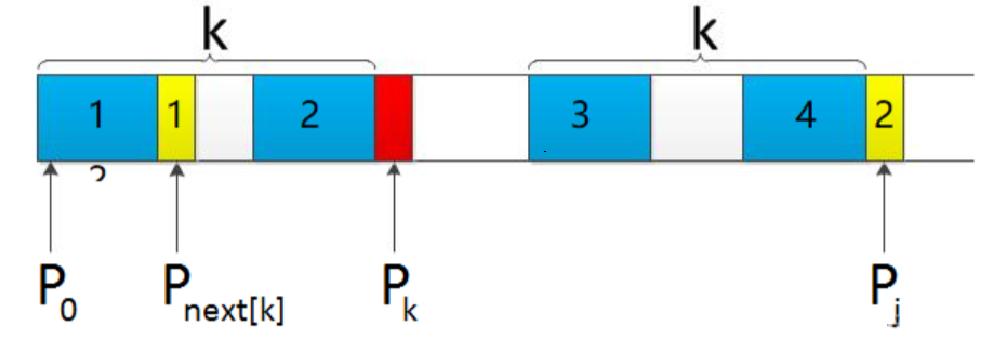
在这里插入图片描述

1、p[k] != p[j]
2、p[0]到p[k-1] 等于 p[j-k]到p[j-1]的，也就是图中最上面K个元素
3、我们现在要找到新的p[0]到p[k’-1] 等于 p[j-k’]到p[j-1]，那么这个新的k怎么求呢？
4、因为p[0]到p[k-1] 等于 p[j-k]到p[j-1]，所以上图中蓝2色块与蓝4色块相等的，现在又要找蓝1色块+黄1色块等于蓝4色块+黄2色块，所以蓝1色块等于蓝2色块，也意味着我们在找p[k]左边的字符串的最长前缀后缀，而这正是next[k]，是不是无巧不成书。

备注：
这里前后缀的定义是不包括字符串本身的，比如子串“AA”的前缀只有两个结果：“”，“A”，"AA"不属于字符串"AA"的前缀，也不属于后缀，字符串“AA”的最长公共前后缀长度为1，故上表中的next[0]与next[1]都是恒等于0的。

字符匹配过程
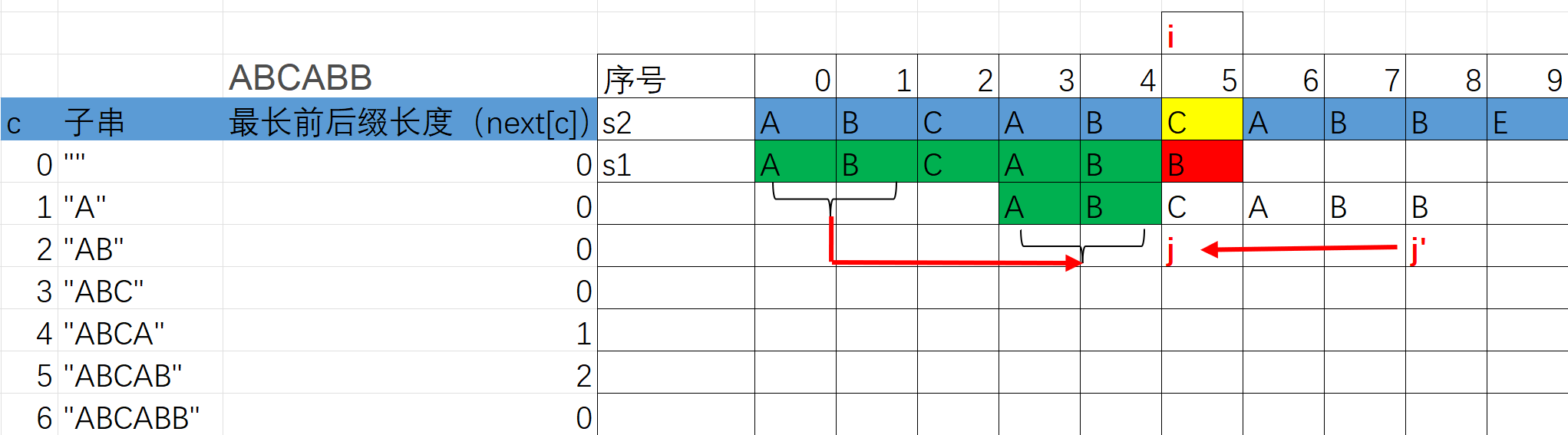
- 初始状态，字符串P与S逐个进行匹配，直到P[5] != S[5]，此时需要将P 往前移动，那移动多少位置呢？可以通过next[5]进行确认，5 为当前P中与S已经匹配的字符个数。next[5] = 2，说明已经匹配的字符串“ABCAB” 最大公共前后缀长度为2，说明可以直接将“ABCAB”往前移动直到前两个字符移动到后面两个字符的位置上去即可，整个匹配的过程i 值不会后退，故整体时间复杂度为O(m + n)