当前位置：首页 > web >正文

【CF】Day125——图论三题

web 2025/8/12 15:22:15

F. 小红的树不动点

题目：

思路：

客串一下牛客

本题让我们求权值之和，那么首先能想到的就是如果 x 有奉献，那么 1 ~ x-1 的数就必须都也出现

什么意思呢？比如下图

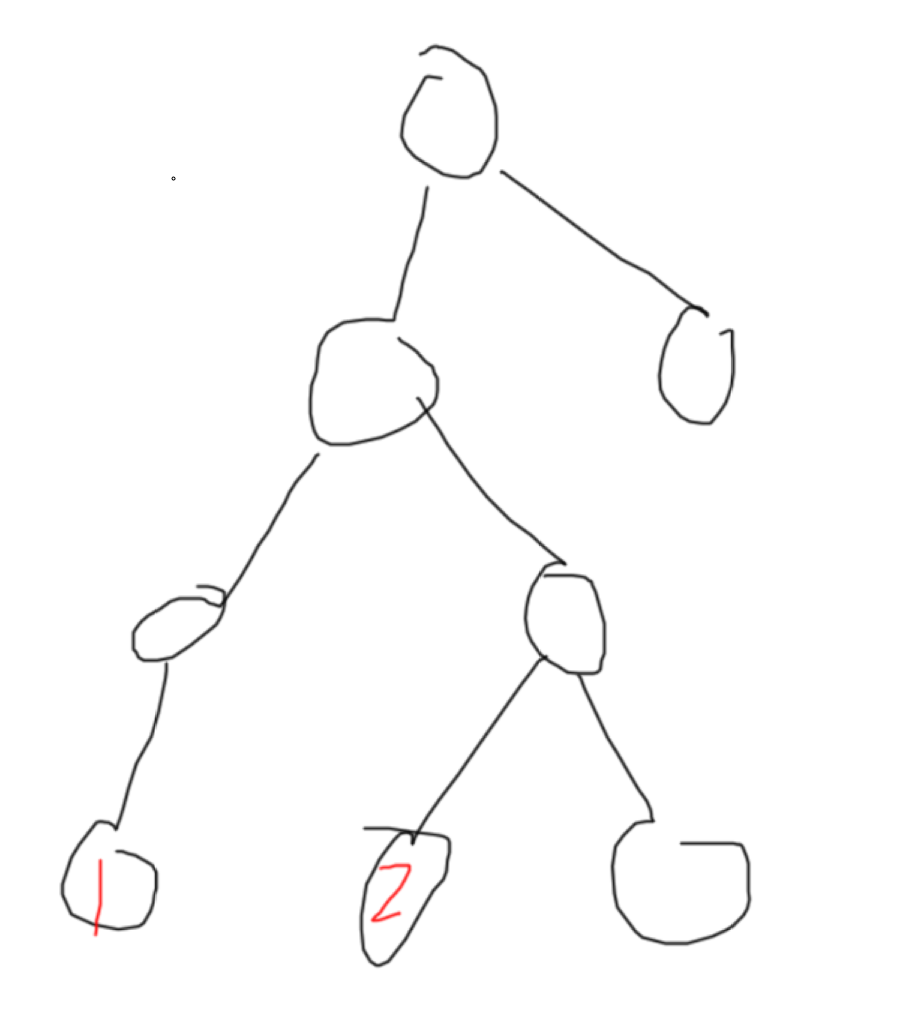
如果 1 造成了奉献，那么显然其奉献大小就是所有其子树中包含 1节点的根的数量，那么都有谁呢？显然就是 1 的所有父节点及其自身，或者说其大小就是 1 的深度，这是显然的

那么对于 2 呢？首先既然 2 要有奉献，那么显然 2 和 1 就要同时出现，那么什么时候会同时出现呢？不难发现就是 1 和 2 的最近公共祖先（LCA）的这个节点能最早同时出现 1 2，所以 2 的奉献就是 1 2 的 LCA 的深度

那么以此类推，3 的奉献就是 1 2 3 LCA 的深度，4 就是 1 2 3 4 的 LCA 的深度...

因此我们只需要从小到大枚举 i 即可，然后看看其 LCA 是谁，然后统计深度即可

这里我们使用dfs序来解决LCA问题，dfn 有一个性质就是其管理的所有节点的 dfn 都满足以下：

dfn[fa] <= dfn[son] <= dfn[fa] + sz[fa] - 1，其中 sz[i] 代表以 i 为根的子树大小

因此我们定义一个全局 lca，初始为 1，然后往后枚举 i，如果 i 的 dfn 不处于 lca 管理的范围内，说明 lca 需要往上跳跃，及 lca = f[lca]，一直到 1 ~ i 均属于 lca 的管理范围内即可

相对于其他 LCA 板子更加简单好写

总结：dfn 是个好东西

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
int n;
vector<vector<int>> g(200005);
int ans = 0;
int tim = 0;
int dep[200005],sz[200005],dfn[200005],f[200005];
void dfs(int fa,int se)
{f[se] = fa;dep[se] = dep[fa]+1;sz[se] = 1;tim++;dfn[se] = tim;for(auto & son : g[se]){if(son == fa) continue;dfs(se,son);sz[se] += sz[son];}
}void solve()
{cin >> n;for (int i = 0; i < n-1; i++){int u,v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}dfs(0,n);int lca = 1;for (int i = 1; i <= n; i++){while (lca > 0 && !(dfn[lca] <= dfn[i] && dfn[lca] + sz[lca] - 1 >= dfn[i])){lca = f[lca];}ans+=dep[lca];}  cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}

C. Tree Pruning

题目：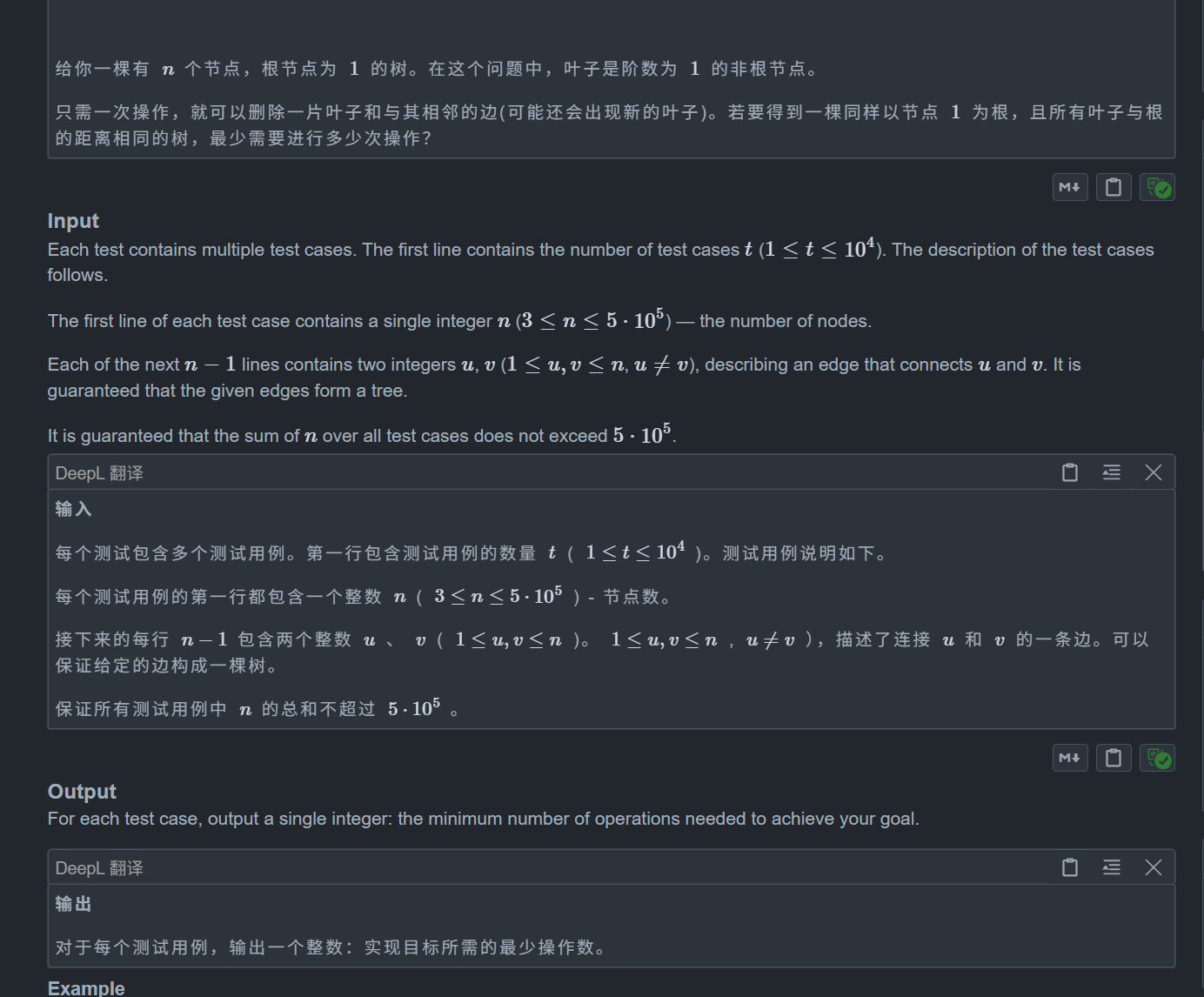

思路：

对前缀和的巧妙运用

题目让我们求进行多少次删除操作才能使得所有叶子节点到根的距离一样，求操作最小数

那么考虑一个问题，什么情况下这个点需要被删除？

①. 这个节点的深度大于我们当前钦定的所需深度 dep

那么显然是要删除的，这是母庸置疑的

②. 这个节点的子树的最大深度小于我们当前钦定的所需深度 dep

此时说明其子树不可能达到 dep，那么这一个节点肯定也不可能满足条件

综上我们只需要找到每个节点的深度，以及每个节点其子树的最大深度即可，然后对二者做一个前缀和即可快速求出，同时二者肯定不会重复计算，因为如果这个节点的深度大于 dep，那么其子树肯定也大于 dep，所以就只满足情况 ①，同时如果最大深度都达不到 dep，那么自身肯定也不是 dep，所以只满足条件 ②

总结：看似简单，实则需要考虑完全

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
//
void solve()
{int n;cin >> n;vector<vector<int>> g(n+1);vector<int> dep(n+1,0),depcnt(n+1,0),mxdep(n+1,0),mxdepcnt(n+1,0);for (int i = 0; i < n-1; i++){int u,v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}auto dfs = [&](auto & self,int fa,int se)->void{//当前节点的深度dep[se] = dep[fa] + 1;//深度 i 的数量depcnt[dep[se]]++;//以该节点为子树的最深的深度mxdep[se] = dep[se];for(auto & son : g[se]){if(son == fa) continue;self(self,se,son);mxdep[se] = max(mxdep[se],mxdep[son]);}//子树内最大深度为 i 的数量mxdepcnt[mxdep[se]]++;};dfs(dfs,1,1);vector<int> sumdepcnt(n+2,0),summxdepcnt(n+2,0);//深度大于 i 的数量for (int i = mxdep[1]; i >= 1; i--){sumdepcnt[i] = sumdepcnt[i+1] + depcnt[i];}//其子树的最大深度小于 i 的数量for (int i = 1; i <= mxdep[1]; i++){summxdepcnt[i] = summxdepcnt[i-1] + mxdepcnt[i];}int ans = 1e9;for (int i = 1; i <= mxdep[1]; i++){//那么要删除的点就是删除所有深度大于 i 的节点和最大深度小于 i 的节点ans = min(ans,sumdepcnt[i+1] + summxdepcnt[i-1]);}    cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

E. Two Chess Pieces

题目：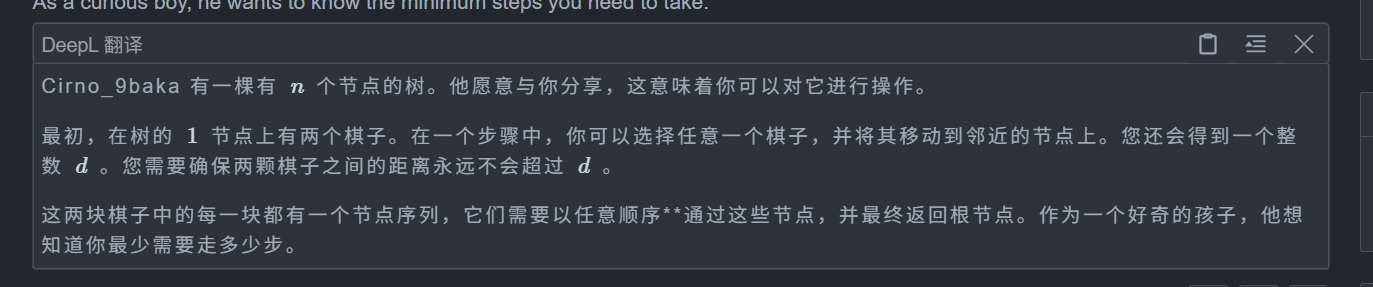

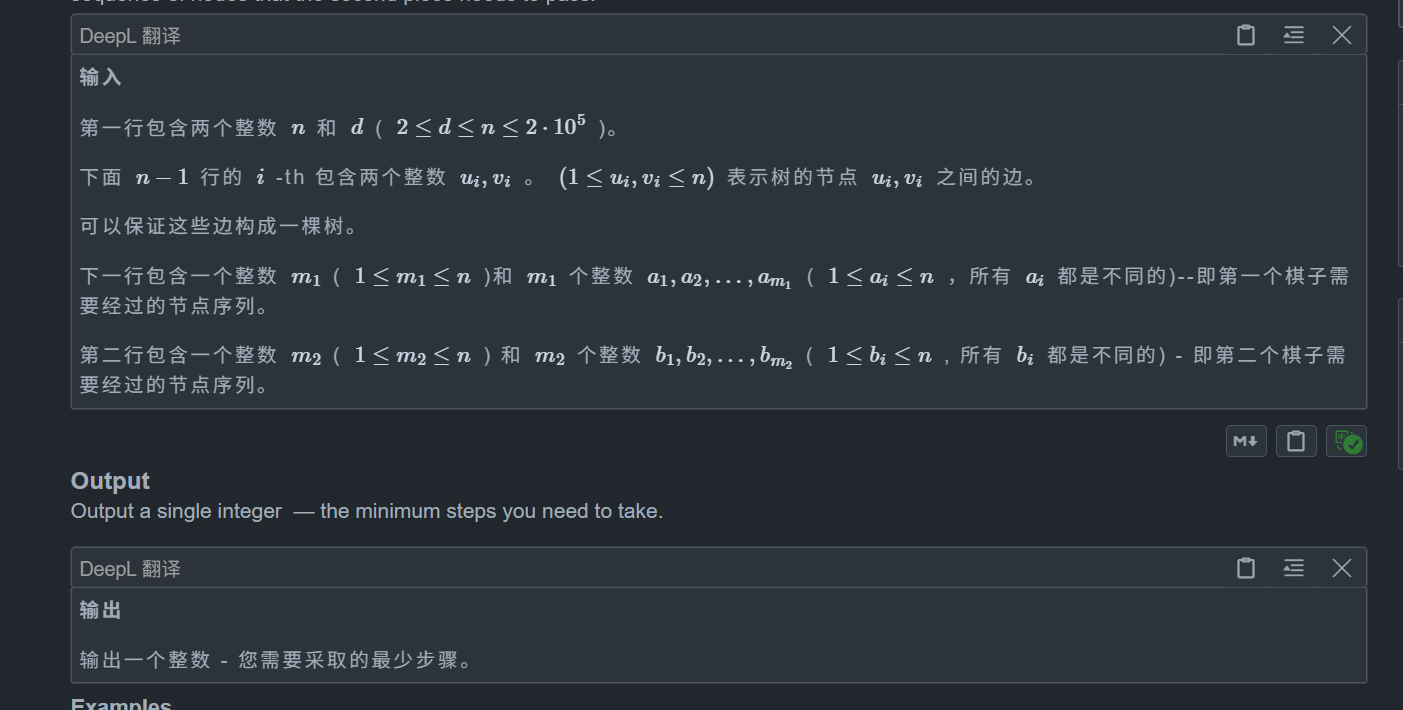思路：

比较经典的一题，之前也做过类似的

题目的条件很简单，就是相当于让我们走完所有的标记点即可，我们先考虑简单情况

假如只有一个节点的限制我们怎么走？我们可以统计每个点的子树内是不是有目标点，如果有的话，那么这个点就必须得走，否则就可以不走

那么就有一个简单版的思路了：初始答案为 2 *（n-1）因为要回到根，如果有一个点是不需要走的，那么就将答案减去 2，因为我们肯定是来回一次这个点

那么现在拓展，现在还要走第二个点，那么怎么判断呢？由于题目中还给了一个约束 d，所以我们还需要考虑第三种情况了

即判断对方节点是不是离自己太远了，那么怎么考虑呢？

我们既然储存了一个子树内的最深节点，那么我们只需要判断一下：如果当前节点不需要走这个节点 u，但是对方在以 u 为根的子树内会走到一个深度为 dep 的点，如果 dep - u >= d，那么说明当前节点肯定要走，不然如果不走这个点就会不满足约束，否则就可以偷懒不走

具体还是一样的做法：初始化答案为 4 * (n-1) 因为有两个点要走，如果找到了上诉说的可以偷懒的点，那么就对答案减 2

实现还是很简单的

总结：思路很重要，正向求难，我们不妨考虑逆向求

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
int n, d;
int musta[200005], mustb[200005];
int mxdepa[200005], mxdepb[200005];
int dep[200005];
int m1, m2;
vector<vector<int>> g(200005);
int ans =0;
void dfs(int fa, int se)
{dep[se] = dep[fa] + 1;if(musta[se]) mxdepa[se] = dep[se];if(mustb[se]) mxdepb[se] = dep[se];    for (auto &son : g[se]){if (son == fa)continue;dfs(se, son);mxdepa[se] = max(mxdepa[se], mxdepa[son]);mxdepb[se] = max(mxdepb[se], mxdepb[son]);}if(!mxdepa[se] && mxdepb[se] - dep[se] < d) ans -=2;if(!mxdepb[se] && mxdepa[se] - dep[se] < d) ans -=2;
}void solve()
{cin >> n >> d;for (int i = 0; i < n - 1; i++){int u, v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}cin >> m1;for (int i = 0; i < m1; i++){int x;cin >> x;musta[x] = 1;}cin >> m2;for (int i = 0; i < m2; i++){int x;cin >> x;mustb[x] = 1;}ans = 4 * (n-1);dfs(0,1);cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}

查看全文

http://www.xdnf.cn/news/17693.html