[LeetCode优选算法专题一双指针——有效三角形的个数]
题目链接
LeetCode有效三角形的个数
题目描述

题目解析
分析 :
首先明确计算规则:从示例 1 可以知道,对于三元组 (2,3,4) 和 (4,3,2),我们只统计了其中的 (2,3,4),并没有把 (4,3,2) 也统计到答案中,所以题目意思是把这两个三元组当成是同一个三元组,我们不能重复统计。
既然有这样的规则,那么不妨规定三角形的三条边 a,b,c 满足:
1 ≤ a ≤ b ≤ c
这可以保证我们在统计合法三元组 (a,b,c) 的个数时,不会把 (c,b,a) 这样的三元组也统计进去。
由于三角形两边之和大于第三边,我们有
- a + b > c
- a + c > b
- b + c > a
上式中的 a + c > b 是必然成立的,因为 a + c ≥ a + b > b(注意 a 至少是 1)。
同样的, b + c > a 也必然成立,因为 b+ c ≥ a+ a = 2 a > a(注意 a 至少是 1)。
所以只需要考虑第一个式子,那么问题变成,从 nums 中选三个数,满足 1 ≤ a ≤ b ≤c 且a + b > c 的方案数。
方法一:枚举最长边 + 相向双指针:
我们可以先给数组里的元素排个序,先固定一个最大的数,然后利用双指针算法结合上面讲的特性来优化算法:
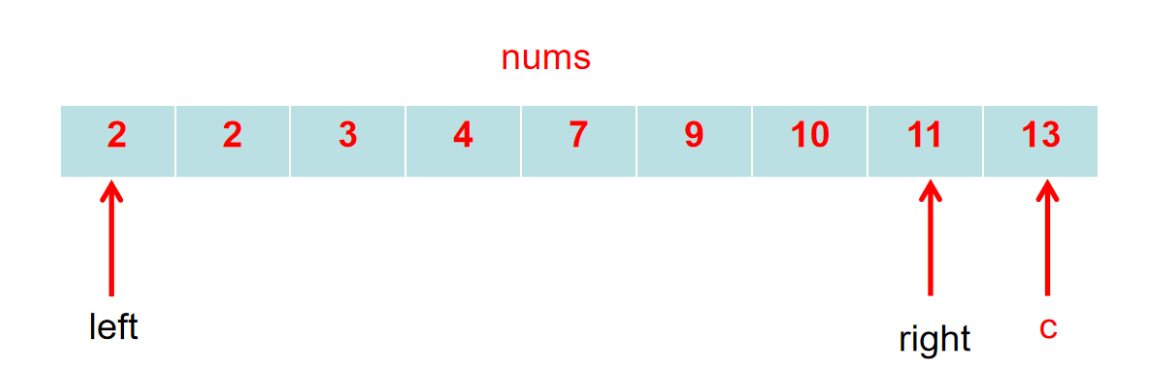
外层循环枚举最长边 c=nums.size(),内层循环用相向双指针枚举 a=nums[left] 和 b=nums[right],具体如下:
初始化左右指针 left=0, right=c−1。
- 情况一:nums[left] + nums[right] > c
- 情况二:nums[left] + nums[right] <= c 小于和等于属于同一种情况,即不能构成三角形
-
单调性基础:数组经过排序后,
nums[left] ≤ nums[right] ≤ nums[i](i为最大边索引) -
情况一:
nums[left] + nums[right] > nums[i]
- 由于数组递增,
nums[left] ≤ nums[left+1] ≤ ... ≤ nums[right-1] - 因此
nums[left+1] + nums[right] > nums[i]、nums[left+2] + nums[right] > nums[i]... 全部成立 - 这意味着
[left, right-1]范围内的所有元素与nums[right]、nums[i]都能组成有效三角形 - 所以直接累加
right - left个有效组合,然后左移right尝试更小的中间边
3.情况二:nums[left] + nums[right] ≤ nums[i]
- 同样由于数组递增,
nums[left] + nums[right-1] ≤ nums[left] + nums[right] - 因此当前
left与任何right' < right组合都无法满足条件 - 必须右移
left来增大两数之和,尝试满足条件
4.外层循环:当一组left和right判断完毕后,左移最大边索引i,重复上述过程
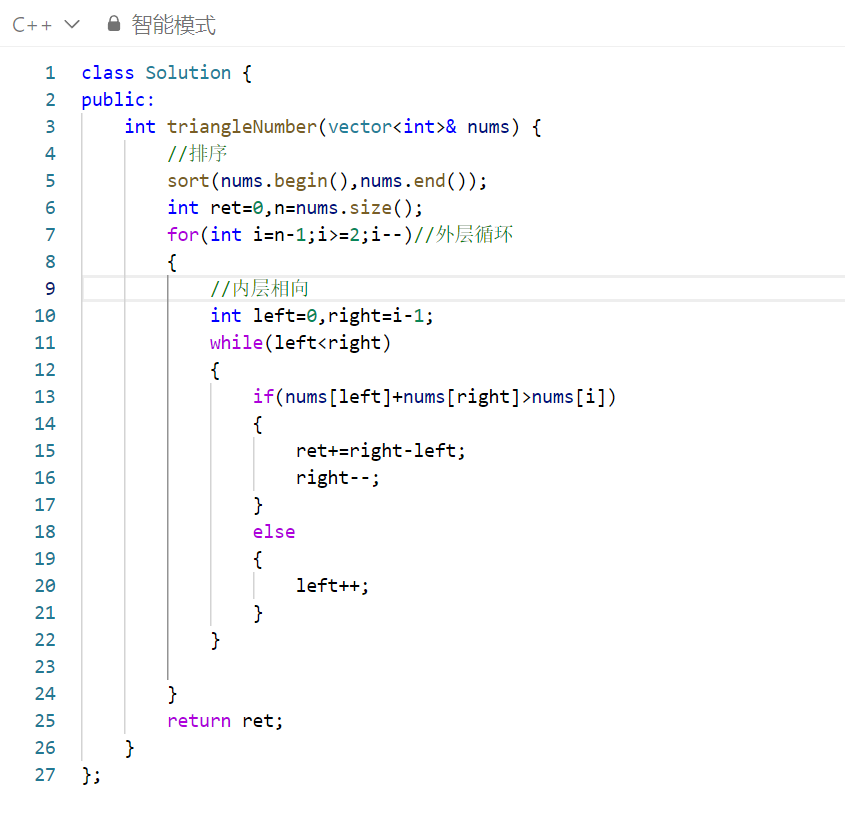
完整代码
复杂度分析
时间复杂度
-
排序阶段:
使用sort函数对数组排序,时间复杂度为 O(n log n),其中n是数组元素个数。 -
双指针遍历阶段:
- 外层循环:从
i = n-1遍历到i = 2,共执行 O(n) 次。 - 内层双指针:对于每个
i,left和right指针在[0, i-1]范围内移动,两者合计移动 O(n) 次(每个元素最多被访问一次)。 - 因此内层循环整体复杂度为 O(n)。
3.总时间复杂度:排序阶段与双指针阶段是串行执行,取量级较大的项,最终为 O(n²)。
空间复杂度
-
排序的空间消耗:
C++ 标准库的sort函数通常采用快速排序(平均情况),空间复杂度为 O(log n)(递归栈开销)。 -
额外变量:
仅使用了ret、n、i、left、right等有限变量,空间消耗为 O(1)。 -
总空间复杂度:
由排序的递归栈主导,因此为 O(log n)。
复杂度对比
- 相比暴力枚举(三重循环,O (n³)),该解法通过排序 + 双指针将时间复杂度从立方级优化到平方级,效率提升显著。
- 空间复杂度保持在对数级,属于高效实现。
这种复杂度特性使得该算法能处理更大规模的输入(如 n = 10^4 级别),而暴力解法在 n = 10^3 时就会出现明显性能瓶颈。
