CSformer：结合通道独立性和混合的稳健多变量时间序列预测

 原文地址：2312.06220

发表会议：AAAI 2025

代码地址:暂无

作者：王浩鑫

团队：四川大学

---

1. 本博客内容主要介绍了此论文到底做了什么？以及我阅读中遇到的一些问题。

2. 因为我本人就是时序预测方向的所以我直接借用AI助手对这篇论文中有疑问的问题进行解读，有可能会有忽略的地方，所以有新问题的朋友欢迎大家在飞书评论区进行讨论而且飞书中也有方法所有关键公式介绍和实验图说明：

Docshttps://h1sy0ntasum.feishu.cn/wiki/L2Kqwb8ssiGSKYkr6KhcImmln3b?from=from_copylink

研究背景与挑战

• 多变量时间序列预测的重要性：在交通管理、电力系统和医疗保健等领域至关重要，但面临时间序列数据中复杂长期依赖关系和变量间相互关系的挑战。

• 现有方法的局限性：基于Transformer的模型在MTSF任务中存在争议，一些研究表明简单的线性模型DLinear在某些情况下表现更优。现有方法要么直接混合信道导致潜在噪声引入，要么采用信道独立方法导致信息丢失。

CSformer模型的核心贡献

• 信道独立与混合的结合：提出了先信道独立后混合的策略，通过两阶段多头自注意力机制，分别提取信道特异性和序列特异性信息，并通过参数共享增强这两种信息的协同效应。

• 维度增强嵌入技术：在嵌入过程中提升序列维度，同时保持原始数据的完整性，为后续的注意力机制处理做好准备。

• 两阶段多头自注意力（MSA）机制：

  • 信道 MSA：在时间步长上应用信道注意力，识别信道间的依赖关系。受到自然语言处理中大规模模型适配的微调技术启发，集成了适配器技术，优化信道信息的提取。

  • 序列 MSA：将信道 MSA的输出重塑后作为序列 MSA的输入，使用与信道 MSA共享的参数，提取序列特征。

• 适配器的应用：在每个MSA机制后加入适配器，确保两个阶段的自注意力机制能够提取不同的特征，增强模型对不同维度信息的识别能力。

模型框架

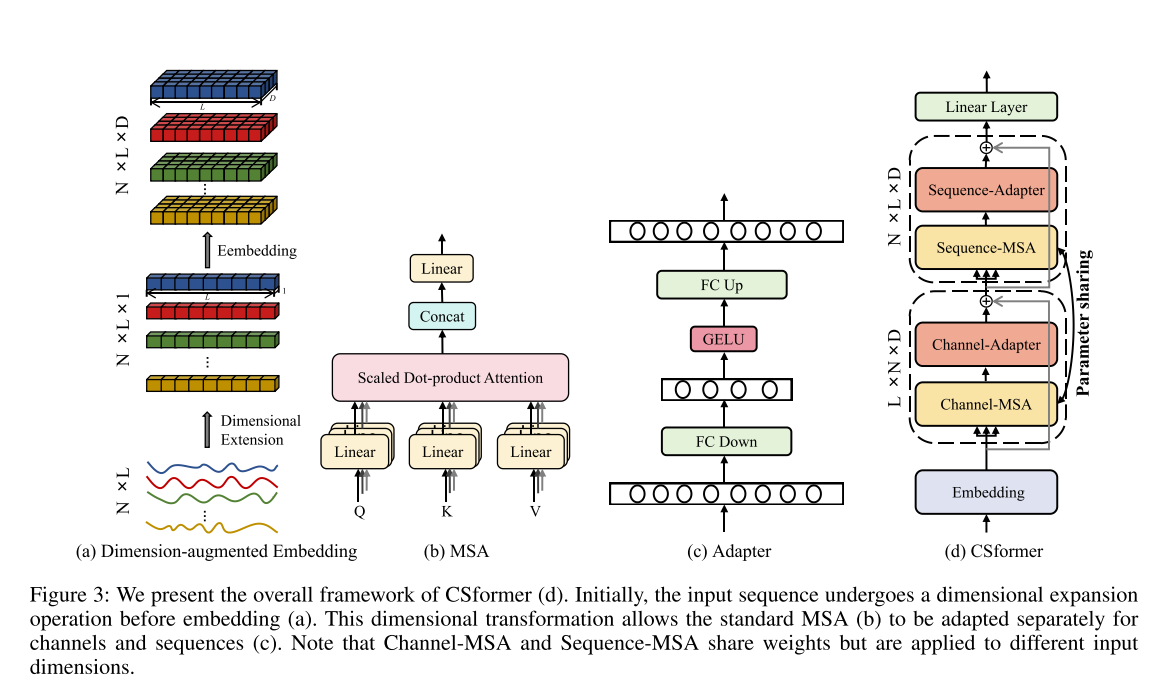
(a) 维度增强嵌入（Dimension-augmented Embedding）

• 输入数据：模型的输入是一个多变量时间序列数据，形状为N×L，其中N是变量（信道）的数量，L是时间序列的长度。

• 维度增强操作：通过将每个时间序列数据扩展到一个新的维度，创建一个形状为N×L×1的三维张量。这一步是为了在不丢失原始信息的情况下增加数据的维度，为后续的嵌入操作做准备。

• 嵌入操作：使用一个可学习的向量ν与增强后的序列进行逐元素相乘，生成嵌入输出H，形状为N×L×D，其中D是嵌入的维度。

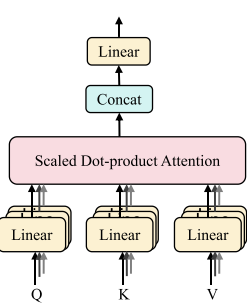
(b) 多头自注意力机制（MSA）

• 输入数据：嵌入后的数据H被输入到MSA模块中。

• 线性变换：对输入数据进行线性变换以生成查询（Q）、键（K）和值（V）矩阵。

• 缩放点积注意力：计算查询和键之间的点积，进行缩放处理后应用Softmax函数得到注意力分数。这些分数用于对值矩阵进行加权求和，生成输出特征。

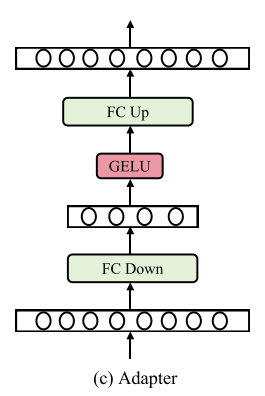
(c) 适配器（Adapter）

• 输入特征：MSA模块的输出被输入到适配器中。

• 下采样和上采样：适配器包含两个全连接层，第一个层将输入特征下采样，第二个层将特征上采样回原始维度。中间使用GELU激活函数以增加模型的非线性表达能力。

• 残差连接：适配器的输出与输入特征进行加法融合，形成残差连接，这有助于缓解梯度消失问题并提高模型的稳定性。

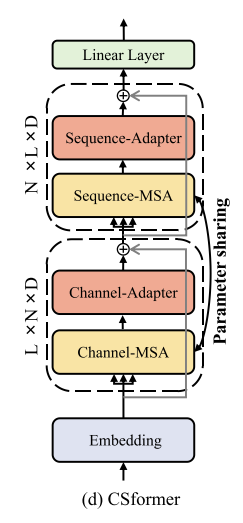
(d) CSformer整体架构

• 嵌入层：输入数据首先经过维度增强嵌入操作，然后进入嵌入层进行特征转换。

• 两阶段MSA和适配器：

  • 信道MSA和信道适配器：首先在信道维度（N）上应用MSA，以捕获变量之间的相互依赖关系，然后通过信道适配器进行特征调整。

  • 序列MSA和序列适配器：接着在序列维度（L）上应用MSA，共享信道MSA的参数，以捕获时间序列中的时间依赖关系，然后通过序列适配器进行特征调整。

• 参数共享：信道MSA和序列MSA共享参数，这种设计增强了不同维度信息之间的交互和融合。

• 输出层：经过两阶段的MSA和适配器处理后，数据被输入到线性层进行最终的预测。

整个CSformer框架通过维度增强嵌入、两阶段的MSA机制和适配器设计，有效地结合了信道独立性和信道混合的优点，提升了多变量时间序列预测的性能。

阅读问题：

可学习的向量ν的向量是什么？他是怎么变化的?

ν的含义和作用

• 维度增强嵌入：ν的作用是将输入数据从形状N×L×1嵌入到高维空间，生成形状为N×L×D的嵌入输出H。通过将原始输入数据与可学习的ν进行逐元素相乘操作，输入数据的每个时间步和每个信道的信息被映射到一个更高维的空间，从而增强了模型对序列和信道信息的表达能力。

• 信息整合：ν的引入使得模型能够学习如何将原始输入数据的不同特征整合到一个更高维的表示中，为后续的多头自注意力机制（MSA）处理做好准备。

ν的变化方式

• 初始化：在模型训练开始之前，ν被随机初始化。通常，它会使用一些标准的初始化方法，如Xavier初始化或Kaiming初始化，以确保初始值在合理的范围内。

• 更新：在模型的训练过程中，ν作为模型的一部分参数，会通过反向传播算法和优化器（如Adam）进行更新。优化器会根据损失函数的梯度信息来调整ν的值，以最小化预测误差。

• 动态调整：随着训练的进行，ν会逐渐学习到如何更好地将输入数据嵌入到高维空间中，以捕捉输入数据中的重要特征和模式。这种动态调整是通过梯度下降法实现的，每次迭代都会根据当前的损失函数值来更新ν的值。