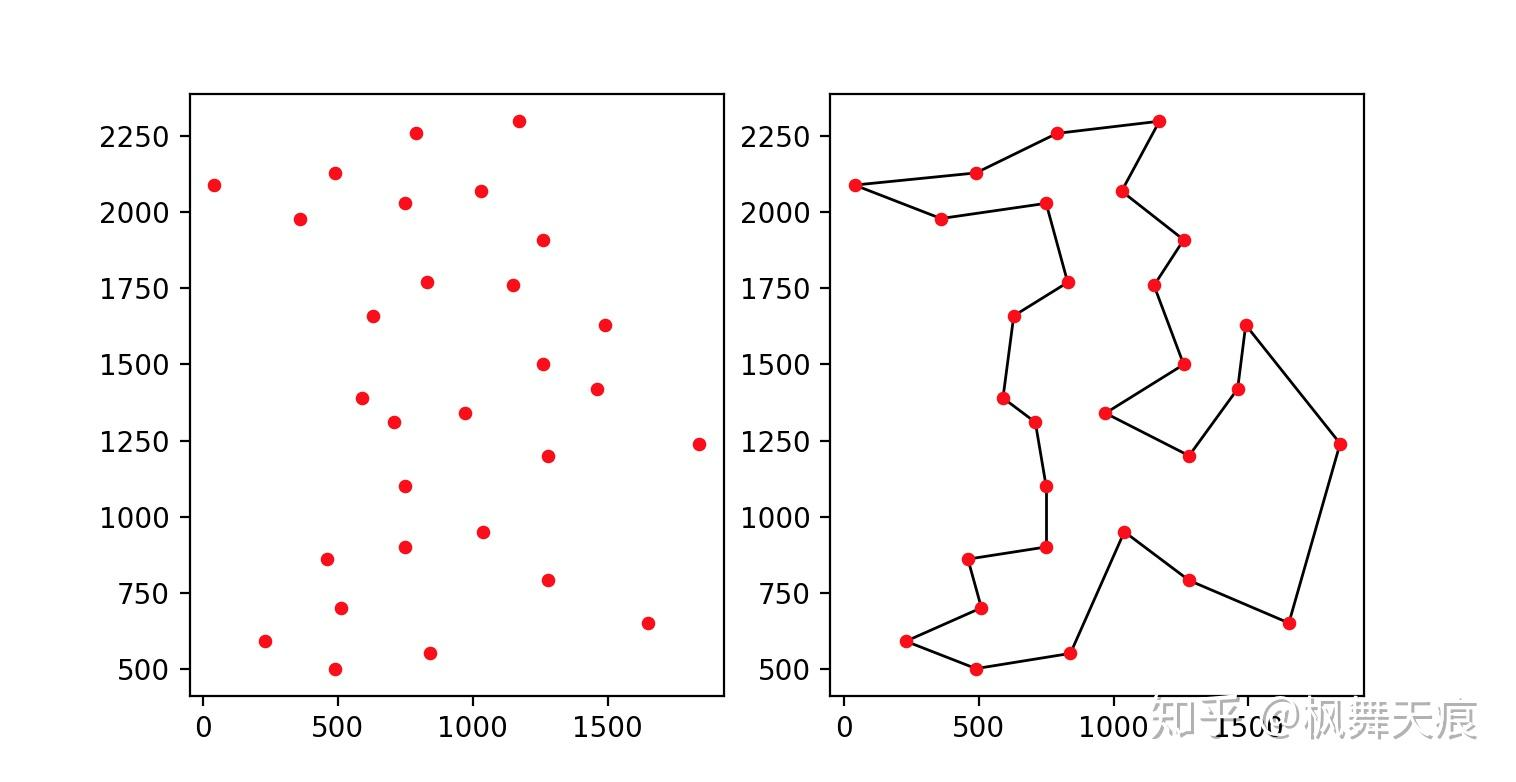
3D曲面上的TSP问题（二）：ACO蚁群算法 + 2-opt搜索求解TSP问题

 由3D曲面上的TSP问题（一）：曲面上点集距离求解-CSDN博客的结果cv::Mat类型的distMap作为输入，使用ACO蚁群算法+2-opt搜索局部优化，解决TSP问题。

#pragma once
#include<iostream>
#include<math.h>
#include<time.h>
#include<opencv2/opencv.hpp>
#include<glm/glm.hpp>
#include <limits>
#include <algorithm>
#include<random>
#include <numeric> // 添加这个头文件using namespace std;class ACO_TSP {
private:cv::Mat distance_matrix;      // 距离矩阵int num_cities;          // 城市数量int num_ants;            // 蚂蚁数量int max_iter;            // 最大迭代次数double alpha;            // 信息素重要程度double beta;             // 启发信息重要程度double rho;              // 信息素挥发系数double q0;               // 探索概率double tau0;             // 初始信息素cv::Mat pheromone;           // 信息素矩阵cv::Mat heuristic;           // 启发信息矩阵(1/distance)vector<vector<int>> ant_paths;       // 蚂蚁路径vector<double> ant_path_lengths;    // 蚂蚁路径长度vector<int> best_path;              // 全局最优路径double best_length;                 // 全局最优路径长度// 蚂蚁构建路径void construct_ant_paths() {// 使用全局随机设备生成一个种子std::random_device rd;unsigned int global_seed = rd();#pragma omp parallel{int thread_id = omp_get_thread_num();unsigned int local_seed = global_seed + thread_id + std::hash<std::thread::id>{}(std::this_thread::get_id());thread_local std::mt19937_64 gen(local_seed);thread_local std::uniform_int_distribution<int> dist(0, num_cities - 1);thread_local std::uniform_real_distribution<double> prob_dist(0.0, 1.0);#pragma omp forfor (int k = 0; k < num_ants; ++k){vector<bool> visited(num_cities, false);cv::Mat probability = cv::Mat::zeros(num_cities, num_cities, CV_64F);// 每只蚂蚁随机选择起点城市int start_city = dist(gen);ant_paths[k][0] = start_city;visited[start_city] = true;// 构建完整路径for (int i = 1; i < num_cities; ++i) {int current_city = ant_paths[k][i - 1];// 计算转移概率
double sum = 0.0;
for (int j = 0; j < num_cities; ++j) {if (!visited[j]) {probability.at<double>(current_city, j) =pow(pheromone.at<double>(current_city, j), alpha) *pow(heuristic.at<double>(current_city, j), beta);sum += probability.at<double>(current_city, j);}else {probability.at<double>(current_city, j) = 0.0;}
}// 选择下一个城市
double q = prob_dist(gen);int next_city = -1;
if (q <= q0) {// 选择概率最大的城市double max_prob = 0.0;for (int j = 0; j < num_cities; ++j) {if (!visited[j] && probability.at<double>(current_city, j) > max_prob) {max_prob = probability.at<double>(current_city, j);next_city = j;}}
}
else {// 轮盘赌选择if (sum > 0) {double threshold = prob_dist(gen) * sum;double accum = 0.0;for (int j = 0; j < num_cities; ++j) {if (!visited[j]) {accum += probability.at<double>(current_city, j);if (accum >= threshold) {next_city = j;break;}}}}}// 如果所有城市都已访问(理论上不应该发生)if (next_city == -1) {for (int j = 0; j < num_cities; ++j) {if (!visited[j]) {next_city = j;break;}}}ant_paths[k][i] = next_city;visited[next_city] = true;}// 计算路径长度ant_path_lengths[k] = calculate_path_length(ant_paths[k]);}}
}// 计算路径长度
double calculate_path_length(const vector<int>& path) {double length = 0.0;for (int i = 0; i < num_cities - 1; ++i) {length += distance_matrix.at<double>(path[i], path[i + 1]);}return length;
}// 更新信息素
void update_pheromone() {// 信息素挥发pheromone *= (1.0 - rho);// 限制信息素最小值double min_pher = tau0 / 10.0;for (int i = 0; i < num_cities; ++i) {for (int j = 0; j < num_cities; ++j) {if (pheromone.at<double>(i, j) < min_pher) {pheromone.at<double>(i, j) = min_pher;}}}// 蚂蚁释放信息素for (int k = 0; k < num_ants; ++k) {double delta_tau = 1.0 / ant_path_lengths[k];for (int i = 0; i < num_cities - 1; ++i) {int city1 = ant_paths[k][i];int city2 = ant_paths[k][i + 1];pheromone.at<double>(city1, city2) += delta_tau;pheromone.at<double>(city2, city1) += delta_tau;}// 闭合路径int last_city = ant_paths[k].back();int first_city = ant_paths[k][0];pheromone.at<double>(last_city, first_city) += delta_tau;pheromone.at<double>(first_city, last_city) += delta_tau;}
}// 修改后的2-opt应用策略
void apply_local_search(int iter) {random_device rd;mt19937 gen(rd());// 1. 只对前20%的优秀蚂蚁进行局部搜索int elite_num =  max(1, num_ants / 5);// 创建索引并根据路径长度排序vector<size_t> indices(num_ants);std::iota(indices.begin(), indices.end(), 0);sort(indices.begin(), indices.end(), [this](size_t a, size_t b) {return ant_path_lengths[a] < ant_path_lengths[b];});// 2. 概率性决定是否进行2-optdouble local_search_prob = std::min(0.8, 0.5 + 0.3 * (double(iter) / max_iter));uniform_real_distribution<double> prob_dist(0.0, 1.0);for (int i = 0; i < elite_num; ++i) {int k = indices[i];// 3. 优质路径有更高概率接受优化if (prob_dist(gen) < local_search_prob) {if (iter >= 3) // 从第3次开始才开始进行2-opt{// 4. 限制2-opt的搜索深度fast_two_opt(ant_paths[k], 200); // 最多尝试10次改进}ant_path_lengths[k] = calculate_path_length(ant_paths[k]);}// 更新全局最优if (ant_path_lengths[k] < best_length) {best_length = ant_path_lengths[k];best_path = ant_paths[k];}}
}void fast_two_opt(vector<int>& path, int max_improvements) {bool improved = true;int improvements = 0;random_device rd;mt19937 gen(rd());while (improved && improvements < max_improvements) {improved = false;// 使用更安全的随机数生成方式uniform_int_distribution<int> i_dist(0, num_cities - 2);uniform_int_distribution<int> j_dist(0, num_cities - 1);int i_start = i_dist(gen);int j_start = j_dist(gen);// 使用双重循环但限制迭代次数int max_tries = num_cities * num_cities; // 防止无限循环int tries = 0;for (int i = i_start; tries < max_tries && !improved; i = (i + 1) % (num_cities - 1)) {for (int j = (i == i_start) ? j_start : 0;j < num_cities && !improved && tries < max_tries;j = (j + 1) % num_cities) {tries++;if (abs(i - j) < 2) continue;int a = path[i];int b = path[i + 1];int c = path[j];int d = path[(j + 1) % num_cities];double current = distance_matrix.at<double>(a, b) + distance_matrix.at<double>(c, d);double proposed = distance_matrix.at<double>(a, c) + distance_matrix.at<double>(b, d);if (proposed < current) {if (i < j) {reverse(path.begin() + i + 1, path.begin() + j + 1);}else {reverse(path.begin() + j + 1, path.begin() + i + 1);}improved = true;improvements++;}}}}}public:ACO_TSP(const cv::Mat& dist_mat, int max_iterations = 100): distance_matrix(dist_mat.clone()), max_iter(max_iterations) {num_cities = distance_matrix.rows;init_parameters();}// 初始化参数
void init_parameters() {num_ants = num_cities * 50;alpha = 1.0;beta = 2.0;rho = 0.5;q0 = 0.75;// 计算最近邻距离作为初始信息素参考double nn_dist = 0.0;for (int i = 0; i < num_cities; ++i) {double min_dist = INFINITY;for (int j = 0; j < num_cities; ++j) {if (i != j && distance_matrix.at<double>(i, j) < min_dist) {min_dist = distance_matrix.at<double>(i, j);}}nn_dist += min_dist;}tau0 = 1.0 / (num_cities * nn_dist / num_cities);// 初始化信息素矩阵pheromone = cv::Mat::ones(num_cities, num_cities, CV_64F) * tau0;// 初始化启发信息矩阵heuristic = cv::Mat::zeros(num_cities, num_cities, CV_64F);for (int i = 0; i < num_cities; ++i) {for (int j = 0; j < num_cities; ++j) {if (i != j) {heuristic.at<double>(i, j) = 1.0 / distance_matrix.at<double>(i, j);}}}ant_paths.resize(num_ants, vector<int>(num_cities));ant_path_lengths.resize(num_ants);best_length = INFINITY;
}bool solve() {for (int iter = 0; iter < max_iter; ++iter) {construct_ant_paths();// 替换原来的全量2-opt为选择性优化apply_local_search(iter);update_pheromone();// 动态调整参数rho = max(0.1, 0.5 * (1.0 - double(iter) / max_iter));q0 = min(0.95, 0.7 + 0.25 * (double(iter) / max_iter));cout << "Iteration " << iter << ", Best length: " << best_length << endl;}return true;}vector<int> get_best_path() const { return best_path; }double get_best_length() const { return best_length; }
};