310. 最小高度树

题目

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，任何一个没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

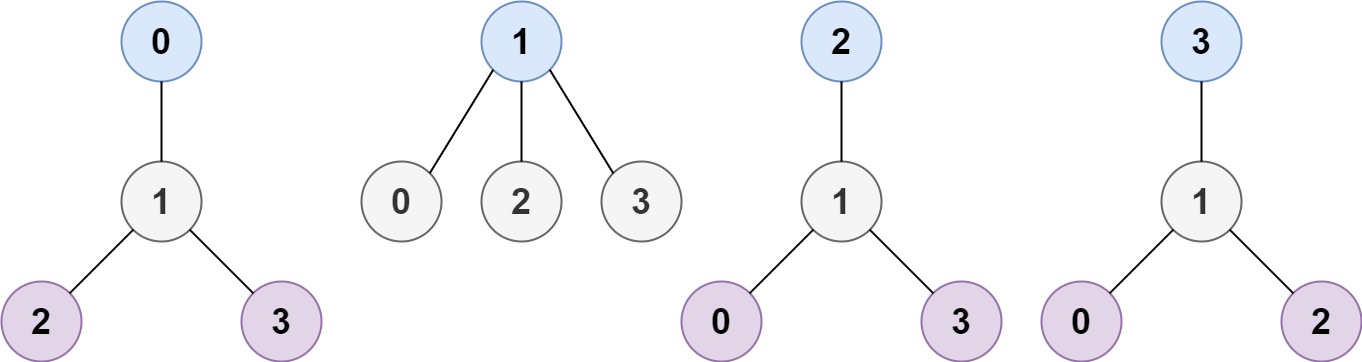
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

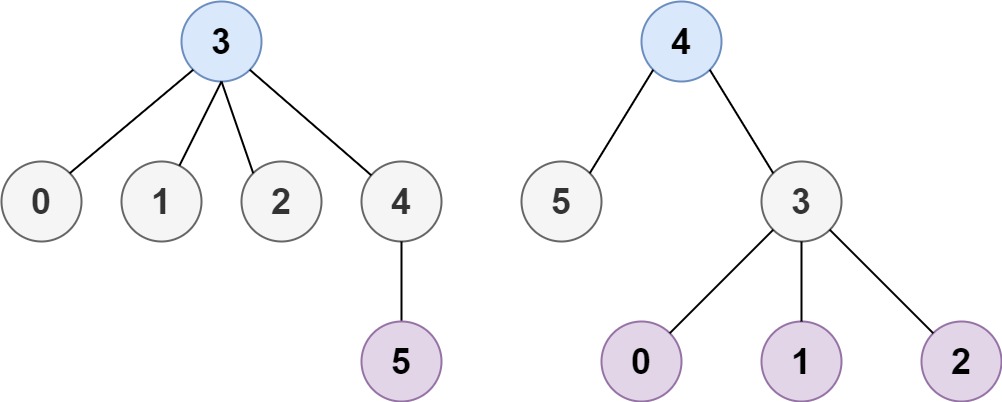
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• 所有 (ai, bi) 互不相同
• 给定的输入 保证 是一棵树，并且 不会有重复的边

思路

        我们可以通过树的直径特性来寻找最小高度树的根节点。我们可以先找到树中两个最远节点之间的路径，通过dfs可以确定树的直径,先从任意节点出发找到最远节点x，再从x出发找到最远节点y，路径x-y就是树的直径，然后通过回溯路径找到直径的中心节点，如果直径长度为奇数，中心为中间一个节点，如果为偶数，中心为中间两个节点。

代码

class Solution {
public://更新所有节点到u的距离dist和父节点parentvoid dfs(int u, vector<int> & dist, vector<int> & parent, const     vector<vector<int>> & a) {for (size_t i=0;i<a[u].size();i++){int v=a[u][i];if (dist[v]<0)//邻居v未被访问{dist[v]=dist[u]+1;//更新距离parent[v]=u;//记录父节点dfs(v,dist,parent,a);//递归访问v}}}//从节点u出发,找到距离u最远的节点,并返回该节点的编号int ll(int u,vector<int> &parent,const vector<vector<int>> &a){int n=a.size();vector<int> dist(n,-1);dist[u]=0;dfs(u,dist,parent,a);//更新距离和父节点int maxdist=0;int node=-1;for (int i=0;i<n;i++){if(dist[i]>maxdist){maxdist=dist[i];node=i;}}return node;}vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {if (n==1){return {0};}vector<vector<int>> a(n);//存每个节点的邻居for (auto &edge:edges){a[edge[0]].emplace_back(edge[1]);a[edge[1]].emplace_back(edge[0]);}vector<int> parent(n, -1);//找到距离节点0最远的节点xint x=ll(0,parent,a);//找到距离节点x最远的节点yint y=ll(x,parent,a);//找到节点x到节点y的路径vector<int> path;parent[x]=-1;while(y!=-1)//从节点y开始,沿着parent数组回溯到x，得到路径path{path.emplace_back(y);//存储的是从y到x的路径y=parent[y];}int m=path.size();if (m%2==0)//两个节点{return {path[m/2-1],path[m/2]};}else//一个节点{return {path[m/2]};}}
};