当前位置：首页 > ops >正文

代码随想录第37天：动态规划10（公共子序列问题）

ops 2025/9/4 11:13:51

一、不相交的线（Leetcode 1035）

给定两个整数数组 nums1 和 nums2，我们可以在两个数组中画线，连接两个相等的数字，但：

线不能交叉。
每个元素最多使用一次。

目标：返回可以连接的最大连线数。

本质：找两个数组的最长公共子序列。

1.dp数组定义：

dp[i][j] 表示 nums1[0..i-1] 和 nums2[0..j-1] 的最长公共子序列长度。

2.状态转移：

if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1
else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])

3.dp数组初始化：

dp = [[0] * (n + 1) for _ in range(m + 1)]

class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:m, n = len(nums1), len(nums2)dp = [[0] * (n + 1) for _ in range(m + 1)]for i in range(1, m + 1):for j in range(1, n + 1):if nums1[i - 1] == nums2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[m][n]

二、最大子序和（Leetcode 53）

题意：给定一个整数数组 nums，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

1.dp数组定义：

dp[i]：以第 i 个元素结尾的连续子数组的最大和

2.状态转移方程：

要么单独成为新的子数组（nums[i]）
要么延续前面的最大子数组（dp[i-1] + nums[i]）

最终答案是所有 dp[i] 中的最大值。

dp[i] = max(nums[i], dp[i-1] + nums[i])

class Solution:def maxSubArray(self, nums: List[int]) -> int:# dp[i] 表示以第 i 个元素结尾的最大子数组和dp = [0] * len(nums)dp[0] = nums[0]  # 初始化第一个元素max_sum = nums[0]  # 初始化最大子数组和for i in range(1, len(nums)):# 状态转移：当前值要么单独成段，要么加到前面段里dp[i] = max(nums[i], dp[i - 1] + nums[i])max_sum = max(max_sum, dp[i])  # 更新最大值return max_sum  # 返回全局最大子数组和

Kadane 算法（空间优化版）

class Solution:def maxSubArray(self, nums: List[int]) -> int:# cur_sum 表示以当前位置结尾的子数组最大和# max_sum 表示所有子数组中出现过的最大和cur_sum = max_sum = nums[0]  # 初始化为第一个元素for num in nums[1:]:# 要么从当前元素重新开始，要么继续累加之前的和cur_sum = max(num, cur_sum + num)max_sum = max(max_sum, cur_sum)  # 更新全局最大值return max_sum  # 返回最大子数组和

三、判断子序列（Leetcode 392）

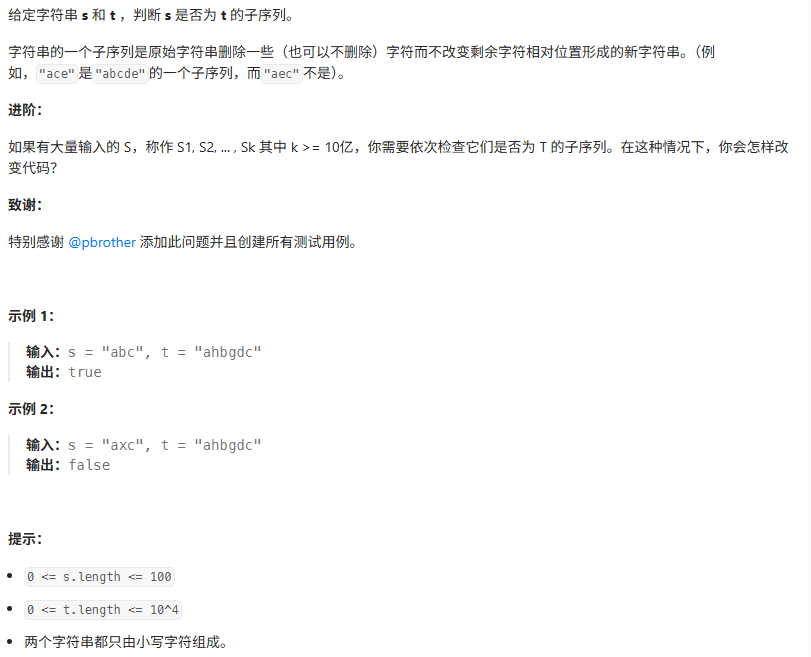
动态规划：

1.dp数组定义：

dp[i][j] 表示 s[0:i] 和 t[0:j] 的最长公共子序列长度。

如果最终的 dp[len(s)][len(t)] == len(s)，说明 s 是 t 的子序列

2.状态转移方程

如果两个字符相等，我们可以将它们纳入公共子序列。
否则，我们选择跳过 s[i-1] 或 t[j-1] 中的一个，取较大的结果。

if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1
else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])

class Solution:def isSubsequence(self, s: str, t: str) -> bool:m, n = len(s), len(t)# 初始化 DP 数组，大小为 (m+1) x (n+1)，初始值为 0dp = [[0] * (n + 1) for _ in range(m + 1)]# 填表：动态规划求 LCSfor i in range(1, m + 1):for j in range(1, n + 1):if s[i - 1] == t[j - 1]:# 字符匹配，公共子序列 +1dp[i][j] = dp[i - 1][j - 1] + 1else:# 不匹配，取之前的最大值dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])# 如果 s 是 t 的子序列，公共子序列长度应等于 len(s)return dp[m][n] == m

双指针法（易于理解）

指针 i 遍历字符串 s，指针 j 遍历字符串 t。
每次匹配成功一个字符，i 向后移动。
最后判断是否 i == len(s)，表示 s 的所有字符都按顺序在 t 中出现。

class Solution:def isSubsequence(self, s: str, t: str) -> bool:i, j = 0, 0  # i 指向 s，j 指向 twhile i < len(s) and j < len(t):if s[i] == t[j]:i += 1  # 如果匹配，移动 s 的指针j += 1      # t 总是要向后遍历return i == len(s)  # 如果 s 全部匹配完，则是子序列

进阶：

如果我们有：

一个很长的字符串 t
成千上万的字符串 s1, s2, ..., sn，需要判断它们是否是 t 的子序列

那么我们不能每次都从头扫描 t，那样会非常慢（总时间复杂度是 O(m × n)）。

from bisect import bisect_right
from collections import defaultdictclass SubsequenceChecker:def __init__(self, t: str):# 预处理 t，将每个字符的出现位置用列表存起来# 例如 t = "abcab" -> {'a': [0, 3], 'b': [1, 4], 'c': [2]}self.index_map = defaultdict(list)for i, ch in enumerate(t):self.index_map[ch].append(i)def isSubsequence(self, s: str) -> bool:pos = -1  # 初始化上一个匹配字符在 t 中的位置，起始为 -1for ch in s:# 在 t 中查找字符 ch 出现的位置中，找到第一个 > pos 的下标（用二分查找）idx = bisect_right(self.index_map[ch], pos)# 如果没有找到合法的位置（idx 越界），说明 s 不是 t 的子序列if idx == len(self.index_map[ch]):return False# 找到了下一个匹配字符的位置，更新 pos 以备下次查找pos = self.index_map[ch][idx]# 所有字符都顺序匹配成功，说明 s 是 t 的子序列return True

小结：
如果只判断是否为子序列，双指针是最快的（O(m + n)）。
若要处理多个 s 查一个 t，推荐预处理 + 二分。
如果要支持更复杂变体（如出现次数、最长长度、删除次数），用 DP，并考虑空间优化。

四、不同的子序列（Leetcode 115）

1.dp数组定义：

dp[i][j] 表示 s[0:i-1] 中子序列等于 t[0:j-1] 的个数。

2.状态转移方程

dp[i-1][j-1]：使用当前字符 s[i-1] 和 t[j-1] 匹配
dp[i-1][j]：跳过 s[i-1]，继续找机会匹配 t[j]

if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
else:dp[i][j] = dp[i-1][j]

3.dp数组初始化：

dp[0][0] = 1  # 空字符串匹配空字符串# dp[i][0] = 1: 任何 s[0:i] 对空字符串 t 都只有一个子序列 ""（删光）
# dp[0][j>0] = 0: 空字符串 s 无法组成任何非空 t

class Solution:def numDistinct(self, s: str, t: str) -> int:m, n = len(s), len(t)# 定义二维 dp 表，dp[i][j] 表示 s 的前 i-1 个字符中子序列等于 t 的前 j-1个字符的个数dp = [[0] * (n + 1) for _ in range(m + 1)]# 初始化：任何字符串匹配空字符串 t 都有 1 种方案（删除所有字符）for i in range(m + 1):dp[i][0] = 1# 填表for i in range(1, m + 1):for j in range(1, n + 1):if s[i - 1] == t[j - 1]:# 两种情况：# 1. 匹配当前字符：使用 s[i-1] 来匹配 t[j-1]，对应 dp[i-1][j-1]# 2. 不匹配当前字符：跳过 s[i-1]，对应 dp[i-1][j]dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]else:# 字符不相同，只能跳过 s[i-1]dp[i][j] = dp[i - 1][j]# 返回最终结果：s 的全部字符匹配 t 的全部字符的方案数return dp[m][n]

一维数组：

class Solution:def numDistinct(self, s: str, t: str) -> int:m, n = len(s), len(t)# 定义一维 dp 数组，dp[j] 表示 s 的前 i 个字符匹配 t 的前 j 个字符的个数dp = [0] * (n + 1)dp[0] = 1  # 空字符串 t 永远是任何 s 的子序列，有 1 种匹配方式# 遍历 s 的每个字符（从 1 到 m）for i in range(1, m + 1):# 由于当前 dp[j] 依赖的是上一轮的 dp[j-1]，为了不被覆盖，# 需要从右向左更新（逆序）for j in range(n, 0, -1):if s[i - 1] == t[j - 1]:# 当前字符匹配成功，dp[j] 累加上一状态 dp[j - 1]dp[j] += dp[j - 1]# 返回匹配完整 t 所有字符的方案数return dp[n]

五、两个字符串的删除操作（Leetcode 583.）

1.dp数组定义：

dp[i][j] 表示 word1[0:i] 与 word2[0:j] 的最长公共子序列长度

2.状态转移：

如果我们知道 word1 和 word2 的最长公共子序列长度为 lcs_len，
那么：

从 word1 删除 len(word1) - lcs_len 个字符
从 word2 删除 len(word2) - lcs_len 个字符
最后返回 len(word1) + len(word2) - 2 * lcs_len

(len(word1) - lcs_len) + (len(word2) - lcs_len) = len(word1) + len(word2) - 2 * lcs_len

class Solution:def minDistance(self, word1: str, word2: str) -> int:m, n = len(word1), len(word2)# dp[i][j] 表示 word1 的前 i 个字符与 word2 的前 j 个字符的最长公共子序列长度dp = [[0] * (n + 1) for _ in range(m + 1)]# 构建 LCS 表格for i in range(1, m + 1):for j in range(1, n + 1):if word1[i - 1] == word2[j - 1]:# 如果当前字符相同，LCS 长度在原基础上 +1dp[i][j] = dp[i - 1][j - 1] + 1else:# 否则，取前一个状态中的较大值dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])# 最长公共子序列长度lcs_len = dp[m][n]# 最少删除次数 = word1 删除非公共部分 + word2 删除非公共部分return m + n - 2 * lcs_len

查看全文

http://www.xdnf.cn/news/4703.html