当前位置：首页 > ops >正文

算法题（196）：最大异或对

ops 2025/9/1 6:39:29

审题：

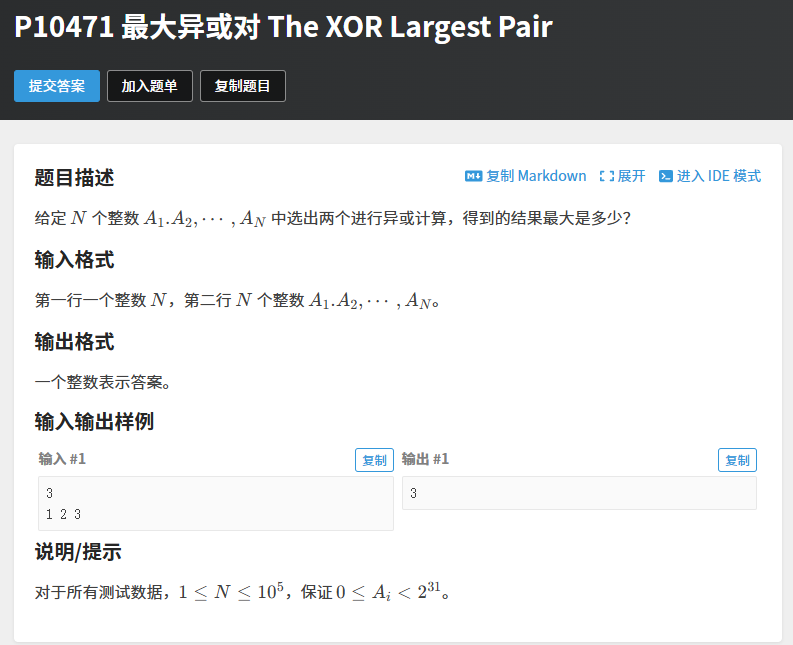
本题需要我们找到n个数中两两进行异或操作后得到的最大结果值输出

思路：
方法一：暴力枚举计算

我们可以利用双层for循环枚举所有计算情况，然后使用异或操作算出结果，结果使用max维护。

但是数据范围达到了1e5，如果用双层for循环会导致时间复杂度高于1e10，一定会超时，那么可不可以减少一个循环，只枚举第一个数？

方法二：贪心+字典树

贪心：

异或操作的最大值是：0111111...1，所以我们只要让选择的第二个数和已经确定的第一个数尽量从左至右和011111...1保持一致即可得到第一个数的最大异或值

eg：

第一个数01101011是确定的数，我们遍历数据而得，为了和max值更接近，我们的数2必须要和数一对应位置的数相反，这样子进行异或操作才能得到1.

本题的数其实有一个隐含条件：num >= 0，所以我们也不用考虑负数的特殊情况

故：让选定的数能够的到最大异或值只需要让与其异或计算的数尽可能在对应位置上与数一相反即可

字典树：

字典树可以存储二进制数且能快速进行查询的数据结构

字典树不仅可以用来进行字符串存储与操作，对于二进制数这种类似字符串的信息也可以进行存储，存储二进制的字典树又叫01字典树

解题：
（1）变量创建与初始化
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N], tr[N * 32][2];
int idx;
a数组：用于存储数据输入值

tr数组：表示字典树结构，由于每个数的二进制表示有32位，所以字符规模是N*32，而字符类型只有0和1，所以字符类型的规模为2

（2）主函数逻辑
int main()
{//数据录入字典树cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];insert(a[i]);}//贪心查找最优解int ret = 0;for (int i = 1; i <= n; i++){ret = max(ret, find(a[i]));}cout << ret << endl;return 0;
}
先用insert函数将数据录入字典树中，然后进行n次find操作将每个数对应的最大异或运算值的出来，利用max进行维护，最后输出ret

（3）insert函数
void insert(int x)
{int cur = 0;for (int i = 31; i >= 0; i--){int path = ((x >> i)&1);if (tr[cur][path] == 0) tr[cur][path] = ++idx;cur = tr[cur][path];}
}
取出每一位对应的数：(x >> 1)&1

先将对应的数据位移动到末尾，然后和1按位与操作，即可取出

eg：

01000...010--->010...001--->1

取出倒数第二位的数：将该数往右移动一位，然后与1进行按位与操作，从而将1取出

（4）find函数
int find(int x)
{int ret = 0, cur = 0;for (int i = 31; i >= 0; i--){int path = ((x >> i) & 1);//先走最优路径if (tr[cur][path^1]){ret |= (1 << i);cur = tr[cur][path ^ 1];}else{cur = tr[cur][path];}}return ret;
}
path取出来的是数一的数，而我们优先需要的是数一的数异或的数，所以先判断path^1的路径是否存在

若存在就将1给到ret对应位置，然后走该路径。

否则就将0给到ret对应位置，然后走非最优路径

ret的计算方法：若是最优路径说明对应位置异或的值是1，否则就为0.

对于1的情况，我们将1给到ret的对应位

对于0的情况：我们不需要进行额外操作，因为ret初始化为每一位都是0

P10471 最大异或对 The XOR Largest Pair - 洛谷