数据分析编程第七步:分析与预测
7.1 销售趋势分析
利用历史销售数据统计月销售额,计算季节化因子,获取去季节化销售数据,然后进行线性拟合,最后预测接下来的某个月的销售额。
第一步:读数,统计月销售额
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(orderDate,quantity,price,discount) |
| 2 | =A1.groups(month@y(orderDate):YMonth;sum(quantity*price*discount):Amount) |
A2 month@y(orderDate) 中选项@y表示返回的是yyyyMM这样格式的数据
第二步:统计月销售额的总均值
| A | |
|---|---|
| 3 | =A2.avg(Amount) |
第三步:计算去季节化因子
| A | |
|---|---|
| 4 | =A2.groups(YMonth%100:Month;avg(Amount)/A3:seasonal_factor).keys@i(Month) |
A4 YMonth%100 表示 YMonth 除以 100 的余数,这样返回的就是 MM 这样格式的整数,按这样的月份数据分组汇总,可以分别统计 1 月的均值、2 月的均值……,用当前月份的均值除以 A3(总均值),即可获得当前月份的季节因子。
keys@i(Month) 表示对当前序表设置主键字段和索引字段为 Month,方便后续按月份查找季节因子,效率更高。选项 @i 表示同时设置索引字段,如果无 @i 选项,则仅设置主键字段。
第四步:计算去季节化后的月销售额
| A | |
|---|---|
| 5 | =A2.derive((YMonth\100-2020)*12+ YMonth%100:period_num,Amount/A4.find(YMonth%100).seasonal_factor:deseasonalized) |
A5 (YMonth\100-2020)*12+ YMonth%100表达式的含义:以 2020 年 1 月份为 1,之后月份递增,从而获得一个月份的自然数列,作为横轴
Amount/A4.find(YMonth%100).seasonal_factor 表达式的含义:用当前月份的月销售额除以当前月份的季节因子,返回值作为去季节化的销售额。其中 A4.find(YMonth%100) 表示从 A4 序表中用其主键索引查找 YMonth%100 对应的记录,因此 A4 必须事先建主键和索引。
A5 的运行结果:
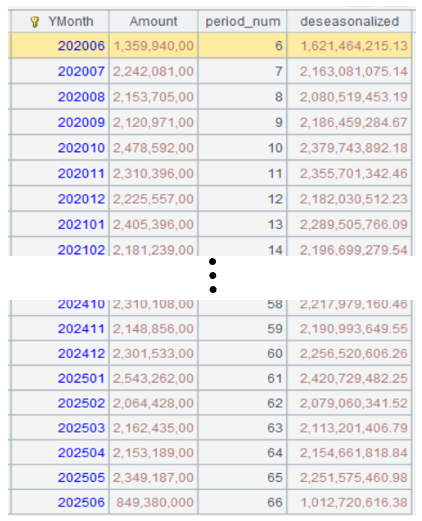
第五步:线性拟合
| A | |
|---|---|
| 6 | =linefit(A5.(period_num),A5.(deseasonalized)) |
A6 将 A5 中算得的月份的数列和对应月份的去季节化月销售额进行线性拟合,其中 linefit 为线性拟合函数。本例中两个参数均为一维的向量,因此对应的方程为:y=ax,函数中第一个参数为 x,第二个参数为 y,返回值为 x 的系数 a。
第六步:预测未来的月销售额
| A | |
|---|---|
| 7 | =A6*67 |
| 8 | =A7*A4.find(67%12).seasonal_factor |
A7 从前面 A5 的运行结果可以看出,总数据是到 period_num 为 66,因此我们预测 67 的月销售额,用 A6 乘以 67,即可得到 67 的去季节化销售额。
A8 用 A7 中的去季节化销售额乘以季节因子,就可以得到 67 对应的真正月销售额。
知识点:linefit 函数
线性拟合(Linear Fitting)是一种通过线性模型(通常是一条直线)来近似描述数据集中变量之间关系的统计方法。它假设因变量(目标变量)与一个或多个自变量(特征变量)之间存在线性关系,并通过最小化误差来找到最佳拟合的线性方程。
核心概念
1. 线性模型:
- 一元线性拟合(单变量):形式为 y=ax+b,其中:
- y 是因变量
- x 是自变量
- a 是斜率(回归系数)
- b 是截距
- 多元线性拟合(多变量):形式为 y=a1x1+a2x2+⋯+b,适用于多个自变量的情况。
2. 目标:
- 找到参数(斜率和截距),使得模型预测值与实际数据点的误差最小(通常使用最小二乘法)。
3. 最小二乘法:
- 通过最小化残差平方和(预测值与真实值之差的平方和)来确定最佳拟合直线。
函数语法
linefit(A,Y) 用最小二乘做线性拟合,系数矩阵为A,常数Y
@1 当Y是向量时,返回向量而非矩阵
应用场景
- 预测房价与面积的关系。
- 分析广告投入与销售额的关联。
- 实验数据的趋势分析。
优缺点
- 优点:简单、计算高效、易于解释。
- 缺点:对非线性关系拟合效果差,易受异常值影响。
7.2 销售趋势分析 2
上例仅对月份和销售额做分析,实际应用中,销售额和产品价格也会有很大的依赖关系,同时还会有系数的影响,即上例中提到的方程 y=ax+b 中的截距 b,本例就来分析销售额和月份、产品价格之间的关系,对应的方程是 y=a1x1+a2x2+b,其中 x1代表月份,x2代表产品价格。
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(orderDate,quantity,price,discount) |
| 2 | =A1.groups(month@y(orderDate):YMonth,price;sum(quantity*price*discount):Amount) |
| 3 | =A2.avg(Amount) |
| 4 | =A2.groups(YMonth%100:Month,price;avg(Amount)/A3:seasonal_factor).keys@i(Month,price) |
| 5 | =A2.derive((YMonth\100-2020)*12+ YMonth%100:period_num, Amount/A4.find(YMonth%100,A2.price).seasonal_factor:deseasonalized) |
| 6 | =linefit@1(transpose([A5.(period_num),A5.(price),A5.(1)]),A5.(deseasonalized)) |
| 7 | =file(“product.csv”).import@tc(productID,listPrice) |
| 8 | =A7.derive((67*A6(1)+listPrice*A6(2)+A6(3))*A4.find(67%12,listPrice).seasonal_factor:Predicted) |
A2、A4 分组汇总时加上产品价格price字段,A4 的主键索引也加上 price 字段
A6 linefit 函数加上 @1 选项,表示返回值是个序列而非矩阵。参数transpose([A5.(period_num),A5.(price),A5.(1)])表示由period_num、price、数列1三个序列组成的矩阵,数列 1 表示截距 b*1。
A6 的运行结果:
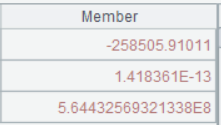
A7 从产品表读取 productID,listPrice
A8 预测下个月 (即月份期数为 67) 几种不同价格产品的销售额,其计算公式为 y=a1x1+a2x2+b,其中 a1、a2、b 分别对应 A6 返回的三个值,x1为月份期数,x2为产品列表价
A8 的运行结果:
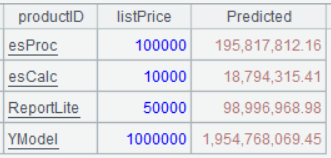
7.3 销售数量与折扣的相关性分析
销售数量是否与折扣有关?订货量大折扣大吗?相关性分析可以回答这些问题:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@ct(quantity,discount) |
| 2 | =pearson (A1.(discount),A1.(quantity)) |
A2 计算折扣与销售数量之间的 Pearson 相关系数
知识点:pearson 函数
Pearson 相关系数(记作 r)是一种衡量两个连续变量之间线性关系强度和方向的统计量,取值范围为 [−1,1]。
核心概念
1. 定义:
- 衡量两个变量 X 和 Y 的线性相关性。
- 计算公式:
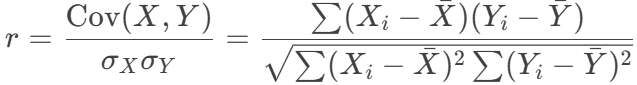
- 其中:
- Cov(X,Y) 是协方差
- σX,σY 是标准差
是均值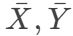
2. 取值范围:
- r=1:完全正相关(变量呈严格递增线性关系)
- r=−1:完全负相关(变量呈严格递减线性关系)
- r=0:无线性相关性(但可能有非线性关系!)
3. 特点:
- 仅适用于线性关系,无法捕捉非线性关联(如 y=x2y=x2)。
- 对异常值敏感,极端值可能显著影响 rr。
- 取值范围在 [−1,1][−1,1],绝对值越大,相关性越强。
函数语法
pearson(A,B) 计算向量A和B的 pearson 相关系数,B省略时用 to(A.len())
@r 计算 r2,即 pearson(norm@0(A),norm@0(B))
@a(…;k) 计算调整后的 r2,自由度为k
如何解释 Pearson 相关系数?
| rr值范围 | 相关性解释 | ||
|---|---|---|---|
| 0.8< | r | < 1 | 强相关 |
| 0.5< | r | < 0.8 | 中等相关 |
| 0.3< | r | < 0.5 | 弱相关 |
| 0 < | r | < 0.3 | 极弱或无关 |
7.4 分析产品之间的销量均值差异
产品 esProc 和其它产品之间的销量均值是否存在较大差异?使用 t-test 分析即可得到答案:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(product,quantity) |
| 2 | =ttest_p(A1.(if(product==“esProc”:0;1)),A1.(quantity)) |
A2 ttest_p 函数为 SPL 中的 t-test 分析函数,输入参数为两组序列,第一组序列为 0、1 的二值序列,第二个序列为对应要分析的数值,该函数会自动根据 0、1 把第二个序列拆成两组数进行比较。
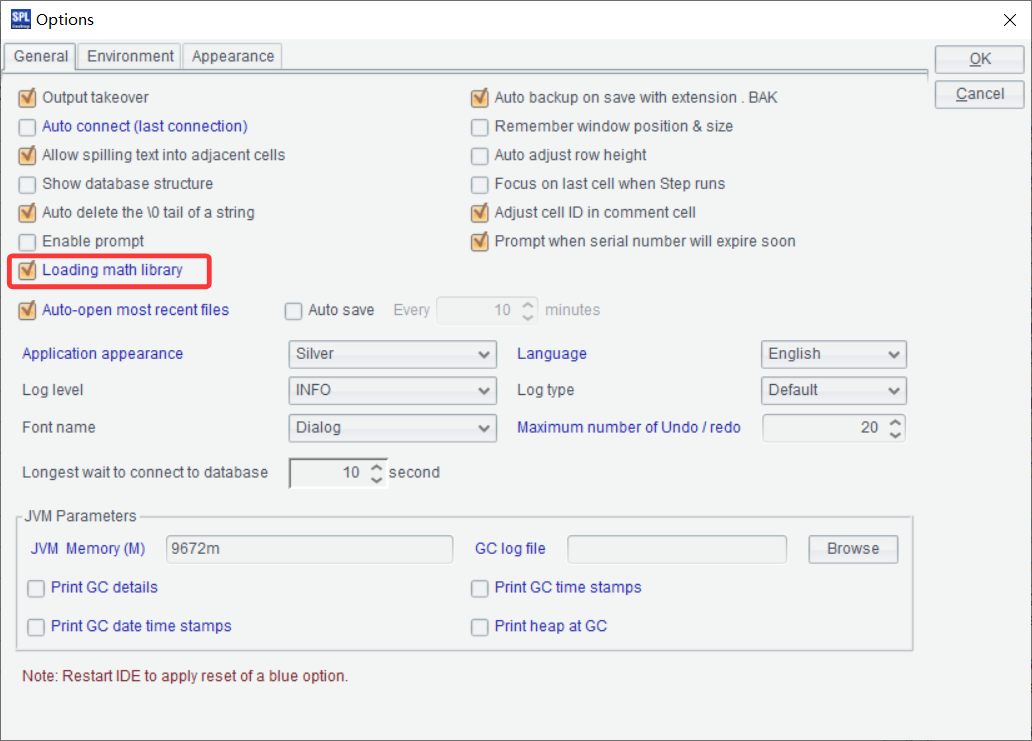
ttest_p 函数在外部库中,需要先加载外部库才能使用,加载步骤:
1、 点击 Tool/Options
2、 勾选 Loading math library
知识点:ttest_p 函数
T 检验是一种统计假设检验方法,用于判断两组数据的均值是否存在显著差异。它基于t 分布(Student’s t-distribution),适用于样本量较小(通常 n<30)且总体方差未知的情况。
核心概念
- 目的:比较两组数据的均值,判断差异是否由随机误差引起,还是具有统计学意义。
- 适用条件:
- 数据近似服从正态分布(或样本量足够大,依赖中心极限定理)。
- 方差齐性(某些 T 检验要求组间方差相等)。
- 结果输出:
- p 值:若 p<0.05(通常显著性水平),则认为差异显著。
函数语法:
ttest_p(X, Y) T 检验求p值。
应用举例
- 比较 A/B 测试中两组用户的点击率是否有显著差异。
- 比较同一组样本在不同条件下的差异(如服药前后的血压变化)。
- 检验减肥训练前后学员体重的变化是否显著。
如果想分析所有产品之间的销量均值差异,可以使用 ANOVA 分析,在 SPL 中为 fisher_p 函数:
| A | |
|---|---|
| 1 | =file(“sales.csv”).import@tc(product,quantity) |
| 2 | =fisher_p(A1.(product),A1.(quantity)) |
A2 fisher_p 函数适合多组数据之间的均值差异比较,不需要将数据拆成多组,而是直接把分组字段的值序列和数值序列传给 fisher_p 函数即可,函数会自动根据分组字段将数值拆成多组进行比较
知识点:fisher_p 函数
fisher_p 函数采用 ANOVA(Analysis of Variance,方差分析),是一种用于比较三个或更多组均值是否存在显著差异的统计方法。它的核心思想是通过分析数据中的方差(变异性)来判断组间差异是否显著大于组内差异。
核心概念
(1) 为什么要用 ANOVA?
- T 检验的局限性:T 检验只能比较两组均值,而多组比较时,若逐一两两比较会增加Type I 错误(假阳性)的概率。
- ANOVA 的优势:一次性检验多组均值差异,控制整体错误率。
(2) 基本假设
- 正态性:各组数据近似服从正态分布(或样本量足够大)。
- 方差齐性(Homogeneity of Variance):各组的方差应相近(可通过 Levene 检验判断)。
- 独立性:观测值之间相互独立(如不同组的样本无关联)。
(3) 假设检验
- 原假设(H₀):所有组的均值相等(μ₁ = μ₂ = … = μₖ)。
- 备择假设(H₁):至少有两组的均值不等。
函数语法
fisher_p(X, Y) F 检验求p值。
ANOVA vs T 检验
| 对比项 | ANOVA | T 检验 |
|---|---|---|
| 比较组数 | ≥3 组 | 2 组 |
| 适用场景 | 多组均值差异 | 两组均值差异 |
| 后续分析 | 需要事后检验 | 直接解释结果 |
| 统计量 | F 值 | t 值 |
4. 结果解释
- p 值:
- 若 p<0.05,拒绝 H₀,认为至少有两组均值不同。
- 若 ANOVA 显著,需通过事后检验确定具体差异组。
7.5 客户交易数据的 RFM 分析
通过评估客户购买行为,对交易数据进行 RFM(最近一次消费、消费频率、消费金额)分析。通过定义一个自定义函数,它接收三个输入参数:交易数据、参考日期。其中最近消费时间(R)计算为客户最后一次购买距今的天数,数值越小越好;消费频率(F)是购买总次数,数值越高表示互动越频繁;消费金额(M)指总支出金额,花费越多代表客户价值越高。为统一量纲,每个分量会被排序并转换为 0 到 5 分的标准分——最近消费时间按降序排列(因近期交易更理想),而消费频率和消费金额按升序排列(因更多消费次数和更高金额更优)。
| A | B | |
|---|---|---|
| 1 | =file(“sales.csv”).import@ct(customer,orderDate,quantity,price,discount) | |
| 2 | func rfm_score(data,current_date) | |
| 3 | =data.groups(customer; interval(max(orderDate),current_date):recency, count(1):frequency, sum(quantity*price*discount):monetary) | |
| 4 | =B3.len() | |
| 5 | =B3.derive(:r_score,: f_score,:m_score) | |
| 6 | =B5.sort(recency:-1).run(r_score=rank(recency)/B4*5) | |
| 7 | =B5.sort(frequency).run(f_score=rank(frequency)/B4*5) | |
| 8 | =B5.sort(monetary).run(m_score=rank(monetary)/B4*5) | |
| 9 | return B5 | |
| 10 | =rfm_score(A1,now()) | |
A1 从文件 sales.csv 读数
A2 定义了一个函数,函数名为 rfm_score,参数为 data, current_date
B3 将输入参数 data 按客户分组,统计最近一次下单距离参考日期的时长,下单次数、总下单金额
B4 统计 B3 的总记录数
B5 添加三个字段 r_score,f_score,m_score
B6-B8 分别计算 r_score,f_score,m_score 三个字段的值,表达式 rank(recency)/B4*5 的含义是:按 recency 计算排名,然后除以总记录数,获得位次占比,最后乘以 5,返回值即为 0-5 分。其余两个字段类似,只是排序规则相反。
B9 函数返回结果
A10 调用自定义函数 rfm_score,传入参数 A1,now()。
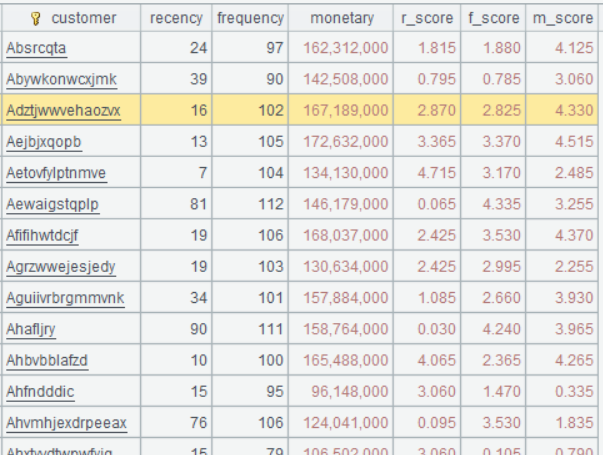
A10 的运行结果:
知识点:什么是代码块?
如下图所示:
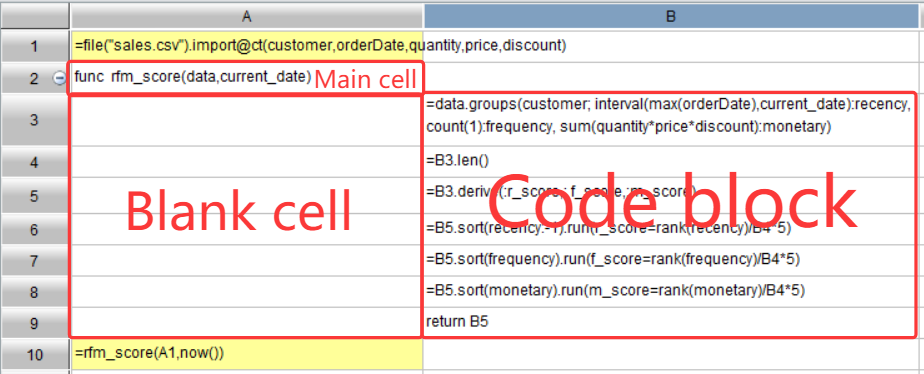
A2 为非空单元格,其下单元格片区 A3:A9 均为空白格,A10 非空,那么 B3:B9 单元格称为以 A2 为主格的代码块。
代码块的核心特性
- 缩进敏感:
- 相同缩进层级属于同一代码块
- 通常使用一个空白单元格作为缩进单位
- 作用域规则:
- 代码块内定义的变量只在块内有效
- 可以访问外部作用域的变量
- 流程控制:
- 分支和循环语句通过缩进形成代码块
主要应用场景
1. 函数定义
| A | B | C | |
|---|---|---|---|
| 1 | =func factorial(n) | ||
| 2 | if n==1 | ||
| 3 | return 1 | ||
| 4 | else | ||
| 5 | return n*factorial(n-1) | ||
2. 条件判断
| A | B | |
|---|---|---|
| 1 | =x=10 | |
| 2 | if x>5 | |
| 3 | =“>5” | |
| 4 | else | |
| 5 | =“<=5” | |
3. 循环结构
| A | B | |
|---|---|---|
| 1 | =i=1 | |
| 2 | for i<=5 | |
| 3 | >output=output+" "+string(i) | |
| 4 | >i=i+1 | |
4. 异常处理
| A | B | |
|---|---|---|
| 1 | try | |
| 2 | =1/0 | |
| 3 | if A1!=null | |
| 4 | =“error” | |
| 5 | else | |
| 6 | =“correct” | |
多级代码块示例
| A | B | C | D | |
|---|---|---|---|---|
| 1 | =func process(data) | |||
| 2 | =result=[] | |||
| 3 | for data | |||
| 4 | if #B3%2==0 | |||
| 5 | =result.insert(0,B3) | |||
| 6 | return result | |||
代码块执行特点
- 独立执行环境:每个代码块有独立的变量作用域
- 返回值:最后一个表达式的值作为代码块的返回值
- 网格坐标引用:可以通过单元格坐标 (如 A1) 跨代码块引用值
与 Excel 公式的区别
- 结构化编程:支持真正的代码块和流程控制
- 变量作用域:比 Excel 的单元格引用更灵活
- 函数特性:支持递归、高阶函数等高级特性
集算器 SPL 的这种基于网格和缩进的代码块设计,既保留了类似 Excel 的直观性,又提供了完整的编程能力,非常适合处理复杂的数据计算任务。
知识点:自定义函数
基本语法:
| A | B | |
|---|---|---|
| 1 | =func funcName(arg1,arg2,……) | |
| 2 | Indented Function Block |
完整函数定义示例
1. 基础函数
| A | B | |
|---|---|---|
| 1 | =func add(a,b) | |
| 2 | =a+b | |
| 3 | return B2 | |
| 4 | =add(3,5) | |
A1 函数定义开始
B2 函数体(缩进一格)
B3 返回值(可省略,默认返回最后表达式值)
A4 调用函数,返回 8
2. 带默认参数的函数
| A | B | |
|---|---|---|
| 1 | =func greet(name=“Guest”,greeting=“Hello”) | |
| 2 | =greeting+“,”+name+“!” | |
| 3 | return B2 | |
| 4 | =greet() | |
| 5 | =greet(“John”) | |
| 6 | =greet(“Mary”,“Hi”) | |
A4 返回 "Hello, Guest!"
A5 返回 "Hello, John!"
A6 返回 "Hi, Mary!"
函数代码块特性
- 缩进规则:
- 函数声明后所有缩进相同空格数的单元格都属于函数体
- 通常使用1 个空格作为标准缩进量
- 作用域控制:
- 函数内部变量与外部隔离
- 可以访问外部全局变量(需谨慎使用)
- 多语句执行:
- 函数体可以包含多个按顺序执行的语句
7.6 根据 RFM 分析结果,将客户分成五类
根据上例中 RFM 的分析结果,将客户分成五类,采用两种分类方法,一种是直接按 r_score,f_score,m_score 三种分值分类,另一种是按加权过的分值分类
方法一:
| A | |
|---|---|
| … | // 接上例 |
| 11 | =kmeans(A10.([r_score,f_score,m_score]),5) |
| 12 | =kmeans(A11,A10.([r_score,f_score,m_score])) |
A11 将客户的 r_score,f_score,m_score 分值按 kmeans 聚类方法,把客户分成五类。kmeans 函数是 SPL 中的采用经典的无监督学习聚类算法函数,后面会详细介绍。
A12 根据 A11 的聚类结果,返回每个客户归属的分类号,分类号相同的客户,意为同一类
A12 的运行结果:
方法二:给三种分值加权重,其中销售额最重要,权重为 3,购买次数次之,权重为 2,最近购买日期权重为 1,重新分类:
| A | |
|---|---|
| … | // 接上例 |
| 11 | =kmeans(A10.([r_score,f_score*2,m_score*3]),5) |
| 12 | =kmeans(A11,A10.([r_score,f_score*2,m_score*3])) |
A12 的运行结果为:
知识点:kmeans 函数
kmeans 算法概述
K-means 是一种经典的无监督学习聚类算法,它将数据集划分为 K 个簇 (cluster),使得同一簇内的数据点相似度高,而不同簇的数据点相似度低。
kmeans 函数语法
kmeans(X, k) 用 k-means 聚类算法将矩阵 X 分成 k 个簇,返回拟合模型 B
kmeans(B, A) 用 k-means 聚类算法,根据拟合模型 B,分析数据A,返回 A 归属的簇序号
kmeans 算法步骤
- 初始化:随机选择 K 个点作为初始质心 (中心点)
- 分配步骤:将每个数据点分配到最近的质心所在的簇
- 更新步骤:重新计算每个簇的质心 (取簇中所有点的均值)
- 重复:重复步骤 2-3 直到质心不再显著变化或达到最大迭代次数
kmeans 的应用场景
1. 客户细分
- 根据购买行为、人口统计特征对客户进行分组
- 用于精准营销和个性化推荐
2. 图像压缩
- 将图像颜色减少到 K 种代表性颜色
- 减少存储空间同时保持视觉质量
3. 文档分类
- 对文本文档进行聚类
- 发现文档集合中的主题群组
4. 异常检测
- 识别远离任何簇中心的异常点
- 用于欺诈检测、网络入侵检测等
5. 市场细分
- 根据地理位置、消费习惯等对市场进行划分
- 帮助制定区域化营销策略
kmeans 的优缺点
优点:
- 简单、易于理解和实现
- 计算效率高,适用于大规模数据集
- 对于球形簇结构的数据效果良好
缺点:
- 需要预先指定 K 值
- 对初始质心选择敏感
- 对噪声和异常值敏感
- 只能发现球形簇,难以处理复杂形状的簇
