《软件工程导论》实验报告四 详细设计工具
目 录
一、实验目的
二、实验环境
三、学时分配
四、实验内容与步骤
五、实验问题及解决方法
六、实验心得
一、实验目的
1. 了解软件详细设计阶段的目的、任务和结构化程序设计的概念,针对给定问题,能使用软件建模工具进行业务流程的绘制,描述程序处理过程。
2. 掌握程序处理过程使用到的工具,包括程序流程图、N-S图、PAD图,熟悉结构化程序设计的基本流程。
3. 掌握应用Visio等业界常用的建模工具的基本使用方法和基本绘图操作,选择一种并熟练使用,会使用该工具针对具体问题绘制图形。
二、实验环境
1. 操作系统:Windows 操作系统。
2. 操作软件:WPS 文档编辑器、建模工具 boardmix。
3. 硬件设备:笔记本电脑一台。
三、学时分配
学时分配: 2 学时。
四、实验内容与步骤
1. 根据以下描述,绘制出对应的程序流程图。
阶乘的算法如下:
- 输入一个数 n;
- 赋值 s=1,t=1;
- 计算 s=s*t,t = t +1;
- 比较 t 是否大于 n ,若大于,跳至 5;否则返回 3;
- 输出 s。
请绘制出阶乘算法程序的程序流程图。
由上述的阶乘算法可知,程序流程图中存在一个输入为“输入n”,然后将s和t分别进行赋值处理后通过计算式s=t*s和计算式t=t+1对s和t分别进行计算处理操作,得到对应的结果后进行t和n的判断,如果t>n则直接输出对应的s即可,否则继续进行计算式的处理操作,直到t>n后输出对应的s,对应的阶乘算法程序流程图如图4-1所示:
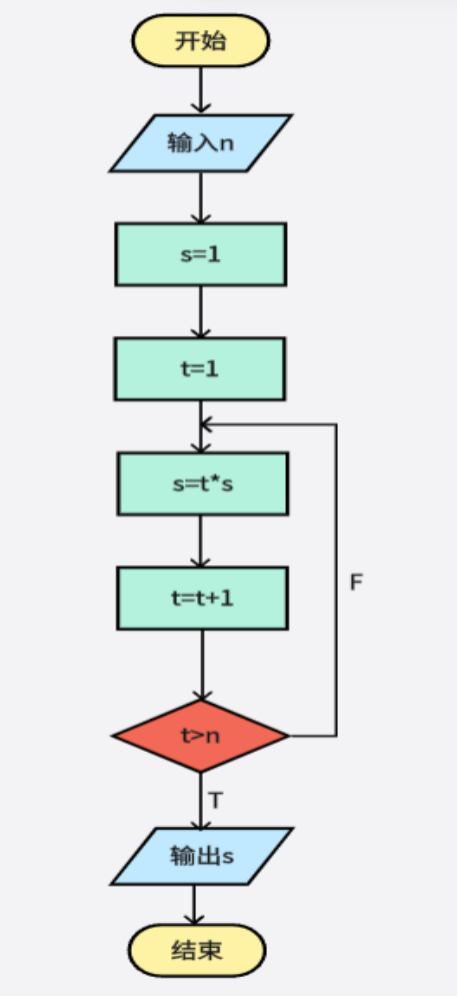
图4-1 阶乘算法程序流程图
2. 根据以下描述,绘制出对应的程序流程图。
求 1 到 100 所有整数总和的 c 语言代码如下:
int main() {
int sum = 0;
int i;
for (i = 1; i <= 100; i++) {
sum += i;
}
printf("从1到100的整数总和是: %d\n", sum);
return 0;
}
请绘制出该代码程序的流程图。
由以上进行前100求和的c语言代码可知先进行sum=0,i=1的赋值处理,将计算后的值进行i<=100的判断操作,如果符合条件则继续进行计算式sum=sum+i和i=i+1的计算处理操作,直到不符合判断的条件后输出sum的最终计算结果,对应的前100求和程序流程图如图4-2所示:
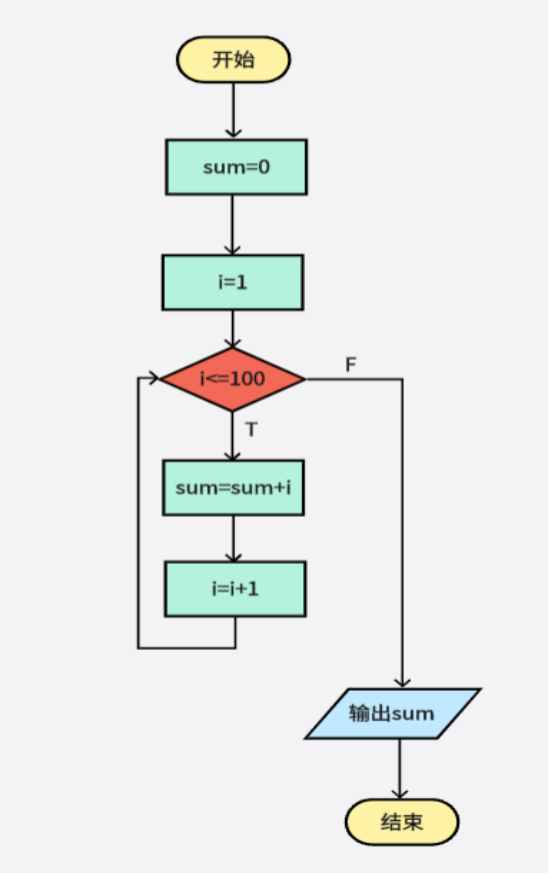
图4-2 前100求和程序流程图
3. 请根据题目 2 的描述绘制出对应的 N-S 图。
由题二绘制的前100求和程序流程图可知需要先进行sum和i赋值处理操作,然后进行i的值是否小于等于100的判断,如果符合条件则进行sum=sum+i和i=i+1的计算,直到最后i的值大于100时进行最终结果sum的输出,对应的前100求和N-S图如图4-3所示:
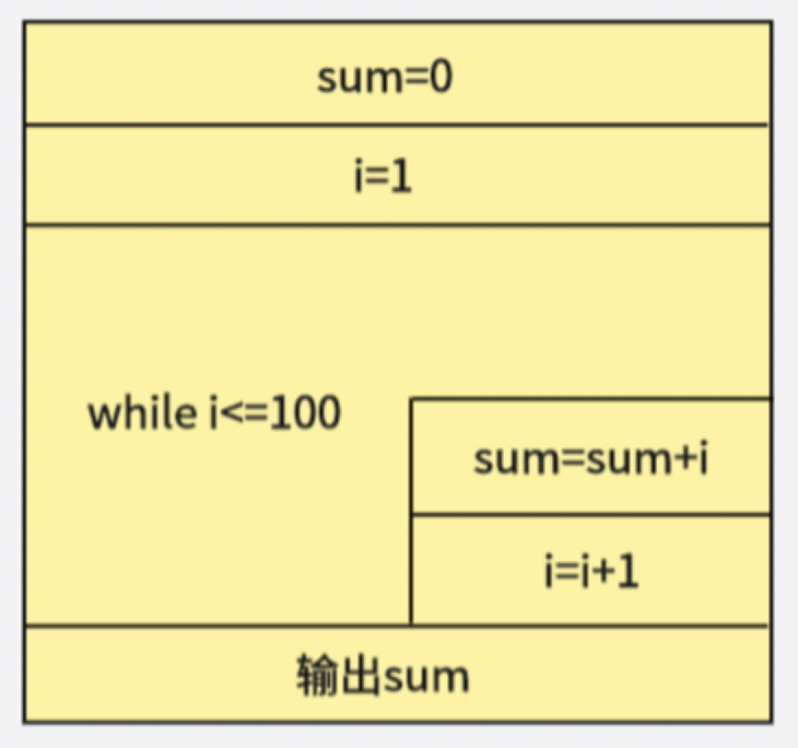
图4-3 前100求和N-S图
4. 根据以下描述,绘制出对应的程序流程图和 N-S 图。
输入三角形三边长 a、b、c,判断三边构成的是等边,等腰,还是一般三角形。
在进行三角形类型的判断时先输入三角形对应的三条边的长度,然后先判断其中任意两条边是否相等(例如先进行a边和b边的判等操作),如果其中不存在任意两条边相等则为一般三角形;在上一步判断符合条件的基础上进行其中一条判断边和另一条边的判等操作(例如进行a边和c边的判等操作),如果判等条件满足则为等边三角形,否则为等腰三角形;在第一步a边和b边判等条件不满足的前提下进行其中一个判断边和另一个边的判等操作(例如进行a边和c边的判等操作),如果符合条件则为等腰三角形,否则继续进行b边和c边的判等操作,如果判等条件满足则为等腰三角形,否则为一般三角形,对应的三角形类型判断程序流程图如图4-4所示:
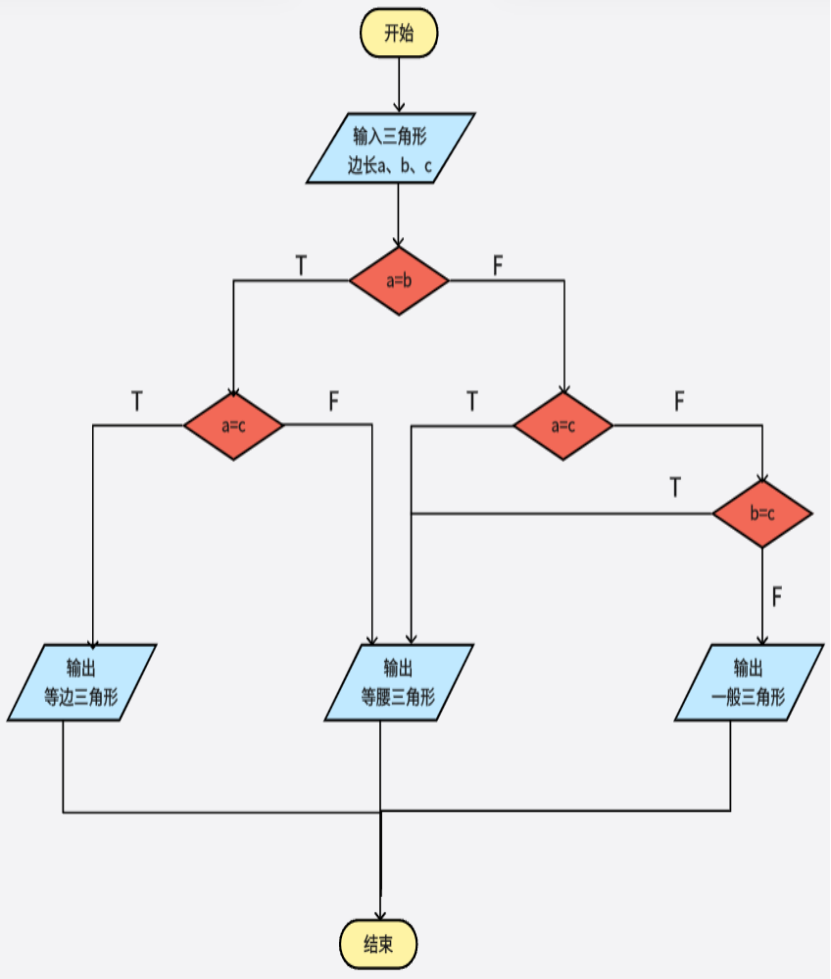
图4-4 三角形类型判断程序流程图
依据上述三角形类型判断程序流程图可知,在进行三角形类型的判断时先输入三角形对应的三条边a、b、c,然后先进行a边和b边的判等操作,如果满足条件则进行a边和c边的判等操作,如果满足条件则输出三角形的类型为等边三角形,否则输出三角形的类型为等腰三角形;在第一步判等条件不满足的情况下进行a边和c边的判等操作,如果满足条件则为等腰三角形,否则继续进行b边和c边的判等操作,如果满足条件则输出三角形的类型为等腰三角形,否则输出三角形类型为一般三角形,对应的三角形类型判断N-S图如图4-5所示:
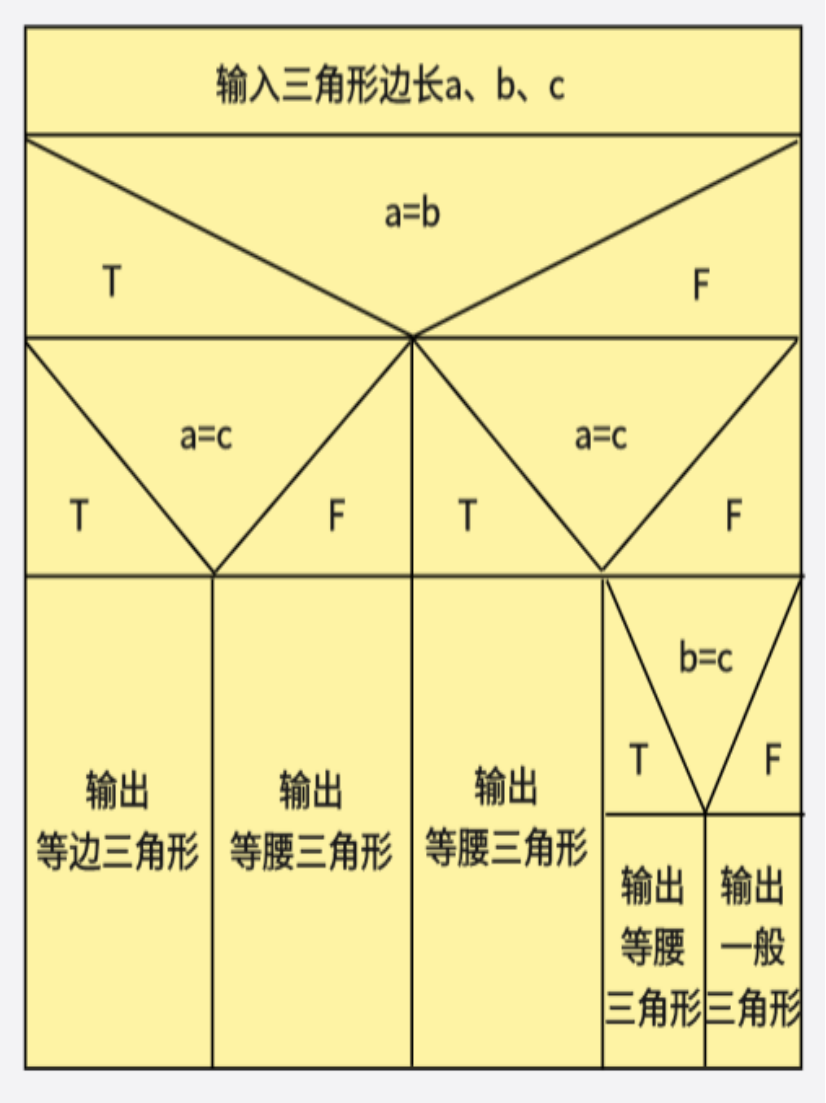
图4-5 三角形类型判断N-S图
5. 请根据题目 1 的描述绘制出对应的 PAD 图。
由题目一的阶乘算法可知,先顺序进行输入n、赋值s=1、赋值t=1的操作,然后进入直到型循环t>n中,在直到型循环中顺序执行s=s*t和t=t+1的运算操作,最后输出最终结果s的值后结束程序,对应的阶乘算法PAD图如图4-6所示:
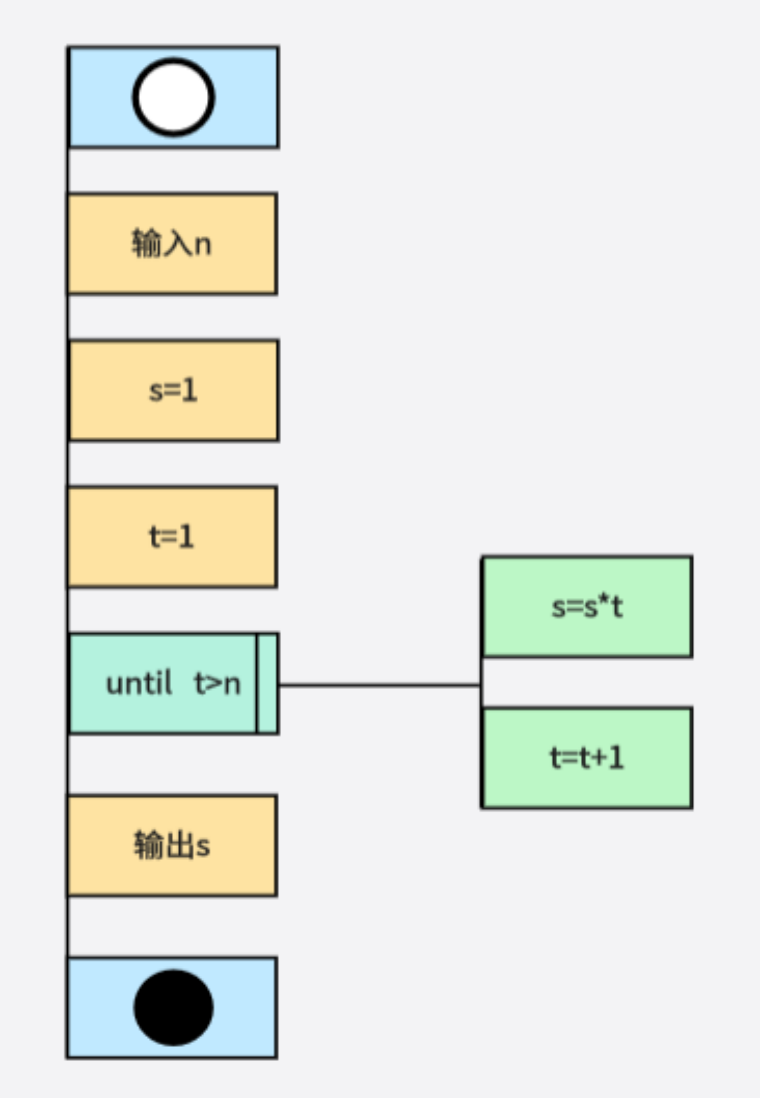
图4-6 阶乘算法PAD图
五、实验问题及解决方法
(1)实验问题:在进行循环判断和条件判断的时候出现判断失误。
解决方法:在流程图中使用条件判断的菱形框表示,使用箭头表示条件的真假分支;对于循环结构使用循环的圆角矩形框表示,并使用箭头表示循环的开始和结束。
(2)实验问题:在流程图的绘制过程中复杂的判断和循环结构难以处理。
解决方法:对于复杂的判断和循环结构,可以使用条件分支和循环的嵌套,使用合适的图形和标记来表示层次结构和关系,可以使用子流程或子图形来表示复杂的逻辑。
(3)实验问题:对多个并行的事务进行处理操作。
解决方法:用并行处理的图形表示,如平行的箭头路径或平行的矩形框,以表示多个并行处理步骤。
(4)实验问题:精确表示函数或者子程序之间的调用关系。
解决方法:使用矩形框中的函数名称或子程序名称,并使用箭头连接到相应的调用位置。
(5)实验问题:对程序运行过程中可能出现的异常进行处理。
解决方法:使用带有异常处理标记的矩形框,并使用箭头连接到异常处理步骤。
(6)实验问题:对并发和并行两种情况进行精确处理。
解决方法:使用平行的箭头路径或平行的矩形框,以表示并发或并行的处理步骤。
(7)实验问题:在绘制程序流程图时进行复杂条件的判断。
解决方法:使用分支结构(如if-else语句)来表示复杂的条件判断,根据条件的不同结果,使用不同的箭头路径连接到相应的处理步骤。
(8)实验问题:在程序流程图的绘制过程中出现算法逻辑错误或运算精度问题。
解决方法:需要仔细检查算法逻辑,确保输入的三边长能够正确地判断出三角形的类型。同时需要注意运算精度问题,可以使用浮点数进行计算,避免整数除法造成的精度损失。
(9)实验问题:在N-S图中,过早或错误地使用并行符号。
解决方法:确保在所有步骤都按顺序执行后才使用并行符号。
(10)实验问题:流程或层次结构中的步骤没有注释,导致难以理解。
解决方法:为每个步骤添加注释,解释其目的和功能。
(11)实验问题:在绘制N-S图时出现流程不明确、逻辑不清晰或图形不美观。
解决方法:仔细分析算法流程,明确每个步骤的功能和作用,并在N-S图中清晰地表达出来。同时注意图形的美观性和易读性,可以使用不同的颜色或形状来区分不同的步骤或模块。
(12)实验问题:在绘制PAD图时出现层次不清晰、结构不完整或图形难以理解。
解决方法:将算法按照模块进行划分,并在PAD图中清晰地表达出各个模块之间的关系和层次结构。同时注意图形的简洁性和易理解性,避免使用过多的线条和符号造成图形复杂化。
六、实验心得
1、通过绘制阶乘算法的程序流程图和N-S图,让我清晰地看到算法的流程和各个步骤的实现方式,有助于我更好地理解算法。让我学会了如何将复杂的程序分解为简单的步骤,并使用图形来表示程序的流程和实现方式。
2、通过绘制程序流程图和N-S图以及PAD图,让我学会了如何更好地组织和思考程序的逻辑结构和实现方式,有助于我更好地设计和实现程序,更好地遵循编程规范和实践,提高代码的可读性和可维护性。
3、在绘制流程图的过程中,让我深刻理解了程序流程的重要性和可视化的价值。流程图将复杂的程序逻辑简化为图形元素,有助于我们更清晰地把握程序的运行流程。同通过流程图可以更方便地进行程序调试和优化。
4、N-S图是一种将程序逻辑可视化的工具,它使用矩形和箭头表示程序中的各个步骤。通过N-S图,我们可以更清晰地看到程序的执行流程和数据流。此外N-S图还可以帮助我们发现程序中的潜在错误和优化空间。
5、PAD图是一种用于描述程序结构的工具,它使用树形结构表示程序的层次关系,让我更加理解了程序的结构和模块化设计的重要性,更好地组织程序的结构和流程。
