2025杭电多校第七场 矩形框选、伤害冷却比 个人题解

伤害冷却比

#数学

题目

思路

令$a=\frac{K}{N}$，则有$f(x)=x\left(\lfloor \frac{a}{x}\rfloor +1\right)$
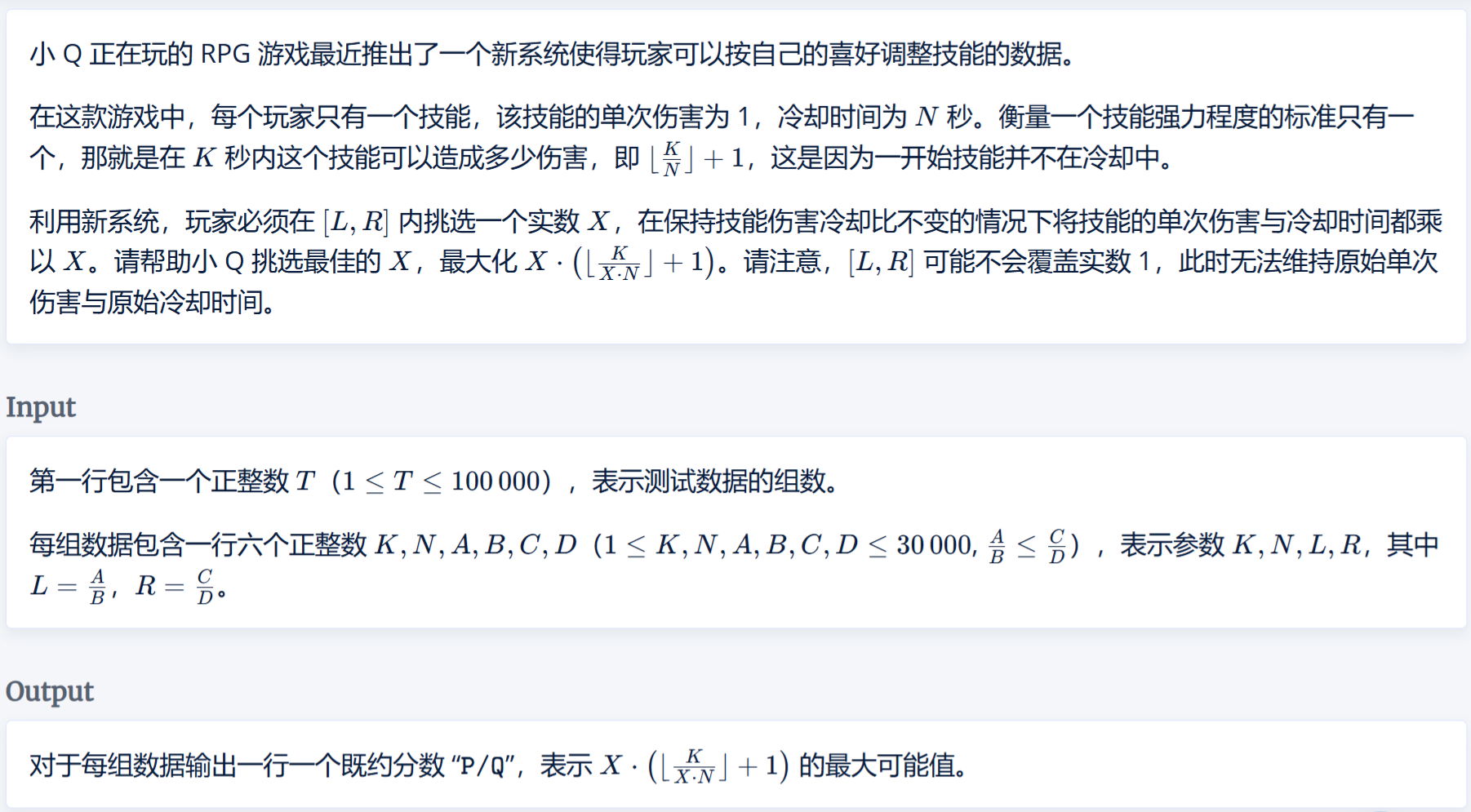
大致画出图像，可得下图

若要求区间$[L,R]$上的最大值，则需要求出$f(R)$与红线蓝线交点值之间的最大值

为了求出交点，联立两个方程：
$$\begin{array}{rl}x+a& =x\left(\lfloor \frac{a}{x}\rfloor +1\right)\\ & \\ x+a& =x\lfloor \frac{a}{x}\rfloor +x\\ & \\ \frac{a}{x}& =\lfloor \frac{a}{x}\rfloor \\ & \\ \exists n\in & Z,\frac{a}{x}=n\\ & \\ \therefore x=\frac{a}{n}& ,n=1,2,3,\dots \end{array}$$
因此可以找到距离$R$最近的$x_0=\frac{a}{n}$，其中$n=\lceil \frac{a}{R}\rceil$
再将此$x_0$带入$y=x+a$中，即可得到区间$[L,R]$上交点的最大值啦

随后将$R$带入$f(x)$中，比较二者大小约分输出即可

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<unordered_set>
#include<string.h>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define mid ((l+r)>>1)
#define double long double
#define int ll
int gcd(int a,int b){if(b==0)return a;return gcd(b,a%b);
}void eachT(){int K,N,A,B,C,D;cin>>K>>N>>A>>B>>C>>D;int n=ceil(1.0*(K*D)/(N*C));double x=1.0*K/(N*n);double ans1=x+(1.0*K/N);double L=1.0*A/B;if(L>x)ans1=-1;double ans2=1.0*C/D*(K*D/(N*C)+1);if(ans1>=ans2){int g=gcd(K*(1+n),N*n);cout<<K*(1+n)/g<<"/"<<N*n/g<<'\n';}else{int g=gcd(C*(K*D/(N*C)+1),D);cout<<C*(K*D/(N*C)+1)/g<<"/"<<D/g<<'\n';}
}signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);int t=1;cin>>t;while(t--)eachT();
}

---

矩形框选

#线段树 #扫描线 #二维数点 #差分 #区间最值

题目

思路

先讲一讲二维数点的一个常用技巧：

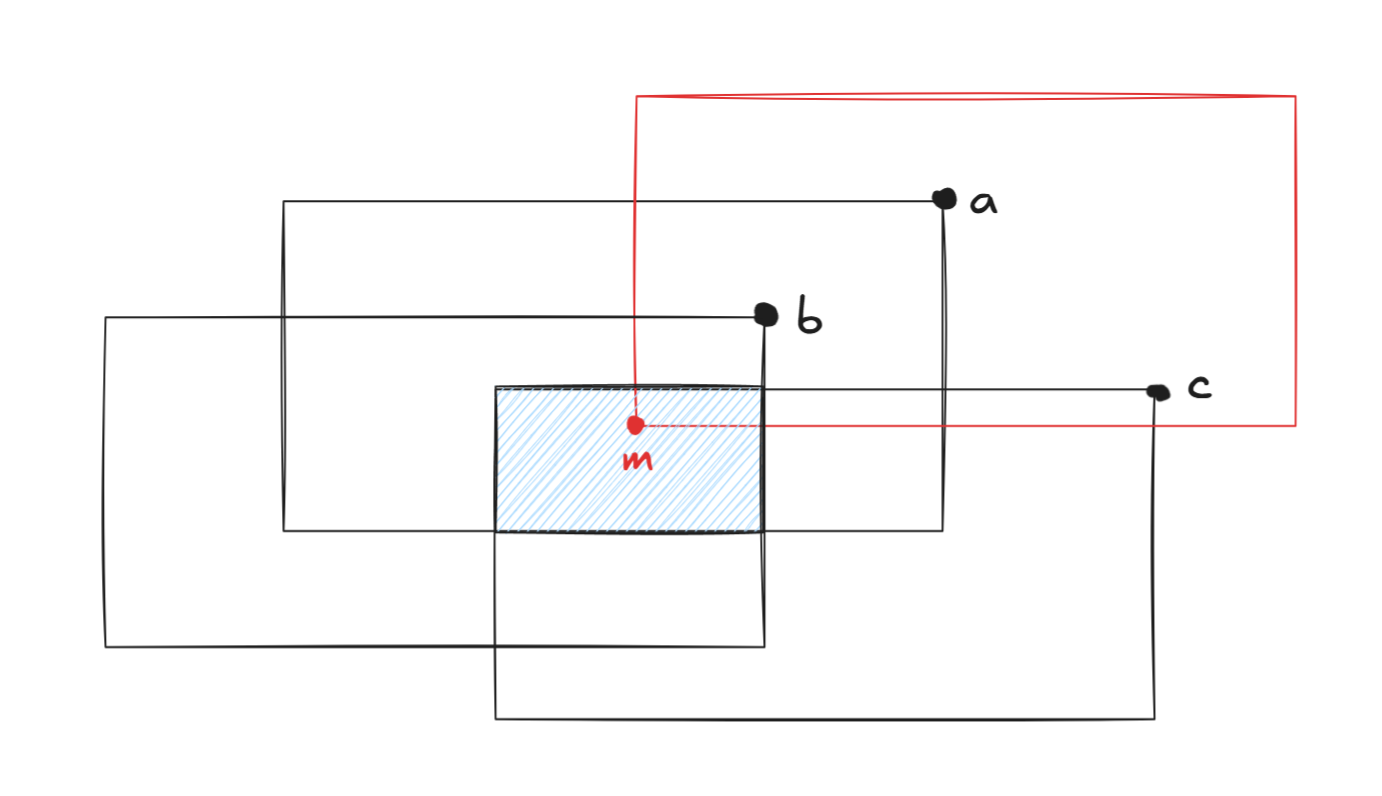
假设红框是当前的矩形，长宽固定；$a,b,c$为平面内的三个点，现在考虑能够将三个点都选中的区域在哪

过三个点都向左下作与红框大小一致的矩形，三个矩形的交集（蓝色区域）记为$M$，点$m\in M$，则以$m$点为左下角的红框都必定可以框住$a,b,c$三个点

因此数点问题转换为了染色问题！

在确定了一个矩形选取的形状之后，可以让每个平面内的点都给其左下角的矩形区域进行$+1$操作，最后整个平面内哪个点的值最大，其值就是能够框住的点的数量的最大值

如何快速实现二维染色呢 ？
可以通过差分标记+线段树维护扫描线来实现：

• 线段树维护扫描线上的区间最大值，同时需要区间修改功能
• 假设扫描线为平行于$y$轴的直线，从左到右扫描
• 遇到一个矩形的入边，在扫描线上区间加
• 遇到一个矩形的出边，在扫描线上区间减
• 每处理完一个横坐标，就调用$sum[root]$获取扫描线的线段树根节点所维护的最大值，更新全局最大值

但刚刚说的全都是建立在矩形形状确定的条件下
因此我们还需要解决矩形形状的问题：

$n$最大为$1e5$，那么可以枚举矩形长$x$，则宽$y=\lfloor \frac{k}{x}\rfloor$，在保证矩形面积尽可能大的同时不遗漏情况
$x\times x\le k$作为循环条件，则$x\le \sqrt{k}$，$k$与$n$为同一量级，所以枚举次数为$1e2.5=1e2\times \sqrt{10}=3e2$
对于一个确定的矩形形状，扫描线+线段树的复杂度为$n\log n=1e6$，$T$组数为$1e2$，总复杂度为$3e10$，在$8s$的限制下可以通过

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<unordered_set>
#include<string.h>
using namespace std;
using ll = long long;
#define int ll
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define ls p<<1
#define rs p<<1|1
#define mid ((l+r)>>1)
const int N = 1e4 + 5;
// int a[N][N];struct no {int x, y, w;
};
struct q {int down, up, val;
};
struct L {vector<q>query;
}line[N];int ma[N << 2], tag[N << 2];void pushup(int p) {ma[p] = max(ma[ls], ma[rs]);
}void pushdown(int p) {if (!tag[p]) return;tag[ls] += tag[p]; ma[ls] += tag[p];tag[rs] += tag[p]; ma[rs] += tag[p];tag[p] = 0;
}void modify(int p, int l, int r, int x, int y, int val) {if (x <= l && r <= y) { ma[p] += val; tag[p] += val; return; }pushdown(p);if (x <= mid)modify(ls, l, mid, x, y, val);if (y > mid)modify(rs, mid + 1, r, x, y, val);pushup(p);
}void build(int p, int l, int r) {ma[p] = tag[p] = 0;if (l == r)return;build(ls, l, mid), build(rs, mid + 1, r);
}void init(int X, int Y) {rep(i, 0, X + 1) {line[i].query.clear();}build(1, 1, Y);
}void eachT() {int n, k; cin >> n >> k;vector<no>node(n + 1);int X = 0, Y = 0;rep(i, 1, n) {int x, y, v; cin >> x >> y >> v;node[i] = { x,y,v };X = max(X, x), Y = max(Y, y);}int ans = 0;for (int p = 1; p * p <= k; p++) {int y = k / p, x = p;rep(t, 1, 2) {swap(x, y);init(X, Y);rep(i, 1, n) {int x0 = node[i].x, y0 = node[i].y, w = node[i].w;line[max(x0 - x + 1, 1ll)].query.push_back({ max(y0 - y + 1,1ll),y0,w });line[x0 + 1].query.push_back({ max(y0 - y + 1,1ll),y0,-w });}rep(i, 1, X) {for (auto& ele : line[i].query) {int down = ele.down, up = ele.up, val = ele.val;modify(1, 1, Y, down, up, val);}int cmp = ma[1];ans = max(ans, cmp);}}}cout << ans << '\n';
}
signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1;cin >> t;while (t--)eachT();
}