【C++高阶五】mapset对红黑树的封装
【C++高阶五】map&set对红黑树的封装
- 1.将红黑树封装为泛型
- 2.泛型红黑树的修改和Find接口
- 3.迭代器
- 4.insert接口
- 5.map的operator[]接口
- 6.总代码展示
C++的STL库中把红黑树封装为了两个容器map与set
本博客将基于红黑树来实现map和set的封装
如果不了解红黑树,可见博客【C++高阶四】红黑树
1.将红黑树封装为泛型
我们现有的红黑树结构如下:
enum color//颜色枚举
{RED,BLACK
};template<class K, class V>
struct RBTreeNode//红黑树节点结构体
{RBTreeNode<K, V>* _left;//左指针RBTreeNode<K, V>* _right;//右指针RBTreeNode<K, V>* _parent;//父亲指针color _color;//颜色标记位pair<K, V> _kv;//KV值RBTreeNode(const pair<K, V>& KV)//初始化列表构造:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(KV), _color(RED){}
};template<class K, class V>
class RBTree//红黑树
{typedef RBTreeNode<K, V> Node;//定义节点为Node
public:private:Node* _root = nullptr;
};
这颗红黑树有一个问题,它的节点,存储的值是pair<K, V> _kv,是以键值对的形式来存储数据。但是在STL中,set只是存储key值的,只有map才存储键值对。如果我们要让红黑树可以同时作为map和set的底层,那么我们就要让这个红黑树的节点可以存储更多种类型的数据,所以要让节点RBTreeNode内部存储泛型:
template<class T>
struct RBTreeNode//红黑树节点结构体
{RBTreeNode<T>* _left;//左指针RBTreeNode<T>* _right;//右指针RBTreeNode<T>* _parent;//父亲指针color _color;//颜色标记位T _data;//data值RBTreeNode(const T& data)//初始化列表构造:_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(RED){}
};把原先的模板template<class K, class V>换成了template<class T>,并把pair<K, V> _kv;改为了T _data
当我们需要存储键值对,那么T就是pair<K, V>
当我们只存储key值,那么T就是K
相应的,我们的RBTree本体也要修改一下:
template<class T>
class RBTree//红黑树
{typedef RBTreeNode<T> Node;//定义节点为Node
public:private:Node* _root = nullptr;
};
现在尝试封装红黑树,写出map和set的基本框架:
my_set.h:
template<calss K>
class set
{
public:private:RBTree<K> _tree;
}
my_map.h:
template<class K,class V>
class map
{
public:
private:RBTree<pair<K,V>> _tree;
}
经过这一层封装,我们的map和set的基本框架就有了
但是有一个小问题:map和set中的key值是不可以修改的,所以我们要给K的类型加上const修饰,不过要注意map中的value是可以修改的,所以不是给pair加上const修饰,而是只修饰K
my_set.h:
template<calss K>
class set
{
public:private:RBTree<const K> _tree;
}
my_map.h:
template<class K,class V>
class map
{
public:
private:RBTree<pair<const K,V>> _tree;
}
2.泛型红黑树的修改和Find接口
原本红黑树的Find接口:
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if(cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;
}
- 第一个问题:我们已经把模板从
template<class K, class V>换成了template<class T>,现在已经没有K这个类型了,意味着我们在给Find传参的时候,不可以直接传const K& key
但我们在红黑树中查找一定是需要key的,所以我们要在模板参数中加一个K,也就是template<class K, class T>,前面的K用于传入key的类型,后面的T用于传入红黑树存储的数据类型
所以修改后的泛型红黑树框架如下:
template<class K ,class T>
class RBTree//红黑树
{typedef RBTreeNode<T> Node;//定义节点为Node
public:private:Node* _root = nullptr;
};
- 第二个问题:我们对红黑树的节点类
RBTreeNode改造后,其内部存储的已经不是_kv了,而是_data,对于set而言,这个_data是没有first这个成员的,因此我们不能直接通过_kv.first这种方式来访问key;但是对于map而言,这个key还是_data中的成员变量first。也就是map和set取用key值的方式不同,我们无法统一处理
为了用统一的方式从_data中获得 map和set 各自的key,我们在红黑树的外部写仿函数,然后在仿函数的内部返回key值
所以给红黑树传入第三个模板参数KeyOfT:
template<class K ,class T,class KeyOfT>//KeyOfT是仿函数,用于得到T类对象中的key
class RBTree//红黑树
{typedef RBTreeNode<T> Node;//定义节点为Node
public:private:Node* _root = nullptr;
};
修改完红黑树后,要分别给set和map类添加仿函数:
set:
template<calss K>
class set
{
public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};
private:RBTree<K,K, SetKeyOfT> _tree;
}
map:
template<class K,class V>
class map
{
public:struct MapKeyOfT{const K& operator()(const pair<K,V>& kv){return kv.first;}};
private:RBTree<K,pair<const K, V>, MapKeyOfT> _tree;
}
再对Find函数进行改造:
bool Find(const K& key)
{KeyOfT kot;Node* cur = _root;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if(kot(cur->_data) > key){cur = cur->_left;}else{return true;}}return false;
}
3.迭代器
先搭建出迭代器iterator的基本框架:
template<class T,class Ptr,class Ref>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T,Ptr,Ref> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}
};
中序遍历可以通过递归按照“左子树 - 根 - 右子树”的顺序遍历,但迭代器该如何移动?
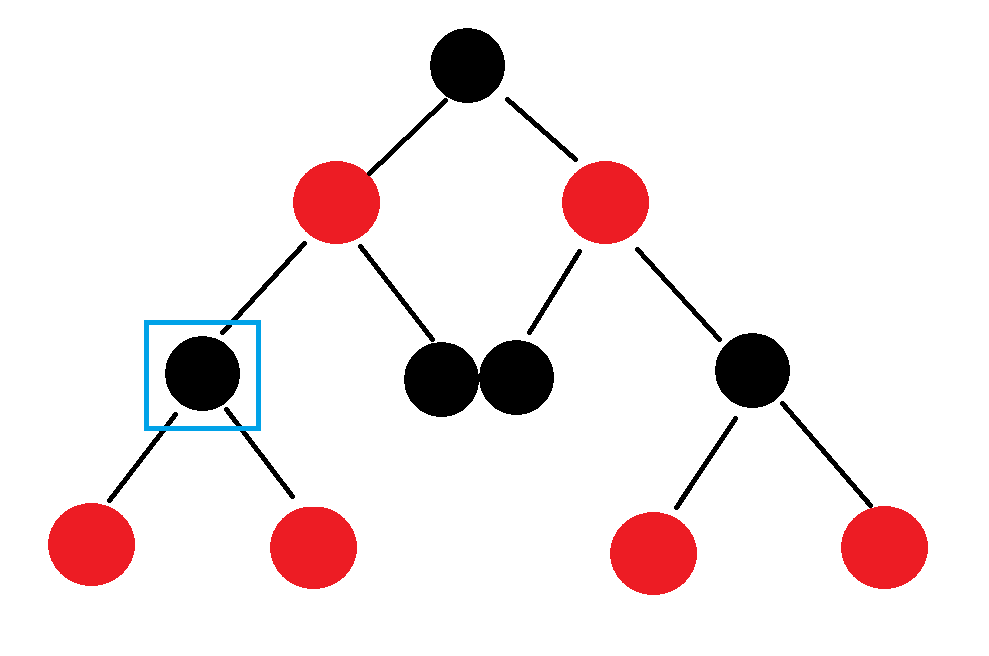
当迭代器指向蓝色方框位置时,说明迭代器就遍历到了这里,说明左子树已经遍历完成,遍历蓝色方框(根)后就要遍历右子树(找到右子树的最左节点)
蓝色方框移动:
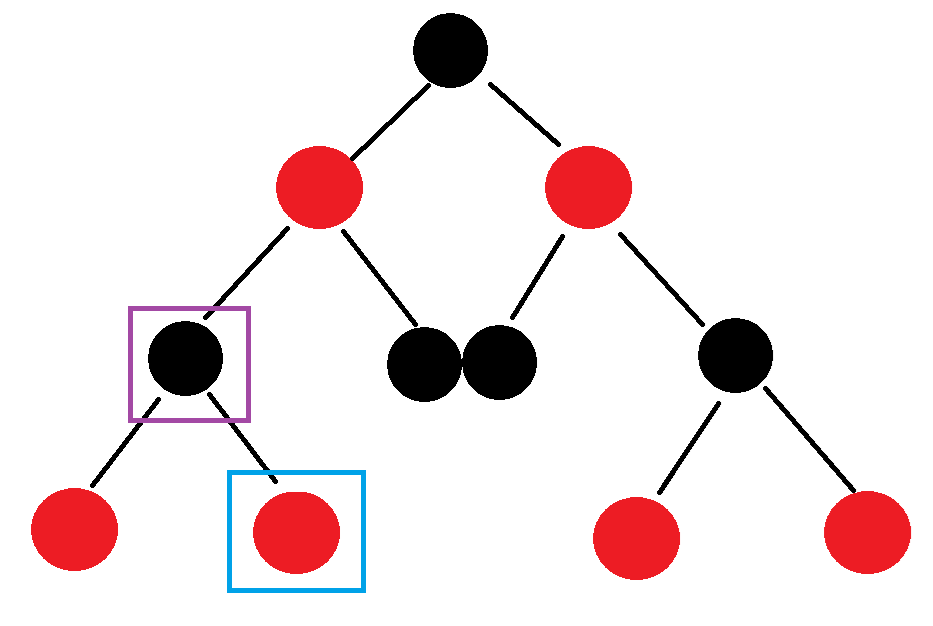
当迭代器指向蓝色方框位置时,右子树为空,说明以蓝色框为根的整颗子树都遍历完毕了,也说明以紫色框为根的整颗子树都遍历完毕了(中序遍历,根节点一定在右子树前遍历完),那么我们就要向上移动蓝色方框,直到蓝色方框是其父节点的左子树时,将蓝色方框向上移动给其父节点
蓝色方框移动:
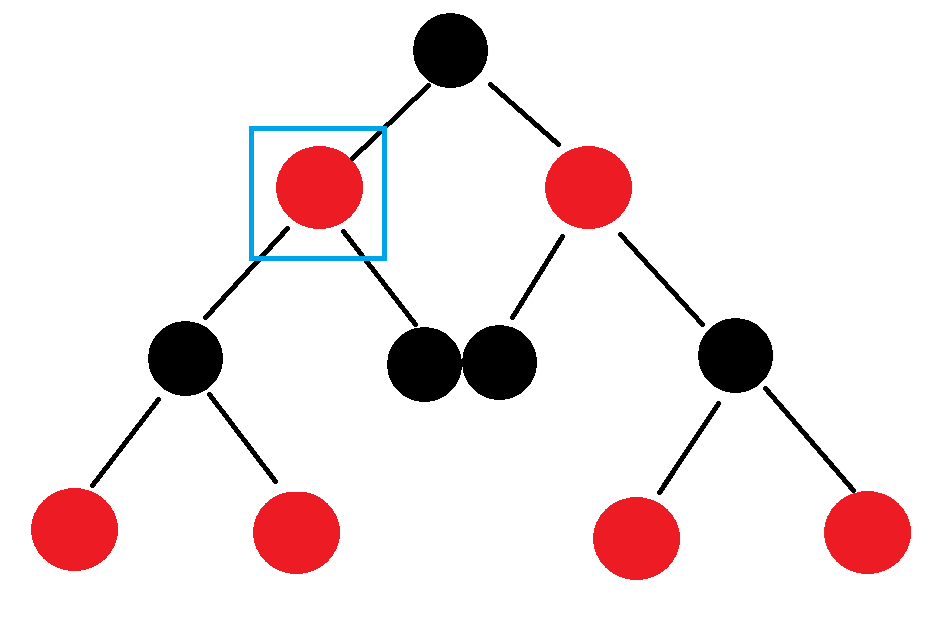
- 如果迭代器当前节点的右子树不为空,遍历右子树(找到右子树的最左节点)
- 如果迭代器当前节点的右子树为空,向上找第一个满足条件的节点:该节点其左子树是自己的前一个节点
代码如下:
Self& operator++()
{if (_node->_right){Node* cur = _node->_right;while (cur->left){cur = cur->_left;}_node = cur;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}_node = parent;}return *this;
}
operator–同理,只是规律相反:
- 如果迭代器当前节点的左子树不为空,遍历左子树(找到左子树的最右节点)
- 如果迭代器当前节点的左子树为空,向上找第一个满足条件的节点:该节点的右子树是自己的前一个节点
Self& operator--()
{if (_node->_left){Node* cur = _node->_left;while (cur->right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;
}
接下来我们要把迭代器的类封装进RBTree中,首先在RBTree中定义出iterator和const_iterator:
typedef RBTreeIterator<T, T*, T&> iterator;
typedef RBTreeIterator<T, const T*, const T&> const_iterator;
接着写出begin,end的iterator接口:
iterator begin()//中序遍历的第一个节点是整棵树的最左侧节点
{Node* cur = _root;while (cur->_left){cur = cur->_left;}return iterator(cur);
}iterator end()
{return iterator(nullptr);
}
const_iterator的begin和end同理:
const_iterator begin()const
{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);
}const_iterator end()const
{return const_iterator(nullptr);
}
我们再封装出map和set的迭代器,直接复用RBTree的迭代器接口即可:
mySet.h:
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin()
{return _tree.begin();
}iterator end()
{return _tree.end();
}const_iterator begin()const
{return _tree.begin();
}const_iterator end()const
{return _tree.end();
}
myMap.h:
typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::const_iterator const_iterator;iterator begin()
{return _tree.begin();
}iterator end()
{return _tree.end();
}const_iterator begin()const
{return _tree.begin();
}const_iterator end()const
{return _tree.end();
}
在
typedef的时候,由于RBTree是一个模板,我们到模板的域中访问了变量,而编译器无法区分模板中const_iterator的是变量还是类型,所以编译器会默认把它视为一个变量。如果它是一个类型,那么我们要明确告诉编译器,即通过typename关键词,否则const_iterator会被识别为一个变量,而不是一个类型
由于STL中,find接口返回的是迭代器,所以我们还要把find的返回值改为迭代器,而不是使用布尔值返回
iterator Find(const K& key)
{KeyOfT kot;Node* cur = _root;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return iterator(cur);}}return end();
}
4.insert接口
在map和set中,insert的返回值比较特殊,其会返回
pair<iterator, bool>
- 如果插入值data原先存在,此时iterator指向原先的data节点,bool值返回false表示插入失败
- 如果插入值data原先不存在,此时iterator指向新插入的data节点,bool值返回true表示插入成功
RBTree:
pair<Node*,bool> Insert(const T& data)
{if (_root == nullptr){_root = new Node(data);_root->_color = BLACK;//根节点是黑的return make_pair(_root,true);}Node* cur = _root;Node* parent = nullptr;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data))//向右走{parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data))//向左走{parent = cur;cur = cur->_left;}else{return make_pair(cur, false);//相等就插入失败}}cur = new Node(data);Node* newnode = cur;//cur会不停变动,但最后返回的是新插入的那个节点//链接if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}//此时new出来的节点的parent还指向空cur->_parent = parent;//新插入节点的父亲 存在 且是 红色,再调整while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//新插入的节点其父节点在子树左侧{Node* uncle = grandfather->_right;if (uncle && uncle->_color == RED)//uncle存在且为红{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在 或uncle是黑色{if (cur = parent->left)//grandfather和parent和cur是线性{RotateR(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateL(parent);RotateR(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求,跳出循环}}else//新插入的节点其父节点在子树右侧{Node* uncle = grandfather->_left;if (uncle && uncle->_color == RED)//uncle 存在 且为 红色{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle 不存在 或为 黑色{if (cur = parent->right)//grandfather和parent和cur是线性{RotateL(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateR(parent);RotateL(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求,跳出循环}}}_root->color = BLACK;return make_pair(newnode,true);
}
map:
pair<Node*, bool> insert(const pair<K, V>& kv)
{return _tree.Insert(kv);
}
set:
pair<Node*, bool> insert(const K& key)
{return _tree.Insert(key);
}
5.map的operator[]接口
map还重载了[],这个重载比较复杂,但是非常有用,其声明:
V& operator[] (const K& key);
作用:接受一个key值,然后返回这个key对应的value的引用
等价于下列代码:
(*((this->insert(make_pair(key,V()))).first)).second
我们将以上代码拆解为四个部分解读
第一部分:
make_pair(key, V( ))
这是在利用参数k,通过
make_pair()构造一个pair,这个pair的value使用了V( )(V就是value的类型)来调用默认构造,最后就得到了一个pair<key, value>
第二层:
this->insert( )
上一层我们构造了一个
pair<key, value>,然后它作为参数传入到这个insert()中,相当于把刚刚构造的节点插入进map中。map的插入后,不论成功与否,都会返回一个pair<Node*, bool>,Node*用于指向key,bool用于标识插入是否成功。所以这一层最后得到了一个pair,分别存储了指向key的指针和bool值
第三层:
( ).first
上一层中我们得到了
pair<Node*, bool>,这一层访问它的first,也就是访问了Node*,所以这一层得到了指向key值的地址
第四层:
(*( )).second
上一层拿到了指向key的地址,这一层先对地址解引用
*( ),此时就得到了一个map的节点。而map的节点是pair<key, value>,所以我们解引用得到了一个pair,随后通过( ).second访问pair<key, value>的second,也就是value。最后返回这个value的引用
operator[]实现:
V& operator[](const K& key)
{pair<Node*,bool>& ret = insert(make_pair(key, V()));return ret.first->second;
}
operator[ ]的作用:
- 插入一个
key值:
dict["left"];
以上语句在dict中插入了一个key = "left"的节点,尽管其没有value- 插入一对
key - value:
dict["left"] = "左边";
由于operator[ ]返回的是对应的引用,因此我们可以直接給返回值赋值,此时我们就插入了一个节点key = "left",value = "左边"- 修改
key对应的value:
dict[“coffe”] = "咖啡";
如果我们的dict原先就存在key = "coffe"的节点,以上代码可以修改这个key的value值- 得到
key对应的value:
cout << dict["coffe"] << endl;
由于我们拿到的是value的引用,我们也可以把它作为一个值赋值给别人或者输出
由于我们拿到的是value的引用,我们也可以把它作为一个值赋值给别人或者输出
6.总代码展示
RBTree.h:
enum color//颜色枚举
{RED,BLACK
};template<class T>
struct RBTreeNode//红黑树节点结构体
{RBTreeNode<T>* _left;//左指针RBTreeNode<T>* _right;//右指针RBTreeNode<T>* _parent;//父亲指针color _color;//颜色标记位T _data;//data值RBTreeNode(const T& data)//初始化列表构造:_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(RED){}
};template<class T, class Ptr, class Ref>
struct RBTreeIterator//红黑树迭代器
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ptr, Ref> Self;RBTreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator++(){if (_node->_right){Node* cur = _node->_right;while (cur->left){cur = cur->_left;}_node = cur;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}Self& operator--(){if (_node->_left){Node* cur = _node->_left;while (cur->right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}public:Node* _node;
};//set->RBTree<K,K,SetKeyOfT> _tree;
//map->RBTree<K,pair<const K,T>,MapKeyOfT> _tree;
template<class K, class T,class KeyOfT>
class RBTree//红黑树
{typedef RBTreeNode<T> Node;//定义节点为Node
public:typedef RBTreeIterator<T, T*, T&> iterator;typedef RBTreeIterator<T, const T*, const T&> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin()const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end()const{return const_iterator(nullptr);}pair<Node*,bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_color = BLACK;//根节点是黑的return make_pair(_root,true);}Node* cur = _root;Node* parent = nullptr;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data))//向右走{parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data))//向左走{parent = cur;cur = cur->_left;}else{return make_pair(cur, false);//相等就插入失败}}cur = new Node(data);Node* newnode = cur;//cur会不停变动,但最后返回的是新插入的那个节点//链接if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}//此时new出来的节点的parent还指向空cur->_parent = parent;//新插入节点的父亲 存在 且是 红色,再调整while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//新插入的节点其父节点在子树左侧{Node* uncle = grandfather->_right;if (uncle && uncle->_color == RED)//uncle存在且为红{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在 或uncle是黑色{if (cur = parent->left)//grandfather和parent和cur是线性{RotateR(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateL(parent);RotateR(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求,跳出循环}}else//新插入的节点其父节点在子树右侧{Node* uncle = grandfather->_left;if (uncle && uncle->_color == RED)//uncle 存在 且为 红色{uncle->_color = parent->_color = BLACK;grandfather->color = RED;cur = grandfather;parent = cur->_parent;}else//uncle 不存在 或为 黑色{if (cur = parent->right)//grandfather和parent和cur是线性{RotateL(grandfather);grandfather->color = RED;parent->color = BLACK;}else//grandfather和parent和cur是折线型{RotateR(parent);RotateL(grandfather);cur->color = BLACK;grandfather->_color = RED;}break;//旋转后一定满足要求,跳出循环}}}_root->color = BLACK;return make_pair(newnode,true);}void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_ + left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* parentparent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parentparent->_left = parent){parentparent->_left = subR;}else{parentparent->_right = subR;}subR->_parent = parentparent;}subR->_bf = parent->_bf = 0;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}iterator Find(const K& key){KeyOfT kot;Node* cur = _root;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return iterator(cur);}}return end();}
private:Node* _root = nullptr;
};
my_set.h:
#include "RBTree.h"namespace lhc
{template<class K>class set{public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin(){return _tree.begin();}iterator end(){return _tree.end();}const_iterator begin()const{return _tree.begin();}const_iterator end()const{return _tree.end();}pair<Node*, bool> insert(const K& key){return _tree.Insert(key);}private:RBTree<K,K, SetKeyOfT> _tree;};
}
my_map.h:
#include "RBTree.h"namespace lhc
{template<class K, class V>class map{public:struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _tree.begin();}iterator end(){return _tree.end();}const_iterator begin()const{return _tree.begin();}const_iterator end()const{return _tree.end();}V& operator[](const K& key){pair<Node*, bool>& ret = insert(make_pair(key, V()));return ret.first->second;}pair<Node*, bool> insert(const pair<K, V>& kv){return _tree.Insert(kv);}private:RBTree<K,pair<const K, V>, MapKeyOfT> _tree;};
}
