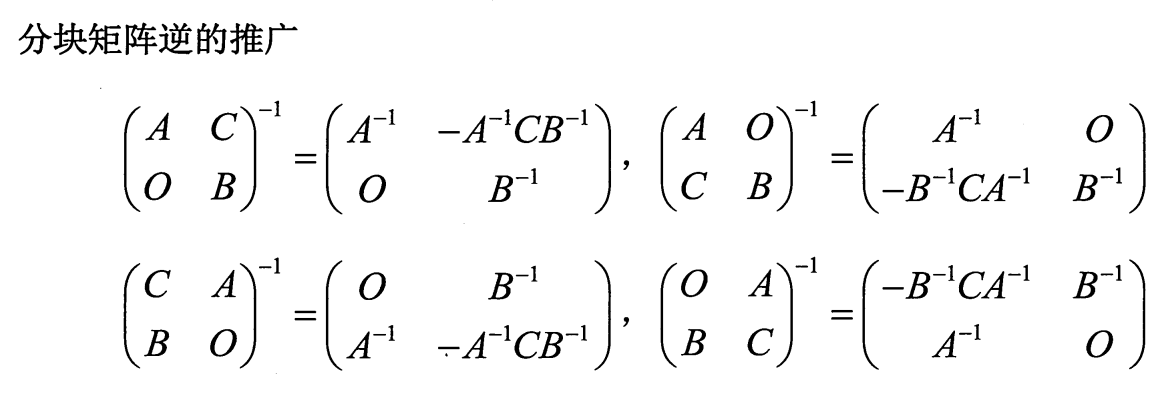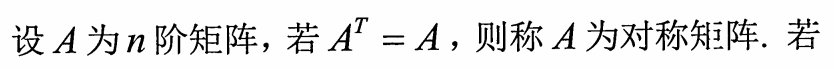第二章 矩阵
专题一 矩阵的基本运算
1.矩阵的定义
由mxn个数构成的m行n列的数表

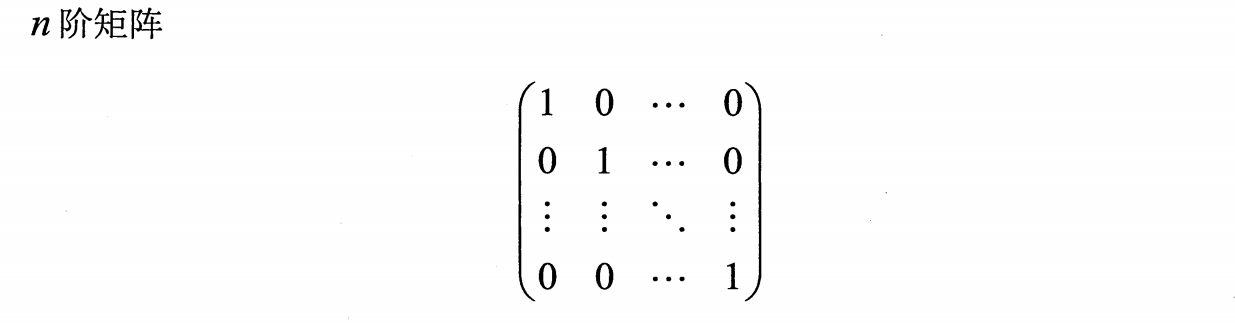
称为单位矩阵,记作E.
若矩阵A与B有相同的行数和相同的列数,则称A,B为同型矩阵
2.矩阵加法的定义
设、
是同型矩阵(行列数分别相同 ),则
与
的和是一个新矩阵,其元素为对应位置元素相加,即
,记作
。
3.矩阵数乘的定义
设矩阵,
是常数,将矩阵
的每个元素都乘以k 得到新矩阵
,这个新矩阵就是
与
的数乘,记作
。
4.矩阵乘法的定义

一行乘一列,对应行列数字相乘再相加。C行列=(行×列)

因式分解的公式对矩阵不适用
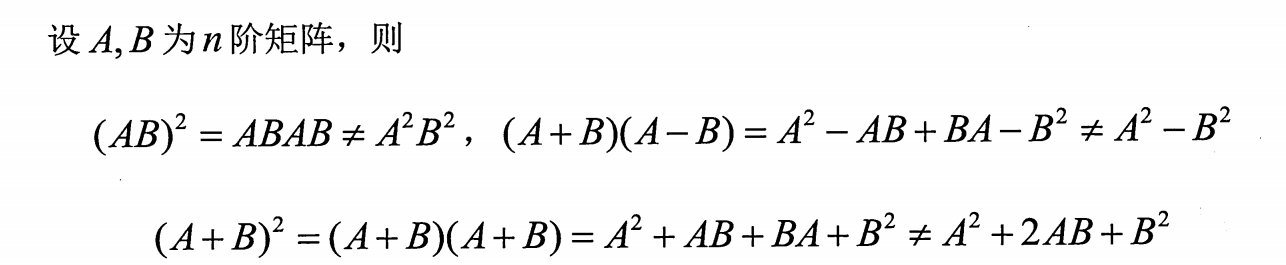
特别地,当时,
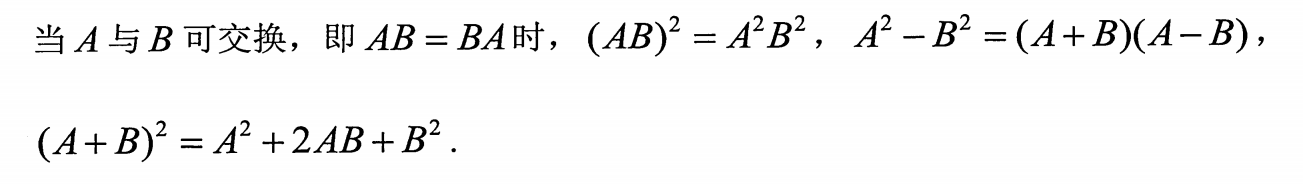


(1)pr:AB=AC,左乘,得B=C
(2)pr:由AB=AC,得A(B-C)=0,
由阶矩阵
,得
,故
,即
5.转置的定义
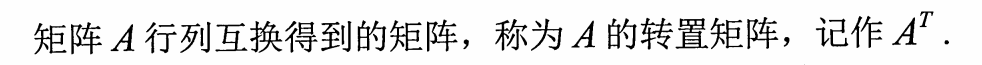
6.对称矩阵与反对称矩阵的定义

7.转置的性质
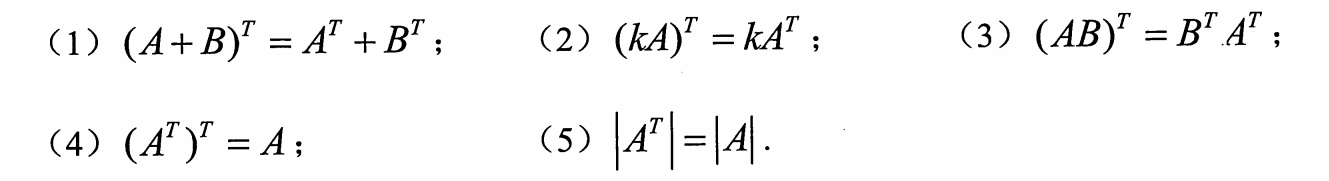
专题二 矩阵的逆
1.逆的定义
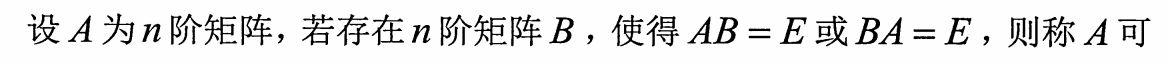
![]()
2.逆的性质
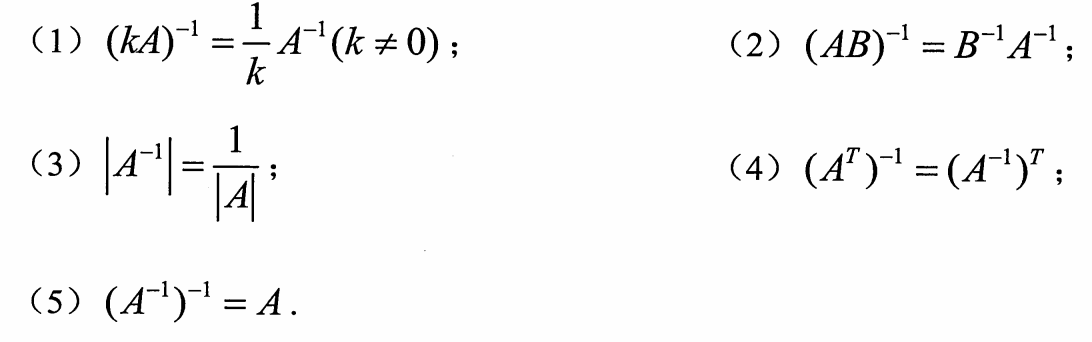
3.可逆的充要条件

4.逆的求法
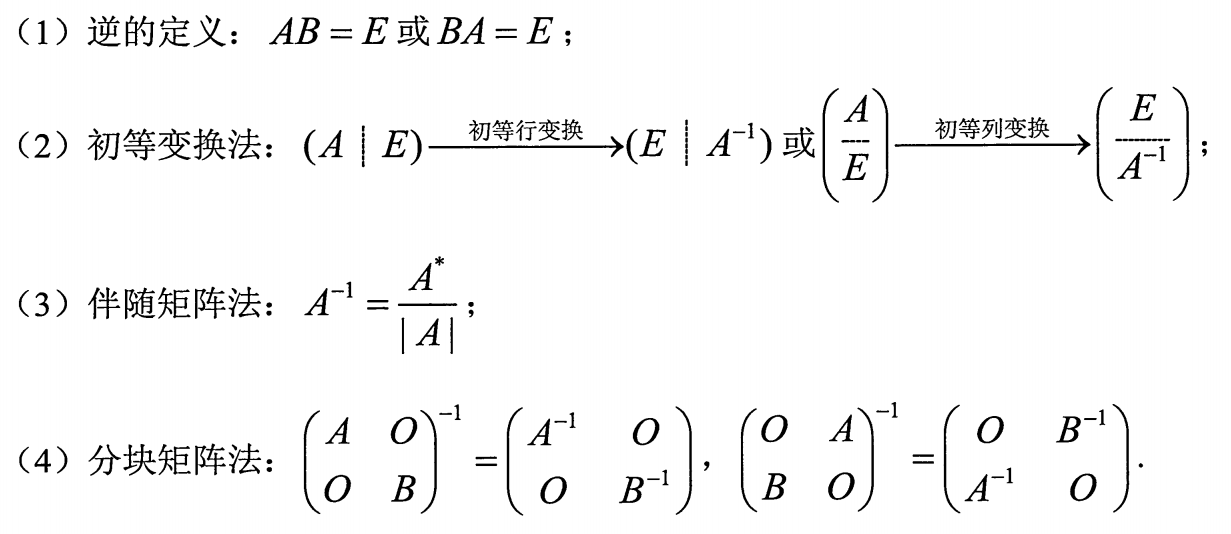
专题三 矩阵的秩
1.k阶子式的定义
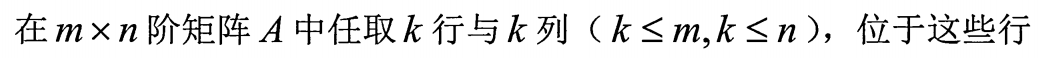
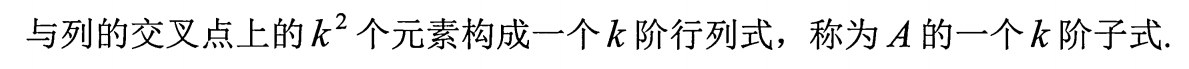
2.秩的定义
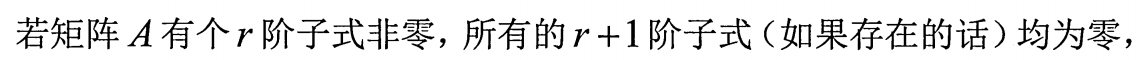
![]()

3.满秩的定义
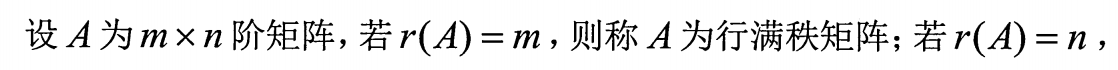
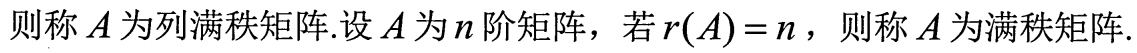
4.秩的性质
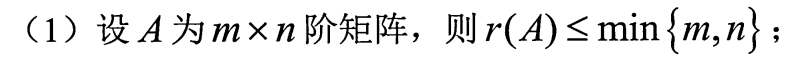
秩小于等于行数和列数
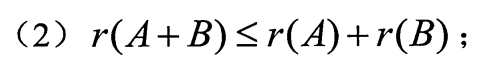
和差的秩小于等于秩的和
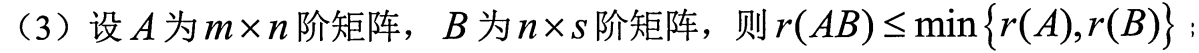
乘积的秩小于等于每一个
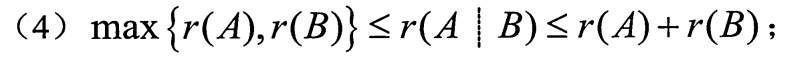
联立的秩大于等于每一个,小于等于秩的和
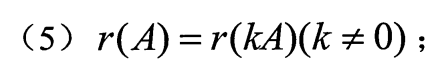
乘非零常数秩不变

乘可逆矩阵秩不变
pr:性质三,
,故
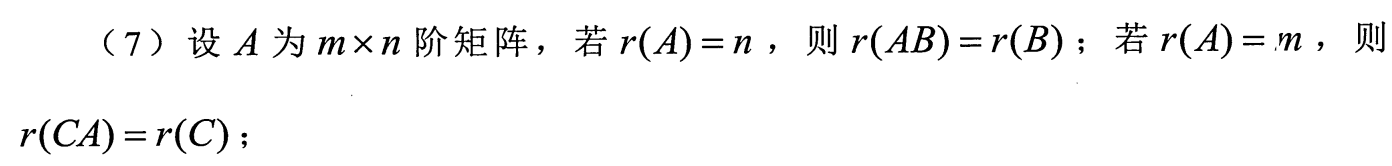
左乘列满秩或右乘行满秩,秩不变
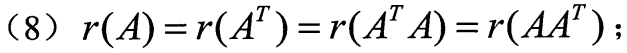
乘转置矩阵秩不变

乘积为0,秩的和小于等于n
5.秩的求法

行阶梯形:,每行第1个非0的数下面的元素均为0
专题四 伴随矩阵
1.伴随矩阵的定义
 注意这是转置的
注意这是转置的

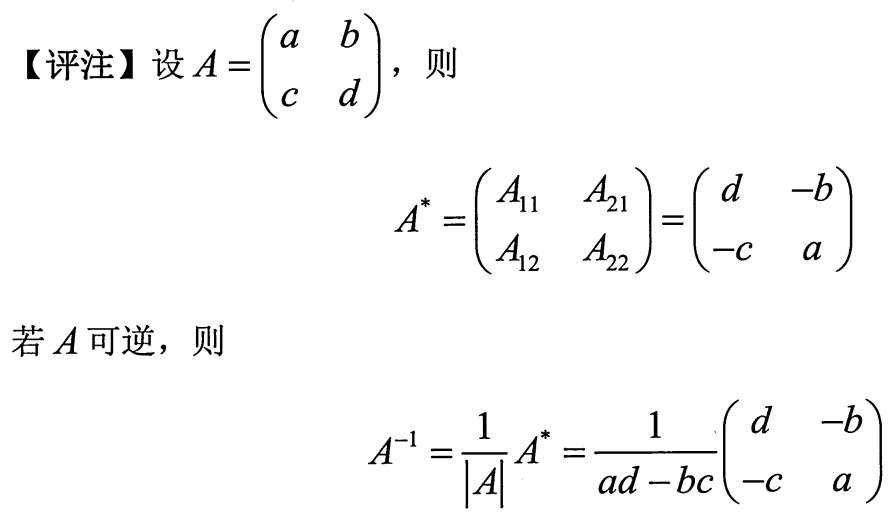
主对角互换,副对角变号
2.伴随矩阵的性质
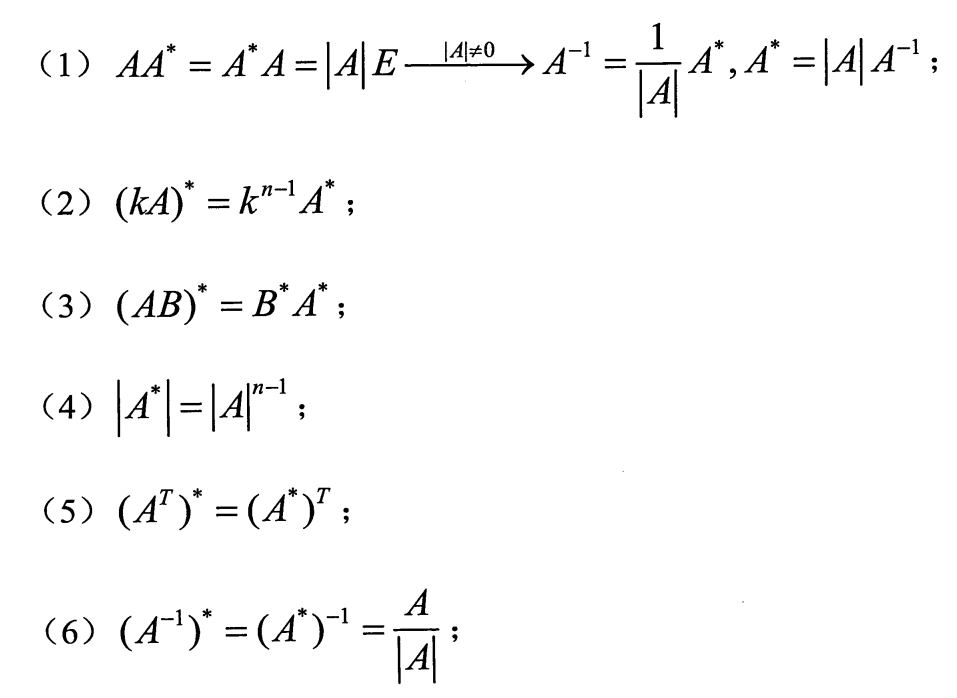
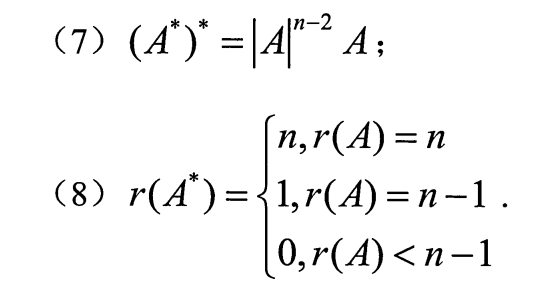

其他证明见课本
(1)引入伴随矩阵是为了满足展开定理
总结:
3个n-1次方:型
总结:
上标运算可交换:
n代表高次幂,||代表行列式
专题五 初等变换与初等矩阵
1.初等变换的定义

2.初等矩阵的定义
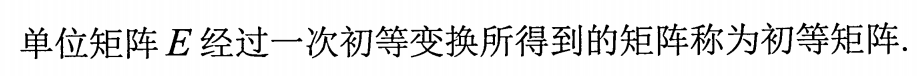

3.初等变换与初等矩阵的性质

证明见课本
4.初等变换与初等矩阵的应用

5.矩阵等价的定义
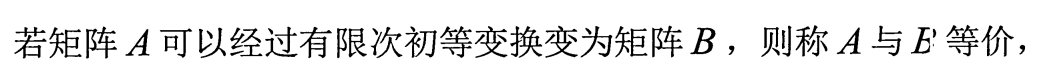
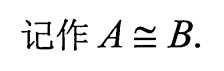
6.矩阵等价的充要条件

专题六 分块矩阵
1.分块矩阵的加法
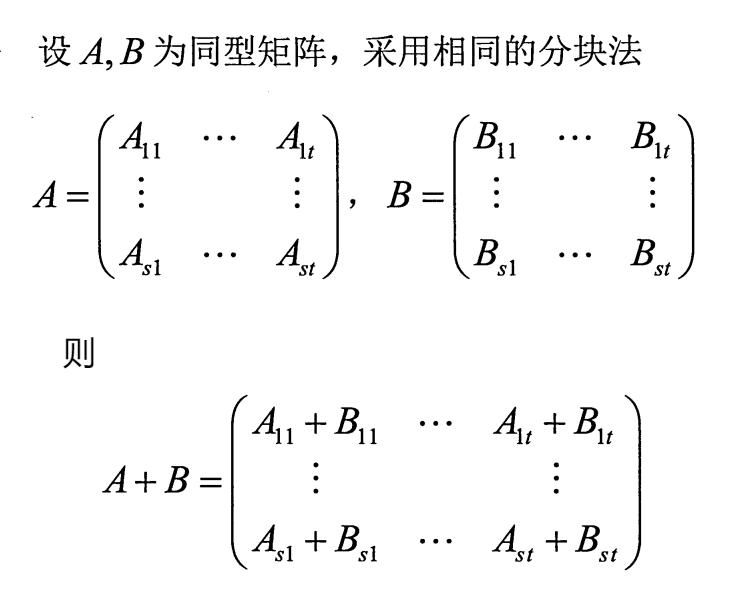
2.分块矩阵的数乘

3.分块矩阵的乘法
![]()
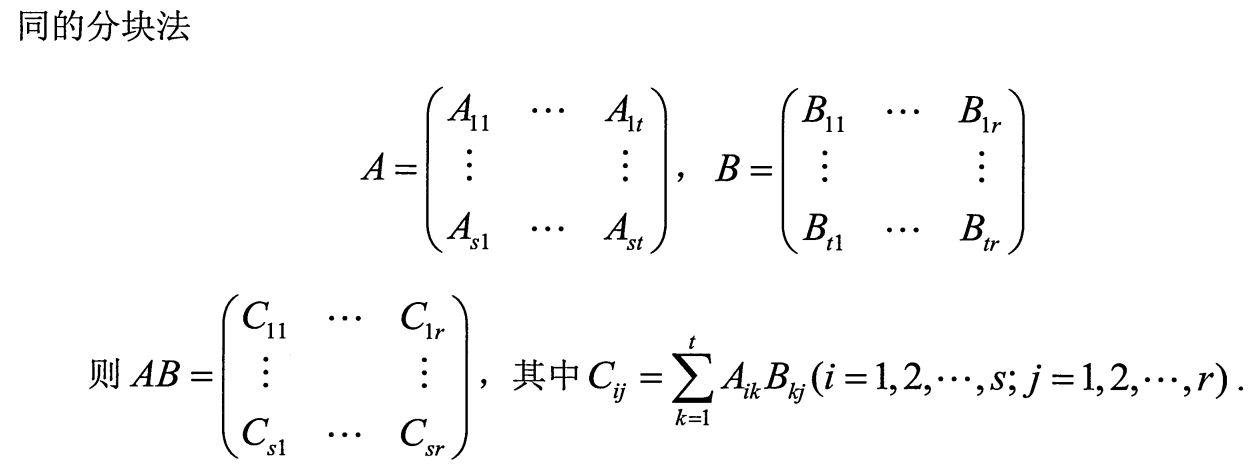
与矩阵乘法类似

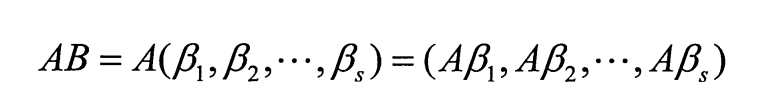
4.分块矩阵的转置
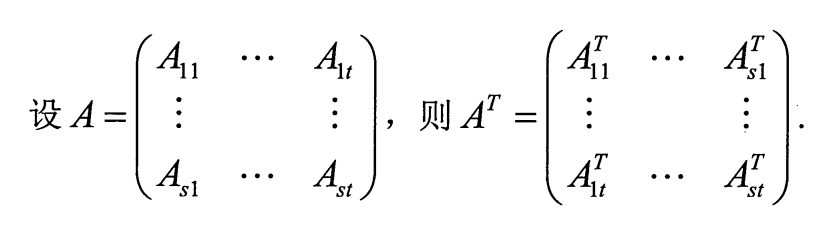
5.分块矩阵的逆