当前位置： 首页 > ops >正文

#Datawhale 组队学习#7月-强化学习Task6

ops 2025/8/3 12:50:51

本篇为强化学习的Task6，本次任务是：DDPG算法、PPO算法、SAC算法、阅读视觉强化学习／ICLR25Oral论文（可选）

前面的链接可以参考：
#Datawhale组队学习#7月-强化学习Task1-CSDN博客

#Datawhale组队学习#7月-强化学习Task2-CSDN博客

#Datawhale 组队学习#强化学习Task4-CSDN博客

#Datawhale 组队学习#强化学习Task5-CSDN博客

第十一章DDPG算法

11.1 DPG 方法

深度确定性策略梯度算法（DDPG），是一种确定性的策略梯度算法。在介绍DDPG算法之前，我们先了解一下DPG算法。

DQN算法的一个主要缺点就是不能用于连续动作空间，而要想适配连续动作空间，我们干脆就将选择动作的过程变成一个直接从状态映射到具体动作的函数，这样一来就把求解Q函数、贪心选择动作这两个过程合并成了一个函数，也就是我们常说的Actor。相当于是把 ε—greedy策略函数部分换成了Actor。

11.2 DDPG 算法

 在DPG算法 的基础上，再结合一些技巧，就是DDPG算法了，这些技巧既包括DQN算法中也用到的目标网络、经验回放等，也包括引入噪声来增加策略的探索性。

关键技术

  • 目标网络：稳定训练，软更新

  • 经验回放：打破数据相关性

  • 探索噪声：OU噪声 （物理系统）或高斯噪声

11.3 DDPG 算法的优缺点

总的来说，DDPG算法的优点主要有：

  • 适用于连续动作空间：DDPG算法采用了确定性策略来选择动作，这使得它能够直接处理连续动作空间的问题。
  • 高效的梯度优化：DDPG算法使用策略梯度方法进行优化，其梯度更新相对高效，并且能够处理高维度的状态空间和动作空间。同时，通过Actor-Critic结构，算法可以利用值函数来辅助策略的优化，提高算法的收敛速度和稳定性。
  • 经验回放和目标网络：经验回放机制可以减少样本之间的相关性，提高样本的有效利用率，并且增加训练的稳定性。目标网络可以稳定训练过程，避免值函数估计和目标值之间的相关性问题，从而提高算法的稳定性和收敛性。

 而缺点在于：

  • 只适用于连续动作空间：这既是优点，也是缺点。

  • 高度依赖超参数：DDPG算法中有许多超参数需要进行调整，除了一些DQN的算法参数例如学习率、批量大小、目标网络的更新频率等，还需要调整一些OU噪声的参数 调整这些超参数并找到最优的取值通常是一个挑战性的任务，可能需要大量的实验和经验。

  • 高度敏感的初始条件：DDPG算法对初始条件非常敏感。初始策略和值函数的参数设置可能会影响算法的收敛性和性能，需要仔细选择和调整。

  • 容易陷入局部最优：由于采用了确定性策略，可能会导致算法陷入局部最优，难以找到全局最优策略。为了增加探索性，需要采取一些措施，如加入噪声策略或使用其他的探索方法。

11.4 TD3 算法

TD3算法，英文全称twin delayed DDPG，翻译过来就是双延迟确定性策略梯度算法。相对于DDPG算法， 算法的改进主要做了三点重要的改进，一是 双Q网络，二是 延迟更新，三是躁声正则。

双Q网络的思想其实很简单，就是在DDPG算法中的Critic网络上再加一层，这样就形成了两个Critic网络。这跟Double DQN的原理本质上是一样的，这样做的好处是可以减少Q值的过估计，从而提高算法的稳定性和收敛性。

延迟更新更像是一种实验技巧，即在训练中Actor的更新频率要低于Critic的更新频率。

躁声正则即目标策略平滑正则化。

11.5 实战：DDPG 算法

DDPG伪代码如下：

 DDPG实现技巧：

# 1. OU噪声类（Pendulum环境适用）
class OUNoise:def __init__(self, size, mu=0.0, theta=0.15, sigma=0.2):self.state = np.ones(size) * mudef sample(self):dx = self.theta * (self.mu - self.state) + self.sigma * np.random.randn(len(self.state))self.state += dxreturn self.state# 2. Critic网络设计（状态与动作早期融合）
class Critic(nn.Module):def forward(self, state, action):x = torch.cat([state, action], 1)  # 关键：先拼接再输入！x = F.relu(self.fc1(x))return self.fc2(x)

11.6 实战：TD3 算法

TD3代码核心差异：

# 双Critic计算目标Q值
target_actions = actor_target(next_states)
target_noise = torch.clamp(torch.randn_like(target_actions) * 0.2, -0.5, 0.5)
target_actions = (target_actions + target_noise).clamp(env.action_space.low, env.action_space.high)# 取两个Critic目标网络的最小值
target_Q1 = critic_target1(next_states, target_actions)
target_Q2 = critic_target2(next_states, target_actions)
target_Q = torch.min(target_Q1, target_Q2)

调参建议

参数DDPG推荐值TD3推荐值作用
学习率 (Actor)1e-4 ~ 1e-33e-4 ~ 1e-3策略网络更新速度
学习率 (Critic)1e-3 ~ 5e-31e-3 ~ 3e-3值网络更新速度
软更新系数 $\tau$0.005~0.010.005~0.01目标网络更新平滑度
噪声方差衰减线性衰减0.3→0.1固定截断噪声平衡探索与利用

11.7 习题

1. DDPG 算法是 off-policy 算法吗？为什么？
是的，DDPG 是 off-policy 算法。因为它通过经验回放机制存储和重用历史经验数据，这些数据由任意行为策略生成，与当前优化的策略无关，从而提升样本利用效率。

2. 软更新相比于硬更新的好处是什么？为什么不是所有的算法都用软更新？
软更新的优势在于平滑调整目标网络参数，避免硬更新导致的训练振荡，提升稳定性。但软更新并非通用，因为其收敛速度较慢，且在简单环境（如 DQN）中硬更新已足够高效。

3. 相比于 DDPG 算法，TD3 算法做了哪些改进？请简要归纳。
TD3 的三大核心改进：

  • 双 Critic 网络：取两个 Critic 的最小值作为目标 Q 值，抑制高估偏差；

  • 延迟 Actor 更新：Critic 更新多次（如 2 次）后 Actor 才更新一次，避免策略在未收敛的 Q 值上优化；

  • 目标策略平滑：为目标动作添加截断噪声，提升策略泛化性。

4. TD3 算法中 Critic 的更新频率一般要比 Actor 是更快还是更慢？为什么？
Critic 更新频率快于 Actor（如 Critic 更新 2 次后 Actor 更新 1 次）。因为 Critic 需优先学习准确的 Q 值估计，为 Actor 提供稳定的策略梯度；若 Actor 更新过快，可能基于未收敛的 Critic 做出错误优化，导致训练不稳定。

第十二章PPO算法

PPO算法是一种基于策略梯度的深度学习强化算法，PPO算法的主要思想是通过在策略梯度的优化过程中引入一个重要性权重来限制策略更新的幅度，从而提高算法的稳定性和收敛性。PPO算法的优点在于简单、易于实现、易于调参，应用十分广泛。

12.1 重要性采样

重要性采样是一种估计随机变量的期望或者概率分布的统计方法。

重要性采样是PPO复用历史数据的核心机制。它通过权重比将行为策略的期望值转换为目标策略的期望，显著提升样本效率。但该技术存在致命约束：当新旧策略差异过大时，权重的方差会急剧增加，导致梯度估计失真。PPO通过裁剪机制将策略更新限制在合理区间，避免因策略突变引起的训练崩溃。这一设计平衡了数据重用与稳定性，是PPO区别于传统策略梯度的关键创新。

12.2 PPO 算法

本质上PPO算法就是在Actor-Critic算法的基础上增加了重要性采样的约束而已，从而确保每次的策略梯度估计都不会过分偏离当前的策略，也就是减少了策略梯度估计的方差，从而提高算法的稳定性和收敛性。

PPO的核心是裁剪目标函数：


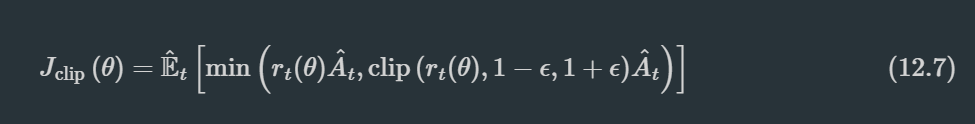
该函数通过双重约束（直接截断权重比 + 目标函数取最小值）确保策略平滑更新。其技术框架融合三大组件：

  • 广义优势估计（GAE）：平衡TD与蒙特卡洛的偏差-方差权衡；

  • 熵正则化：添加策略熵项延缓探索收敛；

  • 多步更新：提升数据利用率。
    这一设计使PPO在避免TRPO复杂二阶优化的同时，保持相近的稳定性。

12.3 一个常见的误区

PPO算法是on-policy的。

误区在于将PPO视为纯同策略（on-policy）算法。实际上，其重要性采样机制赋予了有限的异策略能力：只要行为策略与目标策略的KL散度维持在较小范围内（如D_KL< 0.05），就能安全复用旧数据。但这一条件相当严格——当策略更新过快或环境不稳定时，KL散度容易超过阈值，导致重要性权重失效。此时裁剪机制成为关键保障：通过严格控制r_t(θ)的变化幅度，避免策略崩溃。实践中需要持续监控KL值，若发现其持续上升，应及时降低学习率或增大ε值。

12.4 实战：PPO 算法

在工程实现中，需要重点关注以下三个核心环节：

  1. 网络架构设计
  • 采用Actor-Critic共享底层特征（如全连接层）的结构
  • Critic网络输出状态值V(s)
  • Actor网络输出动作分布参数：
    • 连续动作空间：高斯分布的均值和方差
    • 离散动作空间：softmax概率分布
  1. 数据预处理
  • 打乱轨迹数据以消除时间相关性
  • 采用小批量梯度下降（batch_size范围64~256）来降低方差
  1. 参数调优
  • 裁剪系数：ϵ=0.2（允许20%的策略偏移）
  • GAE参数：λ=0.95（接近蒙特卡洛的低偏差特性）
  • 熵系数：c₂=0.01（保持适度探索）
  • 学习率：3e-4（使用Adam优化器）

调试建议：

  • 监控KL散度（警戒值>0.05）
  • 观察裁剪比例（理想范围10%~30%）
  • 在Pendulum-v1环境中，PPO算法应在100回合内达到-200的奖励阈值

12.5 本章小结

PPO算法凭借其目标函数裁剪和重要性采样的协同设计，在稳定性、效率与易用性之间实现了最佳平衡，已成为工业级强化学习的首选方案。其主要优势包括：

  1. 卓越的鲁棒性：相比DDPG算法，PPO对超参数变化更不敏感，尤其适合处理图像等高维输入状态

  2. 广泛的兼容性：支持分布式训练（如Ray框架），并能通过结合RNN处理部分可观测环境

  3. 理论实践双优：避免了TRPO复杂的二阶求导，同时保持高达80%以上的GPU利用率

当前局限性主要体现在样本效率方面：相比DDPG/TD3仍有差距，在连续控制任务中收敛速度约慢30%。未来可通过PPO-kl的自适应ε调整策略，或结合模仿学习等方法来提升算法效率。

12.6习题

  1. 为什么 DQN 和 DDPG 算法不使用重要性采样技巧呢？
    DQN 和 DDPG 不使用重要性采样是因为它们基于经验回放机制处理异策略数据，且目标策略为确定性策略（如 DQN 的贪婪策略、DDPG 的确定性输出），而行为策略通过噪声探索生成动作；重要性采样在连续动作空间计算策略比率复杂且易导致数值不稳定，因此直接重用经验数据更高效。

  2. PPO 算法原理上是 on-policy 的，但它可以是 off-policy 的吗，或者说可以用经验回放来提高训练速度吗？为什么？

    PPO引入重要性采样机制，使其能够支持off-policy训练并利用经验回放。然而该方法存在严格限制：行为策略与目标策略必须保持较小差异（如KL散度较低）。当策略差异过大时，重要性权重r_t(θ)会产生显著偏差，从而影响训练效果。PPO通过设置裁剪区间[1-ε,1+ε]来约束r_t(θ)的波动范围，这一机制可在一定程度上缓解上述问题，但前提是策略更新过程必须保持足够的平滑性。

  3. PPO 算法更新过程中在将轨迹样本切分多个小批量的时候，可以将这些样本顺序打乱吗？为什么？
    必须打乱样本顺序。因为轨迹数据具有强时间相关性（如相邻状态依赖），打乱后确保每个小批量覆盖多样化的状态-动作对，打破数据关联性，从而降低梯度更新的方差，提升训练稳定性和收敛效率。

  4. 为什么说重要性采样是一种特殊的蒙特卡洛采样？

    重要性采样是一种特殊的蒙特卡罗采样方法。其核心思想是从行为策略分布中采集样本数据，然后通过乘以重要性权重r_t(θ)将其校正为目标策略的期望值。这种方法本质上是通过加权采样来实现不同分布间的无偏估计，从而显著提升了蒙特卡罗方法的数据复用能力。

第十三章SAC算法

SAC算法是一种基于最大熵强化学习的策略梯度算法，它的目标是最大化策略的熵，从而使得策略更加鲁棒。SAC算法的核心思想是，通过最大化策略的熵，使得策略更加鲁棒，经过超参改良后的SAC算法在稳定性方面是可以与PPO算法华山论剑的。

13.1 最大熵强化学习

在强化学习中，策略的选择直接决定了智能体的探索与利用能力。

  • 确定性策略（Deterministic Policy）

    • 定义：给定状态 s，策略 π 总是输出固定动作 a=π(s)。
    • 优势：
      • 稳定性与可控性：结果可复现，适合简单环境（如九宫格寻路、石头剪刀布）。
      • 高效性：无需采样，计算开销小。
    • 劣势：
      • 缺乏探索：易陷入局部最优，无法应对复杂环境中的不确定性。
      • 脆弱性：对噪声敏感，难以适应动态变化的环境。

  • 随机性策略（Stochastic Policy）

    • 定义：给定状态 s，策略 π 输出动作的概率分布 π(a∣s)。
    • 优势：
      • 灵活性：通过随机性探索未知状态，避免局部最优。
      • 鲁棒性：在噪声或对抗性环境中更具适应性（如对抗博弈、多智能体协作）。
    • 劣势：
      • 收敛速度慢：高随机性可能导致训练不稳定。
      • 复现性差：实验结果可能因随机种子不同而波动。

结论：随机性策略在复杂环境中更具优势，但需通过熵正则化等方法平衡探索与利用。

传统强化学习的目标是最大化累积奖励：

π∗=arg⁡max⁡πEπ[∑tr(st,at)]

最大熵强化学习（Maximum Entropy Reinforcement Learning, MaxEnt RL） 在此基础上引入熵约束，目标函数变为：

π∗=arg⁡max⁡πEπ[∑tr(st,at)+αH(π(⋅∣st))]

其中：

  • H(π(⋅∣s))=−Ea∼π[log⁡π(a∣s)] 是策略熵，衡量动作分布的随机性。
  • α 是温度系数（Temperature Coefficient），控制熵项权重。

核心目标：在最大化累积奖励的同时，最大化策略的熵，从而：

  1. 增强探索能力：高熵策略鼓励智能体尝试更多动作，避免过早收敛。
  2. 提高鲁棒性：随机性策略更适应环境噪声和对抗性干扰。

13.2 Soft Q-Learning

1. 核心公式

  • Soft Bellman 方程

    • Q 函数：

      Q(st,at)=r(st,at)+γEst+1[V(st+1)]

    • V 函数（Soft Value Function）：

      V(st)=αlog⁡∫exp⁡(1αQ(st,a))da

  • 值函数更新规则

    min⁡QE(s,a,r,s′)∼D[(Q(s,a)−(r+γV(s′)))2]

  • 策略提取（Soft Policy）

    π(a∣s)=exp⁡(1α(Q(s,a)−V(s)))

2. 关键特性

  • 熵正则化：在最大化累积奖励的同时最大化策略熵，鼓励探索。
  • 软贝尔曼方程：V 函数通过积分形式结合 Q 函数和熵项，体现最大熵思想。
  • 策略隐式生成：策略由 Q 和 V 函数直接推导，无需显式建模。

3. 实现挑战

  1. 积分计算困难
    • 连续动作空间下的积分无法解析求解，需通过采样近似（如重参数化技巧）。
  2. 采样效率低
    • 策略评估需多次采样动作空间，增加计算开销。
  3. 稳定性要求高
    • Q 函数和 V 函数耦合更新易导致训练不稳定，需引入双 Q 网络、目标网络等技术。

13.3 SAC

  • 最大熵目标
    SAC（Soft Actor-Critic）是一种基于最大熵框架的深度强化学习算法，目标是最大化累积奖励 和 策略的熵：

    π* = argmax E_π[∑(r(s_t,a_t) + αH(π(·|s_t)))]

    其中：

  • E_π表示策略π下的期望
  • r(s_t,a_t)是状态s_t下采取动作a_t的即时奖励
  • H(π(·|s_t))是策略在状态s_t下的熵
  • α是调节探索强度的温度参数

  • Actor-Critic框架

SAC结合了随机策略（Actor）和双Q函数估计（Critic），适用于连续动作空间任务。

SAC包含以下核心模块：

  1. Actor网络

    • 输出动作的概率分布参数（均值和标准差），用于采样动作。
    • 使用重参数化技巧（Reparameterization Trick）解决采样不可导问题。

  2. Critic网络

    • 双Q网络（Q1和Q2）：估计状态-动作对的价值，减少高估偏差。
    • 目标网络（Target Q/V）：通过软更新（Polyak平均）提高训练稳定性。

  3. 熵调节网络

    • 自动学习温度参数 αα，无需手动调参。

13.4 自动调节温度因子

在 Soft Actor-Critic (SAC) 算法中，温度因子 α 是控制累积奖励和策略熵权重平衡的关键参数。其目标函数可表示为：

π∗ = argmax Eπ[∑r(s_t,a_t) + αH(π(·|s_t))]

温度因子的影响：

  • 高 α 值：增强探索能力，策略更倾向于最大化熵
  • 低 α 值：增强利用能力，策略更关注累积奖励

实际应用中的挑战在于：

  1. 手动调节 α 需要大量实验
  2. 不同任务的最优 α 值差异显著

为此，SAC 提出了自动调节 α 的解决方案。

自动调节机制原理

SAC 采用约束优化方法动态调整 α，使其满足以下等式条件：

E_{a∼π}[-αlogπ(a|s) - αH₀] = 0

其中：

  • H₀ 表示目标熵
  • 通常设置为动作空间维度（例如 2D 动作空间对应 H₀=2）
  • 核心目标是使策略熵 H(π) 逼近 H₀，实现探索与利用的平衡

13.5 实战：SAC 算法

import torchclass Config:def __init__(self):self.algo_name = 'SAC'self.env_id = 'CartPole-v1'self.mode = 'train'self.seed = 0 # 随机种子self.max_epsiode = 100 # 训练的回合数self.max_step = 200 # 每个回合的最大步数，超过该数则游戏强制终止#region 在线测试相关参数self.online_eval_episode = 10 # 测试的回合数self.online_eval_freq = 2000 # 在线测试的频率, 模型每更新N次就测试一次#endregionself.gamma = 0.99 #折扣因子self.lambda_mean=1e-3 # 重参数化分布均值的损失权重self.lambda_std=1e-3 # 重参数化分布标准差的损失权重self.lambda_z = 0.0 # 重参数化分布抽样值的损失权重self.soft_update_tau = 1e-2 # 目标网络软更新系数self.lr_critic = 3e-4 # Q网络的学习率self.lr_actor = 3e-4 # 策略网络的学习率self.lr_alpha = 3e-4 # 温度参数的学习率self.buffer_size = 8000 # 经验回放池大小self.hidden_dim = 256 # 隐藏层维度self.batch_size  = 128 # 批次大小self.device = self._auto_get_device() # 设备def _auto_get_device(self):_device = 'cpu'if torch.cuda.is_available():_device = 'cuda'elif torch.backends.mps.is_available():_device = 'mps'return _device
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import Adam
from torch.distributions import Normal
import numpy as npclass Critic(nn.Module):def __init__(self, state_dim, action_dim, hidden_dim, init_w=3e-3):super(Critic, self).__init__()'''SoftQ'''self.layers = nn.Sequential(nn.Linear(state_dim, hidden_dim), nn.ReLU(),nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),nn.Linear(hidden_dim, action_dim))def forward(self, state):return self.layers(state)class Actor(nn.Module):def __init__(self, state_dim, action_dim, hidden_dim):super(Actor, self).__init__()self.layers = nn.Sequential(nn.Linear(state_dim, hidden_dim), nn.ReLU(),nn.Linear(hidden_dim, hidden_dim), nn.ReLU(),nn.Linear(hidden_dim, action_dim))def forward(self, state):logits = self.layers(state)probs = torch.softmax(logits, dim=-1)log_probs = torch.log_softmax(logits, dim=-1)return probs, log_probs
from collections import deque
import randomclass ReplayBuffer(object):def __init__(self, cfg: Config) -> None:self.capacity = cfg.buffer_sizeself.buffer = deque(maxlen=self.capacity)def push(self, transitions):''' 存储transition到经验回放中'''self.buffer.append(transitions)def sample(self, batch_size: int, sequential: bool = False):if batch_size > len(self.buffer): # 如果批量大小大于经验回放的容量，则取经验回放的容量batch_size = len(self.buffer)if sequential: # 顺序采样rand = random.randint(0, len(self.buffer) - batch_size)batch = [self.buffer[i] for i in range(rand, rand + batch_size)]return zip(*batch)else: # 随机采样batch = random.sample(self.buffer, batch_size)return zip(*batch)def __len__(self):''' 返回当前存储的量'''return len(self.buffer)
class Policy:def __init__(self, cfg: Config, state_dim:int, action_dim:int) -> None:self.batch_size  = cfg.batch_size self.device = torch.device(cfg.device)self.gamma = cfg.gammaself.lambda_mean = cfg.lambda_meanself.lambda_std  = cfg.lambda_stdself.lambda_z    = cfg.lambda_zself.soft_update_tau = cfg.soft_update_tau# 双Q网络self.critic_1 = Critic(state_dim, action_dim, cfg.hidden_dim).to(self.device)self.critic_2 = Critic(state_dim, action_dim, cfg.hidden_dim).to(self.device)self.critic_1_target = Critic(state_dim, action_dim, cfg.hidden_dim).to(self.device)self.critic_2_target = Critic(state_dim, action_dim, cfg.hidden_dim).to(self.device)self.critic_1_target.load_state_dict(self.critic_1.state_dict())self.critic_2_target.load_state_dict(self.critic_2.state_dict())self.actor = Actor(state_dim, action_dim, cfg.hidden_dim).to(self.device)  self.log_alpha = torch.zeros(1, requires_grad=True, device=self.device)self.opt_critic_1 = Adam(self.critic_1.parameters(), lr=cfg.lr_critic)self.opt_critic_2 = Adam(self.critic_2.parameters(), lr=cfg.lr_critic)self.opt_actor = Adam(self.actor.parameters(), lr=cfg.lr_actor)  self.opt_alpha = Adam([self.log_alpha], lr=cfg.lr_alpha) # 学习率和actor相同self.target_entropy = -np.log(1.0 / action_dim) * 0.98self.memory = ReplayBuffer(cfg)self.update_cnt = 0@torch.no_grad()def sample_action(self, state):state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)probs, _ = self.actor(state)dist = torch.distributions.Categorical(probs)action = dist.sample().item()return action@torch.no_grad()def predict_action(self, state):state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)probs, _ = self.actor(state)action = torch.argmax(probs, dim=1).item()return actiondef get_policy_params(self):'''获取策略网络的参数'''return self.actor.parameters()def set_policy_params(self, params):'''设置策略网络的参数'''for param, new_param in zip(self.actor.parameters(), params):param.data.copy_(new_param.data)def update(self):if len(self.memory) < self.batch_size: # 当经验回放中不满足一个批量时，不更新策略return states, actions, rewards, next_states, dones = self.memory.sample(self.batch_size) # 从经验回放中随机采样一个批量的转移(transition)# 将数据转换为tensorstates = torch.tensor(np.array(states), device = self.device, dtype=torch.float) # [B, state_dim]actions = torch.tensor(np.array(actions), device=self.device,  dtype = torch.int64).unsqueeze(1)  #  [B, 1]rewards = torch.tensor(rewards, device=self.device, dtype=torch.float).unsqueeze(1)   # [B, 1]next_states = torch.tensor(np.array(next_states), device=self.device, dtype=torch.float) # [batchB_size, state_dim]dones = torch.tensor(np.float32(dones), device=self.device).unsqueeze(1)  # [batch_size,1]with torch.no_grad():    probs_next, log_probs_next = self.actor(next_states) #计算t+1时刻的动作q_value_1_target = self.critic_1_target(next_states) #计算t+1时刻的q值q_value_2_target = self.critic_2_target(next_states)q_value_min = torch.min(q_value_1_target, q_value_2_target) # 计算t+1时刻的q值entropy = -torch.sum(log_probs_next * log_probs_next, dim=1, keepdim=True)q_value_target = rewards + (1 - dones) * self.gamma *  torch.sum(probs_next * (q_value_min - self.log_alpha.exp() * log_probs_next), dim=1, keepdim=True) # 计算t+1时刻的q值q_value_1 = self.critic_1(states).gather(1, actions.long()) #计算t时刻的q值q_value_2 = self.critic_2(states).gather(1, actions.long())loss_critic_1 = nn.MSELoss()(q_value_1, q_value_target) #计算q网络的损失函数loss_critic_2 = nn.MSELoss()(q_value_2, q_value_target)self.opt_critic_1.zero_grad()loss_critic_1.backward()self.opt_critic_1.step()self.opt_critic_2.zero_grad()loss_critic_2.backward()self.opt_critic_2.step()probs_new, log_probs_new = self.actor(states) #计算t时刻的动作q_value_new = torch.min(self.critic_1(states), self.critic_2(states)) #计算t时刻的q值loss_actor = (probs_new * (self.log_alpha.exp() * log_probs_new - q_value_new)).sum(dim=1).mean()self.opt_actor.zero_grad()loss_actor.backward()self.opt_actor.step()entropy = -torch.sum(probs_new * log_probs_new, dim=1, keepdim=True)loss_alpha = -(self.log_alpha * (entropy + self.target_entropy).detach()).mean()self.opt_alpha.zero_grad()loss_alpha.backward()self.opt_alpha.step()self.log_alpha.data = self.log_alpha.data.clamp(-20, 2) # 限制温度参数的范围## 软更新目标值网络参数for target_param, param in zip(self.critic_1_target.parameters(), self.critic_1.parameters()):target_param.data.copy_(target_param.data * (1.0 - self.soft_update_tau) + param.data * self.soft_update_tau)for target_param, param in zip(self.critic_2_target.parameters(), self.critic_2.parameters()):target_param.data.copy_(target_param.data * (1.0 - self.soft_update_tau) + param.data * self.soft_update_tau)self.update_cnt += 1return {'loss_critic_1': loss_critic_1.item(),'loss_critic_2': loss_critic_2.item(),'loss_actor': loss_actor.item(),'loss_alpha': loss_alpha.item()}
import gymnasium as gymclass EnvMgr:def __init__(self, cfg: Config):self.env = gym.make(cfg.env_id) # 创建环境self.eval_env = gym.make(cfg.env_id)print(f"env id: {cfg.env_id}, state_dim: {self.state_dim}, action_dim: {self.action_dim}")@propertydef action_dim(self):return self.env.action_space.n # 动作空间的维度@propertydef state_dim(self):return self.env.observation_space.shape[0]
def eval_policy(cfg: Config, policy: Policy, env):''' 测试'''rewards = []  # 记录所有回合的奖励steps = []  # 记录所有回合的步数for _ in range(cfg.online_eval_episode):ep_reward = 0  # 记录一回合内的奖励ep_step = 0state, _ = env.reset(seed = cfg.seed)  # 重置环境，返回初始状态for _ in range(cfg.max_step):action = policy.predict_action(state)  # 选择动作next_state, reward, terminated, truncated , _ = env.step(action)  # 更新环境，返回transitionstate = next_state  # 更新下一个状态ep_reward += reward  # 累加奖励ep_step += 1if terminated or truncated:breakrewards.append(ep_reward)steps.append(ep_step)return {'reward': np.mean(rewards), 'step': np.mean(steps)}def train(cfg: Config, policy: Policy, env_mgr: EnvMgr):''' 训练'''env = env_mgr.enveval_env = env_mgr.eval_envrewards = []  # 记录所有回合的奖励eval_rewards = []  # 记录所有回合的奖励best_policy_params = None  # 最佳策略best_ep_reward = float('-inf') # 最佳回合的奖励tot_step = 0policy_summary_dict = {} # 记录策略更新的参数，如损失等for i_ep in range(cfg.max_epsiode):ep_reward = 0  # 记录一回合内的奖励ep_step = 0state, _ = env.reset(seed = cfg.seed)  # 重置环境，返回初始状态for _ in range(cfg.max_step):ep_step += 1tot_step += 1action = policy.sample_action(state)  # 选择动作next_state, reward, terminated, truncated , _ = env.step(action)  # 更新环境，返回transitionpolicy.memory.push((state, action, reward, next_state, terminated or truncated))  # 保存transitionstate = next_state  # 更新下一个状态# 更新智能体，这里也可以改成每采样50步再更新50次policy_summary = policy.update()  if policy_summary is not None:for k, v in policy_summary.items():if k not in policy_summary_dict:policy_summary_dict[k] = []policy_summary_dict[k].append(v)if policy.update_cnt > 0 and policy.update_cnt % cfg.online_eval_freq == 0:eval_res = eval_policy(cfg, policy, eval_env)eval_rewards.append(eval_res['reward'])if eval_res['reward'] >= best_ep_reward:print(f"找到新的最优策略，回合：{i_ep+1}，模型步数：{policy.update_cnt}，测试奖励：{eval_res['reward']:.2f}, 测试回合长度：{eval_res['step']}")best_ep_reward = eval_res['reward']best_policy_params = policy.get_policy_params()# policy.update() ep_reward += reward  # 累加奖励if terminated or truncated:breakrewards.append(ep_reward)if (i_ep + 1) % 10 == 0:print(f"回合：{i_ep+1}/{cfg.max_epsiode}，奖励：{ep_reward:.2f}，回合长度：{ep_step}")env.close()return {'rewards':rewards, 'eval_rewards':eval_rewards, 'policy_summary_dict':policy_summary_dict,'best_policy_params':best_policy_params}
# 获取参数
cfg = Config() 
env_mgr = EnvMgr(cfg) # 创建环境
policy = Policy(cfg, env_mgr.state_dim, env_mgr.action_dim) # 创建策略
all_seed(cfg.seed)
print_cfgs(cfg)
res = train(cfg, policy, env_mgr) # 训练

码字不易，点赞收藏关注吧。

http://www.xdnf.cn/news/16710.html

相关文章：

  • C语言复习记录
  • OracleJDK和OpenJDK​区别,为什么Spring官方推荐使用OpenJDK?
  • 微服务 02
  • 2025虚幻5光明之魂开发思考1——借鉴软件工程
  • 初始sklearn 数据集获取、分类、划分与特征工程
  • 元素定位常见问题
  • Redis线程模型讨论
  • Flutter兼容的iOS的最低版本号
  • Java 大视界 -- Java 大数据在智能医疗远程健康监测与疾病预防预警中的应用（374）
  • 【IQA技术专题】DISTS代码讲解
  • Git 详细安装配置教程（Windows版）
  • 【每日一错】mysql账户及权限删除
  • 计数组合学7.9（ 标量积)
  • vk框架或者普通函数封装的一些函数可以拿取使用【会持续更新】
  • [特殊字符] 数据可视化结合 three.js：让 3D 呈现更精准，3 个优化经验谈
  • 2025年物联网新趋势：格行随身WiFi的模块化架构与低延迟优化
  • 【09】大恒相机SDK C#开发 ——库函数 IntPtr ConvertToRGB24详细解释 及 示例
  • 【烧脑算法】Dijkstra 算法：解决最短路问题
  • Unity_数据持久化_PlayerPrefs存储各数据类型
  • 【爬虫实战】使用Python和JS逆向基于webpack的游戏平台
  • 【Java安全】CC1链
  • 计算机网络：什么是光猫
  • 安卓脱壳指南
  • 5G毫米波射频前端设计：从GaN功放到混合信号集成方案
  • TDengine 中 TDgp 中添加算法模型（预测分析）
  • 通过 Docker Compose 快速部署RocketMQ 服务
  • openKylin 2.0 SP2揭秘 - 磐石架构：不变的核心，更好的体验
  • 从 MySQL 迁移到 TiDB：使用 SQL-Replay 工具进行真实线上流量回放测试 SOP
  • Video_1920×1080i 1920_1080p
  • 基于 BiLSTM+自注意力机制(改进双塔神经网络) 的短文本语义匹配