当前位置：首页 > ops >正文

Python之--集合

ops 2025/7/26 12:34:19

定义

（1）Python 中的集合与数学中集合的概念一致

（2）Python 中的集合是一个无序的不重复元素序列

（3）集合中只能存储不可变数据类型（创建后其值不能被修改，比如数字（int、float等）、字符串（str）、元组（tuple））

（4）在 Python 中集合使用 { } 定义

（5）与列表、字典一样，都是 Python 中的可变数据类型（在不改变其标识（内存地址）的情况下，可以修改其值的数据类型，其支持添加、删除元素等操作，在进行这些操作时，集合对象本身的内存地址没有改变，但是集合中的元素却发生了变化。）

集合的优势

1、去重（如 set([1,1,2]) 直接得到 {1,2} ）

lst = [1, 2, 2, 3, 3, 3, "apple", "apple"]
unique_lst = list(set(lst))
print(unique_lst)
# 输出: [1, 2, 3, 'apple']

在上面这段代码中，首先将列表 lst 转换为集合，由于集合中元素不能重复，重复的数字和字符串会被自动去除，然后再将集合转换回列表，就得到了去重后的列表。

2、快速判断元素是否存在（基于哈希表，查询效率高）

my_set = {1, 2, 3, 4, 5}
print(3 in my_set)  # 输出: True
print(6 in my_set)  # 输出: Falsemy_list = [1, 2, 3, 4, 5]
print(3 in my_list)  # 输出: True
print(6 in my_list)  # 输出: False

3、数学集合运算

a = {1, 2, 3}
b = {2, 3, 4}# 1. 交集（&）：同时属于 a 和 b 的元素
print("交集:", a & b)  # 输出 {2, 3}# 2. 并集（|）：属于 a 或属于 b 的所有元素（去重）
print("并集:", a | b)  # 输出 {1, 2, 3, 4}# 3. 差集（-）：属于 a 但不属于 b 的元素
print("差集:", a - b)  # 输出 {1}# 4. 对称差集（^）：属于 a 或 b，但不同时属于两者的元素（类似“补集”常用场景）
print("对称差集（补集常用实现）:", a ^ b)  # 输出 {1, 4}

集合的创建方式

1、使用 { } 直接创建集合

语法结构如下:

s={element1,element2,......elementN}

s = {1, 2, 3, "apple"}

**特点：直接枚举元素，元素需是不可变类型（如数字、字符串、元组），且自动去重（重复元素会被合并）。

**注意：空 { } 会被识别为字典，若要创建空集合，必须用 set() 。

2、使用内置函数 set() 创建集合

语法结构如下:

s=set(可迭代对象)

# 从列表创建集合（自动去重）
s1 = set([1, 2, 2, 3])  # 从字符串创建集合（按字符拆分去重）
s2 = set("hello")  #创建空集合
empty_set = set()
print(empty_set)
print(type(empty_set))

特点：接收可迭代对象（如列表、字符串、元组等），自动遍历并生成集合，同样会去重。

分辨是字典还是集合的方法

主要是从定义语法区分：

字典（dict）的语法特征：用 { } 定义，元素是键值对（key: value）的形式

# 字典：每个元素是 key:value
my_dict = {'name': '小明', 'age': 18}

空字典：单独的 {} 就是空字典（若要空集合得用 set() ）：

empty_dict = {}  # 这是空字典

集合（set）的语法特征：用 { } 定义时，元素是单个值（不能有 key: value ）；或用 set() 函数创建。

# 集合：元素是单个值，自动去重
my_set = {1, 2, 3, 3}  # 实际存储 {1, 2, 3}
# 用 set() 函数创建（常用语空集合或转换可迭代对象）
empty_set = set()  
set_from_list = set([1, 2, 2])  # 结果 {1, 2}

**关键区别就是集合里只有 “独立元素”，字典里是 “键值对” 。

集合的删除

s = {1, 2, 3}
del s  # 删除集合 s，释放内存
# print(s)  # 报错：NameError（s 已被删除）

作用：彻底删除集合对象本身，而非仅删除元素。若后续代码再使用该集合名，会提示未定义。

集合的操作符

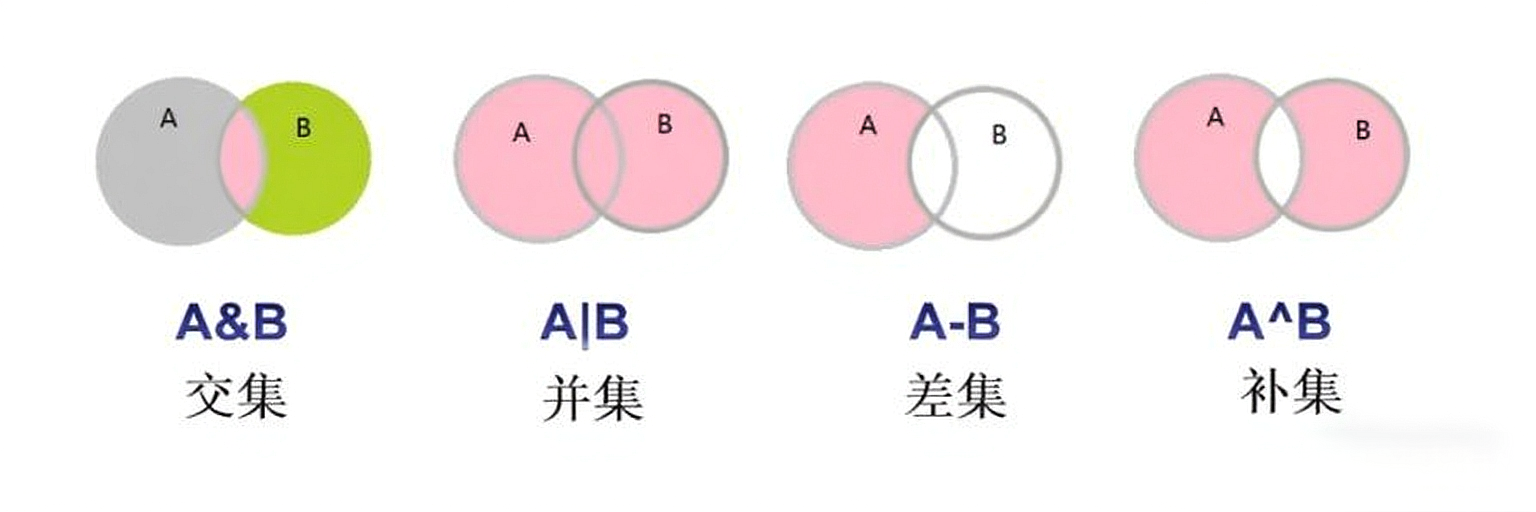
a = {1, 2, 3}
b = {2, 3, 4}# 1. 交集（&）：同时属于 a 和 b 的元素
print("交集:", a & b)  # 输出 {2, 3}# 2. 并集（|）：属于 a 或属于 b 的所有元素（去重）
print("并集:", a | b)  # 输出 {1, 2, 3, 4}# 3. 差集（-）：属于 a 但不属于 b 的元素
print("差集:", a - b)  # 输出 {1}# 4. 对称差集（^）：属于 a 或 b，但不同时属于两者的元素（类似“补集”常用场景）
print("对称差集（补集常用实现）:", a ^ b)  # 输出 {1, 4}

集合的相关操作

集合的方法	描述说明
s.add(x)	如果 x 不在集合 s 中，则将 x 添加到集合 s
s.remove(x)	如果 x 在集合中，将其删除，如果不在集合中，程序报错
s.clear()	清除集合中所有元素

# 创建一个集合
s = {1, 2, 3}# s.add(x)：添加元素 4，因为 4 不在集合中，添加后集合变为 {1, 2, 3, 4}
s.add(4)
print(s)# s.remove(x)：删除元素 3，3 在集合中，删除后集合变为 {1, 2, 4}
s.remove(3)
print(s)try:# 尝试删除不存在的元素 5，会报错 KeyErrors.remove(5)
except KeyError as e:print(f"报错：{e}")# s.clear()：清除集合中所有元素，集合变为空集合 set()
s.clear()
print(s)

集合的遍历

# 集合的遍历操作
for item in s:print(item)# 使用enumerate()函数
for index,item in enumerate(s):print(index,'--->',item)

集合的生成式

基本语法

{表达式 for 变量 in 可迭代对象 [if 条件]}

# 从列表生成集合，自动去重
lst = [1, 2, 2, 3, 3, 3]
s = {x for x in lst}
print(s)  # 输出: {1, 2, 3}

总结

对这几天学习的这几种数据类型进行总结：

数据类型	序列类型	元素是否可重复	是否有序	定义符号
列表 list	可变序列	可重复	有序	[ ]
元组 tuple	不可变序列	可重复	有序	( )
字典 dict	可变序列	Key 不可重复 Value 可重复	无序	{key:value}
集合 set	可变序列	不可重复	无序	{ }