当前位置：首页 > ops >正文

模拟IC设计基础系列6-差动放大器 Differential AMP

ops 2025/6/20 17:48:11

1. 模拟电路设计绪论

6. 差动放大器 Differential AMP

6.1 差分输入

在电路的实际工作中，往往存在各种干扰(例如VDD和GND的波动、金属线的电容耦合等)，而模拟电路对干扰非常敏感，所以我们需要一种电路结构来抑制这种影响。

6.1.1 差分信号

在这里插入图片描述
图1.一个信号可以被拆解成差分信号表示
定义共模电平(Common mode Level)
$V_{CM} : {V_{CM}} = \frac{{{V_{in1}} + {V_{in2}}}}{2} = {V_B}$
共模电平确定了电路的工作点电压，我们希望它没有扰动，是个固定值
定义差模电平(Differential mode Level)
$V_{diff} : {V_{diff}} = {V_{in1}} - {V_{in2}} = {v_{in}}$
而对于任意的两个输入vin1，vin2，可以将它们拆解为两部分：
$\left\{ \begin{array}{l} {v_{CM}} = \frac{{{v_{in1}} + {v_{in2}}}}{2} (共模部分) \\ {v_{diff1}} = \frac{{{v_{in1}} - {v_{in2}}}}{2}(差模部分)\\ {v_{diff2}} = \frac{{{v_{in2}} - {v_{in1}}}}{2}(差模部分) \\ \end{array} \right.$

6.1.2 差分放大的优点

6.1.2.1 消除电压波动带来的影响

在这里插入图片描述
当电源VDD上有一个电压噪声vn，使用差分结构可以消除噪声干扰
在小信号模型中，若电源VDD上有一个电压噪声vn，那么我们可以从分压的角度来观察vn对vout的影响：从MOS的漏极看下去，得到的是一个很大的小信号电阻ro，通常远大于RD，于是从分压的角度来看，电压噪声几乎全部全部降落在ro1上，即vn的波动几乎完全加在vout上。
我们令两边输入大小相同，相位相反；且左右两边完全对称：
$\left\{ \begin{array}{l} {v_{in1}} = {v_{in}}\\ {v_{in2}} = - {v_{in}}\\ {g_{m1}} = {g_{m2}} = {g_m}\\ {v_{out1}} = - {g_{m1}}{R_D}{v_{in1}} + {v_n}\\ {v_{out2}} = - {g_{m2}}{R_D}{v_{in2}} + {v_n} \end{array} \right.$
解得： ${v_{out1}} - {v_{out2}} = - 2{g_m}{R_D}{v_{in}}$
从结果看出，使用差分结构可以有效地消除一些电路中的噪声

6.1.2.2 大输出摆幅

单端的共源放大器的输出范围以及输出摆幅为：
$\left\{ \begin{array}{l} {V_{output}} \ge {V_{GS}} - {V_{TH}} = {V_{od}}(保证共源管饱和)\\ {V_{output}} \le {V_{DD}}(共源管截止，无电流)\\ {V_{Swing}} = {V_{DD}} - {V_{od}} \end{array} \right.$
而对于差分结构，当左边vin1增大时，vout1降低；同时右边vin2减小，vout2增大。
两边反相变化，若vout1达到最小时，vout2达到最大，vout1-vout2有最小值，反之亦然，那么有： $\left\{ \begin{array}{l} {V_{output}} \ge {V_{od}} - {V_{DD}}\\ {V_{output}} \le {V_{DD}} - {V_{od}}\\ {V_{Swing}} = 2({V_{DD}} - {V_{od}}) \end{array} \right.$
由上式可知，差分结构的输出电压摆幅为单端的两倍

6.1.3 差分放大的缺点

第一、对称的结构需要双倍的面积，双倍的直流功率。
第二、噪声电压同时加在两边的电路，使得噪声造成的功率消耗变为原来的两倍，而功率是无法用差分结构抵消的。

6.2 基本差动对

6.2.1 基本差动对的结构

在这里插入图片描述
左边的结构有一个问题，当共模电压VCM波动，M1、M2的直流工作点就会同时上下波动，跨导和电流有较大变化，使得差分工作不稳定，这种结构也被称为伪差分（pseudo differential）。
为了改进这一个问题，可以在差放的下面接一个尾电流源，当电路左右对称时，两边电流平均分配尾电流源的电流，有如下关系： ${I_{D1}} = {I_{D2}} = {I_{SS}}/2$
而输出电压的共模电平为： ${V_{out,CM}} = {V_{DD}} - {R_D}{I_{SS}}/2$

当M1、M2同时工作在饱和区时，即使输入vin的共模电压发生了变化，但电流源决定了电流大小，电流源为了保证电流不变，会将P点电压Vp提高，保证VGS1、VGS2不变，使得两边流过的电流仍然不变，输出电平也不变，以此消除共模电压波动对直流工作点的影响。

带尾电流源的差分放大结构的基本原理就是利用两边电路对Iss的分配。由于总的电流不变，若vin1提高，vin2降低，左边的电路会分配到更多的电流，而右边的电路只能分到更少的电流。
在这里插入图片描述
在实际电路中，我们往往会使用MOS电流源来作为尾电流源

6.2.2 工作状态的定性分析

以MOS电流源为尾电流源的差放结构为例进行分析

6.2.2.1 差模输入电压对差动对的影响

在这里插入图片描述

Vin摆幅过大，导致一边MOS管截止，一边导通，电流全部从一边流过
随着vin的变化，M1、M2的VGS不断变化，两个MOS管不停地“争抢”电流，而电流流过电阻，使得电流的变化最终引起输出电压的变化（Vout=Vdd-IR）
此时，输出电压和输入电压的关系为：
在这里插入图片描述

可以看到，在Vin1-Vin2=0时，Vout1-Vout2的曲线斜率有最大值，若定义差模增益为：
${A_{DM}} = \frac{{{v_{out,diff}}}}{{{v_{in,diff}}}} = \frac{{{v_{out1}} - {v_{out2}}}}{{{v_{in1}} - {v_{in2}}}}$
即当Vin1-Vin2=0时，差分放大的差模增益取最大值
同时，对某一边的电路来说，输出电压Vout的摆幅为：
$\left\{ \begin{array}{l} {V_{out,\min }} = \max ({V_{DD}} - {R_D}{I_{SS}},{V_{in,CM}} - {V_{TH}})\\ {V_{out,\max }} = {V_{DD}} \end{array} \right.$
（加上差分信号后）随着Vin的提高，电路分到的电流I提高，若R过大则可能导致Vout降低较多，这可能导致M1进入线性区，那么 ${V_{out,\min }} = {V_{in,CM}} - {V_{TH}}$ ；若M1不进入线性区，当一边的电路流过所有的电流Iss时，Vout有最小值， ${V_{out\min }} = V_{DD}-R_{D}I_{SS}$ 。

而当Vin降低，直到管子截止，则该支路没有电流流过，R没有分压（被截止的MOS分走了），Vout有最大值 ${V_{out,\max }} = {V_{DD}}$

6.2.2.2 共模输入电压对差动对的影响

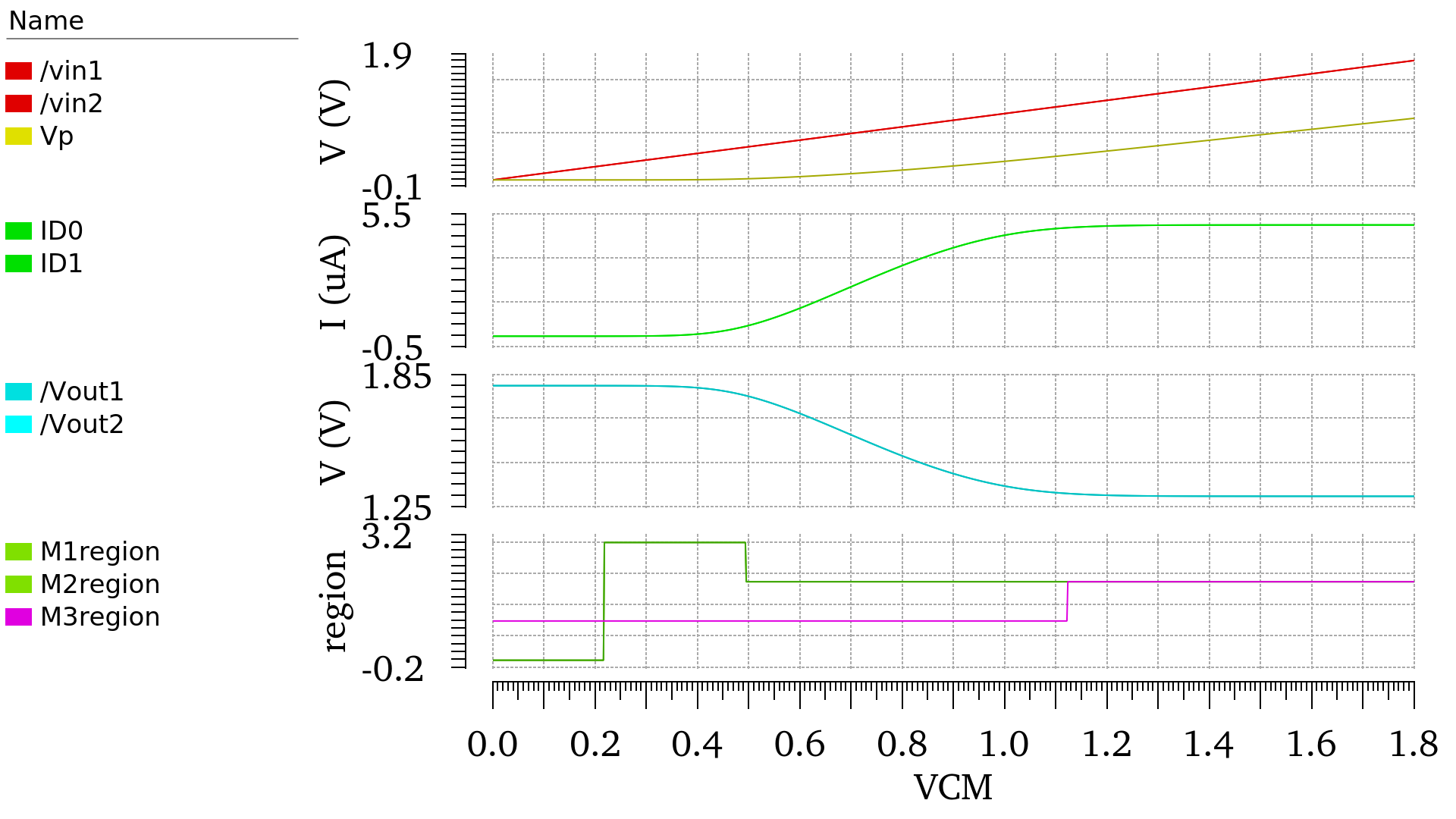
在这里插入图片描述
这里仿真用的电流源其实是Cascode电流镜，M3实际上是Cascode电流镜的共源管
1、一开始随着VCM的提高，M1、M2管从截止区进入亚阈值区，此时的电流依然很小，Vp稍微上升，电流镜M3维持在线性区即可提供很小的电流。

2、当VCM大于阈值电压Vth，M1、M2进入饱和区，但它俩产生的电流之和依旧较小，无法让电流镜管饱和。

3、随着VCM增加，电流增加，为了提高流过M3的电流，Vp自适应地提高。直到VCM足够大之后，两个管子产生的电流才足以让M3管饱和。

4、在M3管饱和以后，当VCM继续增大，电流却被尾电流源限制不能继续增大，因此Vp自适应地提高，让M1、M2的VGS减小（同时衬偏效应影响加重，M1、M2的VTH提高，这也抑制了电流的增大），抑制电流的增大。

根据上面的分析，共模输入电压的摆幅为：（左右两边电路对称，取一边分析）

$\left\{ \begin{array}{l} {V_{in,CM\min }} = {V_{TH1}} + {V_{od1}} + {V_{od3}}\\ {V_{in,CM\max }} = \min ({V_{DD}},{V_{DD}} - {R_D}{I_{SS}}/2 + {V_{TH1}}) \end{array} \right.$
共模输入电压的最小值是为了保证M1、M3管工作在设计好的饱和区中

共模输入电压的最大值分两种情况，一种是随着VCM的增大，由于尾电流源的沟道长度调制效应，Iss增大，若尾电流源的输出阻抗过小或电阻RD过大，Vout会下降较大，可能会使得M1管进入线性区，此时的 ${V_{in,CM\max }} = {V_{DD}} - {R_D}{I_{SS}}/2 + {V_{TH1}}$ ；反之，若直到VCM=VDD之后M1也没有进入非线性区，那么 ${V_{in,CM\max }} = {V_{DD}}$ 。

6.2.3 差模增益 A_{DM}

在定性了解差分放大器的工作状态后，我们对差放的差模增益进行定性分析
${A_{DM}} = \frac{{{v_{out,diff}}}}{{{v_{in,diff}}}} = \frac{{{v_{out1}} - {v_{out2}}}}{{{v_{in1}} - {v_{in2}}}}$

6.2.3.1 大信号分析

首先，差分输出电压可以表示为：
${V_{out1}} - {V_{out2}} = ({V_{DD}} - {I_{d1}}{R_{D1}}) - ({V_{DD}} - {I_{d2}}{R_{D2}}) = - ({I_{D1}} - {I_{D2}}){R_D}$
下面我们求电流和输入电压的关系：
${V_{in1}} - {V_{GS1}} = {V_{in2}} - {V_{GS2}}$
即 ${V_{in1}} - {V_{in2}} = {V_{GS1}} - {V_{GS2}}$
而VGS可以表示为： ${V_{GS}} = {V_{od}} + {V_{TH}} = \sqrt {\frac{{2{I_D}}}{{{\mu _n}{C_{ox}}W/L}}} + {V_{TH}}$
那么有 ${V_{in1}} - {V_{in2}} = {V_{GS1}} - {V_{GS2}} = \sqrt {\frac{{2{I_{D1}}}}{{{\mu _n}{C_{ox}}W/L}}} - \sqrt {\frac{{2{I_{D2}}}}{{{\mu _n}{C_{ox}}W/L}}}$
将上式平方处理得： ${\left( {{V_{in1}} - {V_{in2}}} \right)^2} = \frac{2}{{{\mu _n}{C_{ox}}W/L}}({I_{SS}} - 2\sqrt {{I_{D1}}{I_{D2}}} )$
又 $4{I_{D1}}{I_{D2}} = {({I_{D1}} + {I_{D2}})^2} - {({I_{D1}} - {I_{D2}})^2} = {I_{SS}}^2 - {({I_{D1}} - {I_{D2}})^2}$
代入，最后计算得：
${I_{D1}} - {I_{D2}} = \frac{1}{2}{\mu _n}{C_{ox}}\frac{W}{L}\left( {{V_{in1}} - {V_{in2}}} \right)\sqrt {\frac{{4{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}} - {{\left( {{V_{in1}} - {V_{in2}}} \right)}^2}}$
定义
$\left\{ \begin{array}{l} {I_{D1}} - {I_{D2}} = {I_{d,diff}}\\ {V_{in1}} - {V_{in2}} = {V_{in,diff}} \end{array} \right.$
同单端分析相似，我们得到差放的等效跨导Gm：
${G_m} = \frac{{\partial {I_{D,diff}}}}{{\partial {V_{in,diff}}}} = \frac{1}{2}{\mu _n}{C_{ox}}\frac{W}{L}\frac{{\frac{{4{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}} - 2V_{in,diff}^2}}{{\sqrt {\frac{{4{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}} - V_{in,diff}^2} }}$
并且我们令 $\left| {{v_{in,diff}}} \right| \ge \sqrt {\frac{{2{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}}}$ 时，Gm=0，因为大于这个值时，Gm的负值没有物理意义。
在这里插入图片描述
差分输入电压与差分电流的关系

差分输入电压与等效跨导Gm的关系（对上图求导）
同时，M1、M2管的过驱动电压Vod又可以表示为：
${V_{od}} = \sqrt {\frac{{2{I_D}}}{{{\mu _n}{C_{ox}}W/L}}} = \sqrt {\frac{{{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}}}$
即差分输入电压的范围可以表示为：
$\left| {{v_{in,diff}}} \right| \leq \sqrt {\frac{{2{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}}} = \sqrt{2}{V_{od}}$
上式说明差分输入的范围取决于M1、M2管的过驱动电压，为了获得大的输入摆幅，就需要大的过驱动电压。

从物理意义上，这个可以理解为：当差分信号相差 \sqrt{2}V_{od} 时，电流已经几乎分配到一边，另一边没有电流，再继续增大差分电压几乎对电流分配没有影响。

而当 V_{in,diff}=0 时，Gm化简为： {G_m} = \sqrt {{I_{SS}}{\mu n}{C{ox}}\frac{W}{L}} = \sqrt {2\frac{{{I_{SS}}}}{2}{\mu n}{C{ox}}\frac{W}{L}} = {g_{m1}} = {g_{m2}} \由上式可知，当在共模电位上加一个差模小信号 \Delta v_{in,diff} 时，此时等效跨导达到最大且为Gm=gm1=gm2，产生的差分电流为 i_{d,diff} = G_m \Delta v_{in,diff} ，差分电流导致差分输出电压为 -G_m \Delta v_{in,diff}R_D 。过程描述如下：

1、一边增加了 \Delta v_{in,diff}/2 ，而另一边减少了 \Delta v_{in,diff}/2 ；

2、则一边的电流增加了 G_m \Delta v_{in,diff}/2 ，另一边减小了 G_m \Delta v_{in,diff}/2 ；

3、导致一边的电阻多分压 G_m \Delta v_{in,diff}R_D/2 ，另一边少分压 G_m \Delta v_{in,diff}R_D/2 ;

4、最后一边的Vout降低 G_m \Delta v_{in,diff}R_D/2 ，另一边增加 G_m \Delta v_{in,diff}R_D/2 ；

根据上面分析，当 V_{in,diff}=0 时，差模增益有最大值为： {A_{v,diff}} = - {G_m}{R_D} = - \sqrt {{I_{SS}}{\mu n}{C{ox}}\frac{W}{L}} {R_D} \

从前面的计算我们知道Gm可以表示为： {G_m} = \frac{{\partial {I_{D,diff}}}}{{\partial {V_{in,diff}}}} = \frac{1}{2}{\mu n}{C{ox}}\frac{W}{L}\frac{{\frac{{4{I_{SS}}}}{{{\mu n}{C{ox}}W/L}} - 2V_{in,diff}^2}}{{\sqrt {\frac{{4{I_{SS}}}}{{{\mu n}{C{ox}}W/L}} - V_{in,diff}^2} }} \

下面我们看一下改变Iss和W/L对Gm的影响：

1、Iss的影响：更大的Iss使得当电流仅流过一边电路时有更大的值，同时更大的Iss能带来更大的跨导。
在这里插入图片描述

2、W/L的影响：更大的W/L使得对于相同的vin,diff而言，电流变化更大，使得电流更快地被分配，因此增加了有效跨导Gm，但同时也减低了Vin,diff的输入摆幅（因为电流更快地被分配到某一边了）。

2.3.2 小信号分析——半边电路法

上面的大信号分析详细地计算了等效跨导及差模增益，下面我们用小信号进行半边电路法分析：

在这里插入图片描述
首先，我们分析P点的情况：在小信号时，若左边输入为+vin，右边输入-vin，若认为gm1=gm2，那么两边的增减的电流正好抵消，总电流没有变化，M3的状态不变，Vp没有波动。因此我们可以近似地认为P点为交流地。

那么，在分析小信号时，原本的电路可以等效为右图的结构，M1、M2可以被视为两个CS AMP的结构： \left{ \begin{array}{l} \frac{{{v_{out1}}}}{{{v_{in1}}}} = - {g_{m1}}{R_D}\ \frac{{{v_{out2}}}}{{{v_{in2}}}} = {g_{m2}}{R_D} \end{array} \right. \ 那么差模增益为： {A_{v,DM}} = \frac{{{v_{out1}} - {v_{out2}}}}{{{v_{in}} - ( - {v_{in}})}} = \frac{{{v_{out1}}}}{{2{v_{in}}}} - \frac{{{v_{out2}}}}{{2{v_{in}}}} = - \frac{1}{2}({g_{m1}} + {g_{m2}}){R_D} = - {g_m}{R_D} \ 2.3.3 P点的详细分析

上面的小信号分析中，我们认为相反的小差分信号增减的电流相同，所有不改变总电流，使得Vp不变。而实际上，若差分输入不是小信号，那我们必须考虑到gm的特性：
在这里插入图片描述
当差分输入是小信号时，我们可以忽视Vin对直流工作点的影响，认为±vin导致的电流增减相同；但当差分输入是大信号时，就需要考虑Vin对直流工作点的影响：可以看到，当一边输入+vin时，这一边的gm增大；另一边输入-vin，gm减小，所以实际上+vin产生的电流是大于-vin减小的电流的。因此，Vp上升，一方面是降低+vin管子的Vod（降低VGS和提高VTH），另一方面是提高电流源管的沟道长度调制效应，使得流过M3的电流也会略有提高。
在这里插入图片描述
从上图可以看到，和之前分析的一样，由于提高的电流总是大于降低的电流，使得电压源上方的Vp总是会随着多出来的电流一起变化。

同时，我们可以发现，Vp的频率其实是为vin的两倍，因此，这种结构还可以用来做简单的倍频器。

6.2.4 带源极负反馈的差动对

在这里插入图片描述
带源极负反馈的差动对及其半边电路
从这种结构的小信号的半边电路可以发现，这种结构使得半边电路从原来的CS AMP变为带源极负反馈的CS AMP，这种结构在单端放大器中已经分析过，其优点为提高跨导的线性度，代价是降低了跨导的值：
${g_{m1}} = {g_{m2}} = {g_{m,eff}} = \frac{1}{{\frac{1}{{{g_m}}} + {R_s}}}$
此时，输入信号的范围也被提高：
$\left| {{v_{in,diff}}} \right| \ge \sqrt {\frac{{2{I_{SS}}}}{{{\mu _n}{C_{ox}}W/L}}} + {I_{SS}}{R_S} = \sqrt 2 {V_{od}} + {I_{SS}}{R_S}$
但是这种结构在直流情况下，Rs上会有一定的压降，将M1、M2的源极电压抬高，使其更容易进入线性区，导致Vout的摆幅降低。
为了解决直流压降的问题，一种实用的结构被提出：
在这里插入图片描述
带源极负反馈的差放的实用电路
对于上图中的结构，在直流情况下，电流不流过2Rs，只有当两边电流有变动时，电流才会流过中间电阻。而这种结构的小信号交流地位于2Rs中间，因此其小信号等效电路为右图，同之前的结构一样。但是这种结构避免了Rs的直流压降，不会导致输出摆幅降低。
在这里插入图片描述

上面的仿真中，后缀带R的代表是带源极负反馈的结果，没有R后缀的是普通的差放输出结果作为参照。
可以看到，由于Rs提高了Gm的线性度，那么也提高了Vout的线性度。
当正常工作在理想情况下，VCM的变化不会引起电流的变化，因此输出电压也不会变化。

6.3.1 非理想因素

1、有限的电流源输出阻抗

由于MOS电流源的沟道长度调制效应，尾电流源的输出阻抗不是无穷大（普通电流镜是ro，Cascode电流镜是 g_mr_o^2 ）。这就导致随着共模电压VCM提高，为了保证电流不变，Vp提高（降低VGS，衬偏效应->提高Vth），但在Vp提高的同时，电流源流过的电流会逐渐增大，但此时两边RD相等，所以输出电压没有差分输出：
${V_{CM}} \uparrow \Rightarrow {I_D} \uparrow \Rightarrow {I_D}{R_D} \uparrow \Rightarrow {V_{out}} \downarrow \Rightarrow \Delta {V_{out}} = 0$
2、差动对失配（不对称）
不对称的可能包括W/L，阈值电压VTH，电阻RD

6.3.2 多个非理想因素的共同效果——失调

若以上两种非理想因素同时存在，则会导致电路的失调。
当VCM波动，左右两边产生的电流波动不同，Iss的增量被不平均地分配，不同的电流流过不同的电阻又会引起两边输出电压Vout不同的波动： $\Delta {V_{CM}} \Rightarrow \Delta {I_{D1}} \ne \Delta {I_{D2}} \Rightarrow \Delta {I_{D1}}{R_{D1}} \ne \Delta {I_{D2}}{R_{D2}} \Rightarrow \Delta {V_{out}} \ne 0$
这样导致共模电压的变化引起差模的输出变化，这不是我们想要的。

6.3.3 失调的计算

6.3.3.1 有限的电流源电阻

在这里插入图片描述
从P点看下去，M3可以视为一个大电阻ro
当仅考虑共模输入时，可以将电路结构等效为右图的结构，其中 ${g_{m,eff}} = {g_{m1}} + {g_{m2}} = 2{g_m}$ ， ${R_D}\parallel {R_D} = {R_D}/2$ 。
直接用单端AMP的结论，那么对于共模输入，电路的共模输出增益为：
${A_{v,CM}} = \frac{{{v_{out,CM}}}}{{{v_{in,CM}}}} = \frac{1}{{\frac{1}{{2{g_m}}} + {r_o}}}{R_D}/2$
当ro趋近于+∞时，共模增益趋近于0。

6.3.3.2 RD失配

在这里插入图片描述
当仅考虑RD的失配时 ${R_{D2}} = {R_{D1}} + \Delta {R_D}$ ，若共模电压产生一个波动 $\Delta V_{in,CM}$ ，则会引起电流变化 $\Delta {I_{total}} = {G_m}\Delta {V_{in,CM}} = \frac{1}{{\frac{1}{{{g_{m,eff}}}} + {r_o}}}\Delta {V_{in,CM}} = \frac{{{g_{m1}} + {g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}$
其中，M1、M2的电流可以单独表示为： $\left\{ \begin{array}{l} \Delta {I_{D1}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m1}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}\\ \Delta {I_{D2}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}} \end{array} \right.$
则输出电压的变化为：
$\left\{ \begin{array}{l} \Delta {V_{out1}} = \Delta {I_{D1}}{R_D} = \frac{{{g_{m1}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}{R_D}\\ \Delta {V_{out2}} = \Delta {I_{D2}}({R_D} + \Delta {R_D}) = \frac{{{g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}({R_D} + \Delta {R_D}) \end{array} \right.$
那么差分输出电压为（近似地认为gm1=gm2=gm）：
${V_{out,diff}} = \Delta {V_{out1}} - \Delta {V_{out2}} \approx \frac{{{g_m}}}{{1 + 2{g_m}{r_o}}}\Delta {R_D}*\Delta {V_{in,CM}}$

6.3.3.3 M1、M2失配

在工艺制造中，MOS管的宽长比W/L以及阈值电压VTH可能会有误差从而导致跨导gm的误差，最终使得电路失配。
由上面分析可知，当Vin,CM波动时，两边的电流波动可以表示为：
$\left\{ \begin{array}{l} \Delta {I_{D1}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m1}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}\\ \Delta {I_{D2}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}} \end{array} \right.$
那么，两边流过电流之差为：
$\Delta {I_{D1}} - \Delta {I_{D2}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m1}} - {g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}$
电流差导致的输出电压只差为：
$\Delta {V_{out1}} - \Delta {V_{out2}} = - \Delta {I_{D1}}{R_D} - ( - \Delta {I_{D2}}{R_D}) = - \left( {\Delta {I_{D1}} - \Delta {I_{D2}}} \right){R_D}$
定义共模到差模的增益 $A_{CM\_DM}$ 为：
${A_{CM\_DM}} = \frac{{\Delta {V_{out1}} - \Delta {V_{out2}}}}{{\Delta {V_{in,CM}}}} = \frac{{{v_{out,diff}}}}{{{v_{in,CM}}}} = - \frac{{{g_{m1}} - {g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}{R_D}$
而这种增益是我们不想要的，需要我们想办法减小。

6.3.3.4 同时考虑RD和MOS的失配

两边同时流过的电流之差仍然为： $\Delta {I_{D1}} - \Delta {I_{D2}} = {G_m}\Delta {V_{in,CM}} = \frac{{{g_{m1}} - {g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {V_{in,CM}}$
但由于两边电阻的失配，导致两边的输出电压之差有所变化： $\Delta {V_{out1}} - \Delta {V_{out2}} = - \Delta {I_{D1}}{R_D} - [ - \Delta {I_{D2}}({R_D} + \Delta {R_D})] = - \left( {\Delta {I_{D1}} - \Delta {I_{D2}}} \right){R_D} + \Delta {I_{D2}}\Delta {R_D}$
那么最终的共模到差模的增益为： ${A_{CM\_DM}} = - \frac{{{g_{m1}} - {g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}{R_D} + \frac{{{g_{m2}}}}{{1 + ({g_{m1}} + {g_{m2}}){r_o}}}\Delta {R_D}$

6.3.4 CMRR (Common Mode Rejection Ratio)共模抑制比

首先，我们令gm为平均跨导，以及gm1、gm2的偏差为：
$\left\{ \begin{array}{l} {g_m} = ({g_{m1}} + {g_{m2}})/2\\ \Delta {g_m} = {g_{m1}} - {g_{m2}} \end{array} \right.$
那么共模抑制比CMRR为： $\left| {\frac{{{A_{DM}}}}{{{A_{CM\_DM}}}}} \right| = \frac{{{g_m}{R_D}}}{{\left| {\frac{{\Delta {g_m}{R_D}}}{{1 + 2{g_m}{r_o}}}} \right|}} = \frac{{{g_m}}}{{\left| {\Delta {g_m}} \right|}}(1 + 2{g_m}{r_o})$
共模抑制比是差模增益/共模到差模的增益，差模增益是我们所需要的，而共模到差模的增益是我们不想要的，因此这个比值越大越好。（工程上也可以是反过来的比例）