当前位置：首页 > news >正文

时域抽样定理，信号重建，附带频域抽样定理

news 2025/6/7 3:24:37

1.时域抽样定理推导

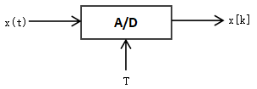
对连续时间信号 $x(t)$ 以时间间隔T进行时域抽样，得到离散抽样信号 $x[k]$ ,

即： $x[k]=x(kT)=x(t)|_{t=kT},k\in Z$

其中T为抽样间隔，抽样频率 $f_{s}=\tfrac{1}{T}$ ，抽样角频率 $\omega _{s}=\tfrac{2\pi }{T}$

设 $X(j\omega )$ 与 $X(e^{j\Omega })$ 分别表示连续时间信号 $x(t)$ 和离散时间信号 $x[k]$ 的频谱，

即： $X(j\omega )=\int_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$

$X(e^{j\Omega })=\sum_{k=-\infty }^{+\infty }x[k]e^{-j\Omega k}$

抽样信号可表示为： $x_{s}(t)=x(t)\delta _{T}(t)$

对 $x_{s}(t)$ 进行连续时间Fourier变换，并利用Fourier的乘积特性，可得：

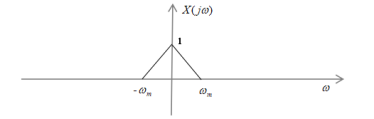
$\begin{align*} X_{s}(j\omega )&=\boldsymbol{F}(x_{s}(t))\\ &=\frac{1}{2 \pi}X(j\omega )*\delta _{\omega _{s}}(\omega )\\ &=\frac{1}{2 \pi}X(j\omega )*\omega _{s}\sum_{n=-\infty }^{+\infty }\delta (\omega -n\omega _{s})\overset{{\color{Red} 1}}{\leftarrow}\\ &=\frac{1}{T}\sum_{n=-\infty }^{+\infty }X(j(\omega - n\omega _{s})) \overset{{\color{Red} (1)}}{\leftarrow} \end{align*}$

假设x(t)为带限信号， $X(j\omega )$ 、 $X_{s}(j\omega )$ 频谱示意图如下：

根据周期冲激信号的定义以及冲激信号的筛选特性：

$x_{s}(t)=x(t)\delta _{T}(t)=x(t)\sum_{k=-\infty }^{+\infty }\delta (t-kT)=\sum_{k=-\infty }^{+\infty }x(kT)\delta (t-kT)$

对其进行连续时间Fourier变换：

$\begin{align*} X_{s}(j\omega ) &= \int_{-\infty }^{+\infty }x_{s}(t)e^{-j\omega t}dt\\ &= \int_{-\infty }^{+\infty }\sum_{k=-\infty }^{+\infty }x(kT)\delta (t-kT)e^{-j\omega t}dt\\ &= \int_{-\infty }^{+\infty }\sum_{k=-\infty }^{+\infty }x(kT)\delta (t-kT)e^{-j\omega kT}dt\\ &=\sum_{k=-\infty }^{+\infty }x[k]e^{-j\omega kT}\\ &=\sum_{k=-\infty }^{+\infty }x[k]e^{-j\Omega k},\,\, \Omega =\omega T\overset{{\color{Red} (2)}}{\leftarrow}\\ &=X(e^{j\Omega }) \end{align*}$

结论：

1、由式子(2)可以看出，抽样信号 $x_{s}(t)$ 频谱 $X_{s}(j\omega )$ 是连续信号 $x(t)$ 频谱 $X(j\omega )$ 的周期性搬移，幅度为原来的 $\frac{1}{T}$ 。即时域离散化对应频域周期化，反过来亦成立，频域离散化时域周期化。

2、式子②中， $\Omega = \omega T = \frac{\omega }{f_{s}}$ 揭示了连续时间信号与离散时间信号的内在关系，架起了连续时间信号与离散时间信号相互转换的桥梁。

3、当 $\Omega = \omega T = \frac{\omega }{f_{s}}$ 时，实际抽样信号 $x_{s}(t)$ 的连续时间Fourier变换近似于理想离散信号 $x[k]$ 的DTFT。

4、从 $X_{s}(j\omega )$ 频谱图可以看到，对最高角频率为 $\omega _{m}$ 的带限信号进行时域抽取，为了防止抽样信号出现频谱混叠，需要满足Nyquist采样定理，即 $\omega _{s}\geqslant 2\omega _{m} \Leftrightarrow f_{s}\geqslant 2f_{m} \Leftrightarrow T\leqslant \frac{1}{2f_{m}}$

5、在实际工程中，很多信号的频谱很宽或无限宽，不满足时域抽样定理，若直接对其进行抽样，将产生无法接受的频谱混叠（称为混叠误差）。为了改善这种情况，对待抽样的连续信号先进行低通滤波，使之变为带限信号，再对其进行抽样，从而减少频谱混叠。这类低通滤波器称为抗混叠滤波器，信号经过抗混叠滤波器后会损失一些信息（称为截短误差），但在大多数场合下，截短误差远远小于混叠误差。

2.信号重建

将离散信号转换为连续信号的过程称为信号重建，其为信号时域抽样的逆过程。

信号的重建可以分为两个过程：首先是将离散时间信号 $x[k]$ 转换为连续时间信号 $x_{rec}(t)$ ，然后将信号 $x_{rec}(t)$ 通过一个截止频率为 $\frac{2}{\omega _{s}}$ 的理想低通滤波器 $H_{rec}(j\omega )$ 。

连续时间信号 $x_{rec}(t)$ 表达式： $x_{rec}(t)=\sum_{k=-\infty }^{+\infty }x[k]\delta (t-kT)$

由时域抽样定理的证明过程可知， $x_{rec}(t)$ 的连续时间Fourier变换为：

$X_{rec}(j\omega )=\frac{1}{T}\sum_{n=-\infty }^{+\infty }X(j(\omega -n\omega )),\, \,\, \omega _{s}=\frac{2\pi}{T}$

若 $x[k]$ 为带限信号， $x_{rec}(t)$ 的频谱示意图如下：

将连续信号 $x_{rec}(t)$ 通过截止频率为 $\omega _{c} = \frac{\omega _{s}}{2}=\frac{\pi}{T}$ 的理想低通滤波器 $H_{rec}(j\omega )$ （成为重建滤波器），即可恢复抽样前的连续信号 $x(t)$ 。

理想低通滤波器频率响应:

$H_{rec}(j\omega ) = \left\{\begin{matrix} T ,\, \, \left | \omega \right | \leqslant \frac{\omega _{s}}{2}\\ 0 ,\, \,\, \left | \omega \right | \geqslant \frac{\omega _{s}}{2} \end{matrix}\right.$

对 $H_{rec}(j\omega )$ 进行连续时间Fourier逆变换得到 $h_{rec}(t)=Sa(\frac{\pi}{T}t)$

信号重建的输出信号 $x(t)$ 与输入信号 $x[k]$ 之间的关系可表示为：

$\begin{align*} x(t) &= x_{rec}(t)*h_{rec}(t)\\ &=\left [ \sum_{k=-\infty }^{+\infty }x[kT]\delta (t-kT) \right ]*Sa(\frac{\pi}{T}t)\\ &= \sum_{k=-\infty }^{+\infty }x[k]Sa(\frac{\pi}{T}(t-kT)) \end{align*}$

3.频域抽样定理推导

对于非周期序列 $x[k]$ 的频谱 $X(e^{j\Omega })$ 都是周期为 $2\pi$ 的连续函数，故只需讨论在一个周期 $\left [ 0,\, 2\pi \right ]$ 内的抽样情况。对 $X(e^{j\Omega })$ 以 $\Omega _{0}=\frac{2\pi}{N}$ (N为一个周期内的抽样点数)等间隔抽样，得到周期序列 $\tilde{X}[m]$ 。

即 $\tilde{X}[m] = X(e^{j\Omega })|_{\Omega =\frac{2\pi}{N}m}=\sum_{n=-\infty }^{+\infty }x[n]e^{-j\Omega n}|_{\Omega =\frac{2\pi}{N}}=\sum_{n=-\infty }^{+\infty }x[n]e^{-j\frac{2\pi}{N}m}$

令 $n=k+rN,\, \, k=0,1...,N-1,\, \, r\in Z$

则有

$\begin{align*} \tilde{X}[m] &= \sum_{k=0}^{N-1}\sum_{r=-\infty }^{+\infty }x[k+rN]e^{-j\frac{2\pi}{N}m(k+rN)}\\ &= \sum_{k=0}^{N-1}(\sum_{r=-\infty }^{+\infty }x[k+rN])e^{-j\frac{2\pi}{N}mk}\\ &= \sum_{k=0}^{N-1}\tilde{x}_{N}[k]e^{-j\frac{2\pi}{N}mk} \end{align*}$

结论：

1、如果 $\tilde{X}[m]$ 是 $X(e^{j\Omega })$ 的等间隔( $\Omega _{0}=\frac{2\pi}{N}$ )抽样，则 $\tilde{X}[m]$ 对应的时域序列 $\tilde{x}_{N}[k]$ 为 $X(e^{j\Omega })$ 对应的时域序列 $x[k]$ 的周期化，周期为 $N$ 。

2、当 $x[k]$ 是长度为 $L$ 的有限长序列，且满足 $L\leqslant N$ 时，周期化的过程中没用发生混叠。当 $x[k]$ 是无限长序列时，或者有限长序列 $x[k]$ 的长度 $L > N$ 时，则在周期化的过程中，序列 $x[k]$ 的非0样本点将会重叠。

4.注释解析

注释1：

周期冲激信号： $\delta _{T}(t) = \sum_{n=-\infty }^{+\infty }\delta (t+nT)$

对于任意的周期信号都可以用傅里叶级数形式表示：

$f(t)=\sum_{n=-\infty }^{+\infty }C_{n}e^{jn\omega_{0} t}\\$ 其中 $C_{n}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\omega_{0} t}dt$

则有：

$C_{n}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\delta _{T}(t)e^{-jn\omega_{0} t}dt=\frac{1}{T}$

$\delta _{T}(t) = \sum_{n=-\infty }^{+\infty }\frac{1}{T}e^{jn\omega_{0} t}$

对周期冲激信号进行连续时间Fourier变换：

$\begin{align*} \delta _{\omega _{s}} &= \boldsymbol{F}(\delta _{T}(t))\\ &= \int_{-\infty }^{+\infty }\sum_{n=-\infty }^{+\infty }\frac{1}{T}e^{jn\omega _{0}t}\, e^{-j\omega t}dt\\ &=\frac{1}{T}2\pi\sum_{n=-\infty }^{+\infty }\delta (\omega -n\omega _{0})\\ &=\omega _{s}\sum_{n=-\infty }^{+\infty }\delta (\omega -n\omega _{s}) \end{align*}$