高效微调大模型：LoRA技术详解

LoRA（Low-Rank Adaptation）是一种用于微调大型预训练模型的技术，旨在高效地适应特定任务，同时减少计算和存储开销。

预训练模型：如DeepSeek、BERT、GPT等，已在大量数据上训练，具备广泛的语言理解能力。

微调：为适应特定任务，通常需要对整个模型进行微调，但这种方法计算和存储成本高。

 

 

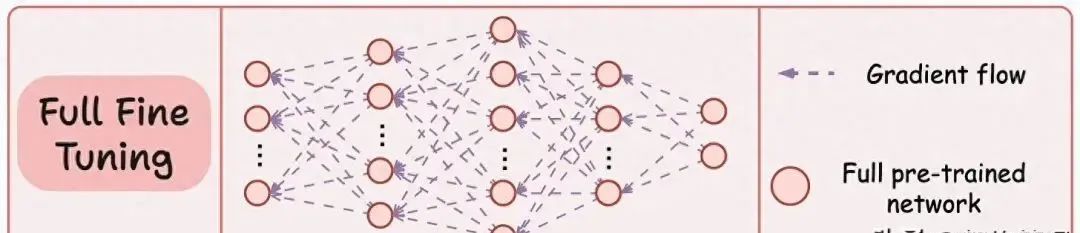
虽然这种微调技术已经成功使用了很长时间，但在用于更大的模型时——例如大语言模型（LLM），就会出现问题，主要因为：

• 模型的大小。

• 微调所有权重的成本。

• 维护所有微调后的大模型的成本。

LoRA 微调解决了传统微调的局限性。

1.LoRA的核心思想

核心思想是将原始模型的权重矩阵（部分或全部）分解为低秩矩阵，并训练这些矩阵。

只更新少量参数，而不是整个模型，从而减少计算和存储需求。

如图所示，底部网络表示大型预训练模型，而顶部网络表示带有 LoRA 层的模型。

 

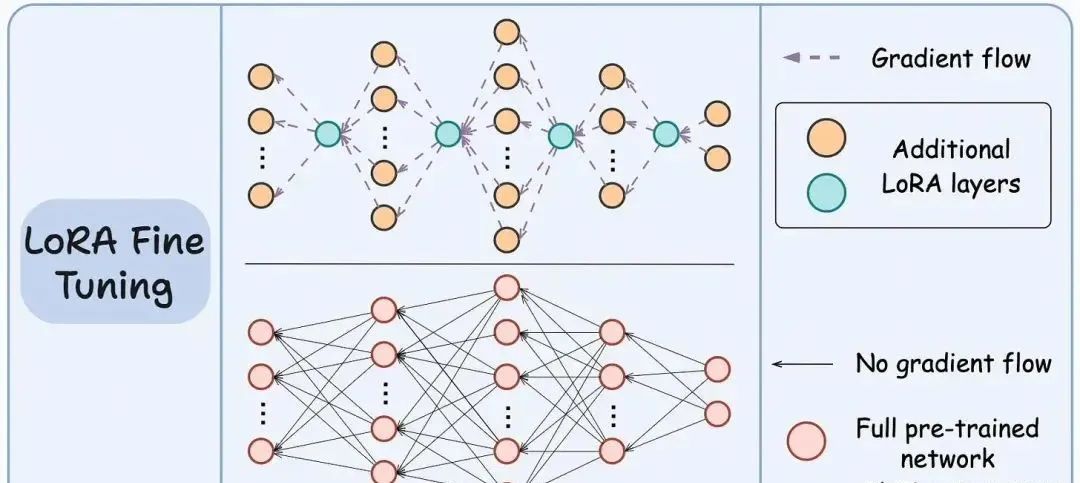
其核心思想是只训练 LoRA 网络，而冻结大型模型。

2.实现步骤

冻结预训练模型：保持大部分参数不变。

引入低秩矩阵：在关键层（如注意力机制）添加低秩矩阵，用于捕捉任务特定的变化。

微调低秩矩阵：只训练这些低秩矩阵，保持原始模型参数不变。

对于需要微调的模型中的某些线性层（例如注意力层或全连接层），LoRA方法冻结原始权重，并引入两个低秩矩阵A和B，使得模型最终使用的权重可以表示为：

 W_effective = W + ΔW, 其中 ΔW = A × B

这里A和B的秩非常小（例如秩r远小于输入和输出维度），因此只需训练这两个低秩矩阵而非整个权重矩阵。

 

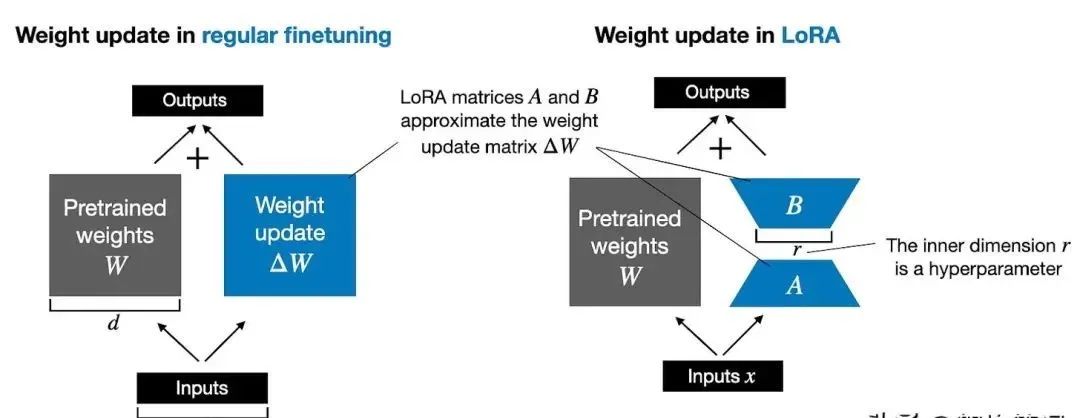
LoRA微调通过这种增量调整方式，既保留了预训练模型的强大表达能力，又实现了在新任务上的高效适应，是当前大模型微调领域非常流行的技术之一。

3.理解矩阵的秩

在线性代数中，矩阵的秩（Rank）是指矩阵中线性无关的行或列的最大数目。一个矩阵的秩不会超过其行数或列数的最小值。秩反映了矩阵的信息量和独立性。

例如，对于一个 m×n 的矩阵：

• 如果其秩为 r，则说明矩阵中存在 r 个线性无关的行（或列）。

• 秩反映了矩阵的“有效维度”，低秩通常意味着矩阵的数据存在冗余，许多行或列可以通过其他行或列的线性组合来表示。

在许多应用中，例如数据降维、低秩分解或模型压缩中，都利用这一性质简化问题和减少参数。