threejs几何体BufferGeometry顶点

1. 几何体顶点位置数据和点模型

本章节主要目的是给大家讲解几何体geometry的顶点概念,相对偏底层一些，不过掌握以后，你更容易深入理解Threejs的几何体和模型对象。

缓冲类型几何体BufferGeometry

threejs的长方体BoxGeometry、球体SphereGeometry等几何体都是基于BufferGeometry (opens new window)类构建的，BufferGeometry是一个没有任何形状的空几何体，你可以通过BufferGeometry自定义任何几何形状，具体一点说就是定义顶点数据。

//创建一个空的几何体对象
const geometry = new THREE.BufferGeometry(); 

BufferAttribute定义几何体顶点数据

通过javascript类型化数组 (opens new window)Float32Array创建一组xyz坐标数据用来表示几何体的顶点坐标。

//类型化数组创建顶点数据
const vertices = new Float32Array([0, 0, 0, //顶点1坐标50, 0, 0, //顶点2坐标0, 100, 0, //顶点3坐标0, 0, 10, //顶点4坐标0, 0, 100, //顶点5坐标50, 0, 10, //顶点6坐标
]);

通过threejs的属性缓冲区对象BufferAttribute (opens new window)表示threejs几何体顶点数据。

// 创建属性缓冲区对象
//3个为一组，表示一个顶点的xyz坐标
const attribue = new THREE.BufferAttribute(vertices, 3); 

设置几何体顶点.attributes.position

通过geometry.attributes.position设置几何体顶点位置属性的值BufferAttribute。

// 设置几何体attributes属性的位置属性
geometry.attributes.position = attribue;

 点模型Points

点模型Points (opens new window)和网格模型Mesh一样，都是threejs的一种模型对象，只是大部分情况下都是用Mesh表示物体。

网格模型Mesh有自己对应的网格材质，同样点模型Points有自己对应的点材质PointsMaterial

// 点渲染模式
const material = new THREE.PointsMaterial({color: 0xffff00,size: 10.0 //点对象像素尺寸
}); 

几何体geometry作为点模型Points参数，会把几何体渲染为点，把几何体作为Mesh的参数会把几何体渲染为面。

const points = new THREE.Points(geometry, material); //点模型对象

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 数组里面编写顶点的坐标数据0, 0, 0, //顶点1坐标50, 0, 0, //顶点2坐标0, 100, 0, //顶点3坐标0, 0, 10, //顶点4坐标0, 0, 100, //顶点5坐标50, 0, 10, //顶点6坐标
])
// BufferAttribute属性缓冲对象表示顶点数据
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attribute// 点材质
const material = new THREE.PointsMaterial({color: 0xffff00,size: 10
})
// 定义了一个点模型对象
const points = new THREE.Points(geometry,material)
export default points

2. 线模型对象

线模型Line渲染顶点数据

下面代码是把几何体作为线模型Line (opens new window)的参数，你会发现渲染效果是从第一个点开始到最后一个点，依次连成线。

// 线材质对象
const material = new THREE.LineBasicMaterial({color: 0xff0000 //线条颜色
}); 
// 创建线模型对象
const line = new THREE.Line(geometry, material);

 效果：

线模型LineLoop、LineSegments

threejs线模型除了Line，还提供了LineLoop (opens new window)、LineSegments (opens new window)，区别在于绘制线条的规则不同。

// 闭合线条
const line = new THREE.LineLoop(geometry, material); 

 

//非连续的线条
const line = new THREE.LineSegments(geometry, material);

 

代码：

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 数组里面编写顶点的坐标数据0, 0, 0, //顶点1坐标50, 0, 0, //顶点2坐标0, 100, 0, //顶点3坐标0, 0, 10, //顶点4坐标0, 0, 100, //顶点5坐标50, 0, 10, //顶点6坐标
])
// BufferAttribute属性缓冲对象表示顶点数据
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attribute// 点材质
const material = new THREE.LineBasicMaterial({color: 0xffff00, //黄色线条
})// 定义了一个线模型对象
// Line 线条
// LineLoop 闭合线条
// LineSegments 非连续的线条
const line = new THREE.LineSegments(geometry,material)
export default line

3. 网格模型(三角形概念)

本节课给大家演示网格模型Mesh渲染自定义几何体BufferGeometry的顶点坐标,通过这样一个例子帮助大家建立**三角形(面)**的概念

三角形(面)

网格模型Mesh其实就一个一个三角形(面)拼接构成。使用网格模型Mesh渲染几何体geometry，就是几何体所有顶点坐标三个为一组，构成一个三角形，多组顶点构成多个三角形，就可以用来模拟表示物体的表面。

网格模型三角形：正反面

正面：逆时针
反面：顺时针
空间中一个三角形有正反两面，那么Three.js的规则是如何区分正反面的？非常简单，你的眼睛(相机)对着三角形的一个面，如果三个顶点的顺序是逆时针方向，该面视为正面，如果三个顶点的顺序是顺时针方向，该面视为反面。

双面可见

Three.js的材质默认正面可见，反面不可见。

const material = new THREE.MeshBasicMaterial({color: 0x0000ff, //材质颜色side: THREE.FrontSide, //默认只有正面可见
});

const material = new THREE.MeshBasicMaterial({side: THREE.DoubleSide, //两面可见
});

const material = new THREE.MeshBasicMaterial({side: THREE.BackSide, //设置只有背面可见
});

代码：

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 数组里面编写顶点的坐标数据0, 0, 0, //顶点1坐标50, 0, 0, //顶点2坐标0, 100, 0, //顶点3坐标0, 0, 10, //顶点4坐标0, 0, 100, //顶点5坐标50, 0, 10, //顶点6坐标
])
// BufferAttribute属性缓冲对象表示顶点数据
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attribute// 用网格模型mesh渲染自定义的几何体BufferGeometry
const material = new THREE.MeshBasicMaterial({color: 0x00ffff, //黄色线条side: THREE.DoubleSide //双面可见   BackSide 背面可见
})const mesh = new THREE.Mesh(geometry,material)
export default mesh

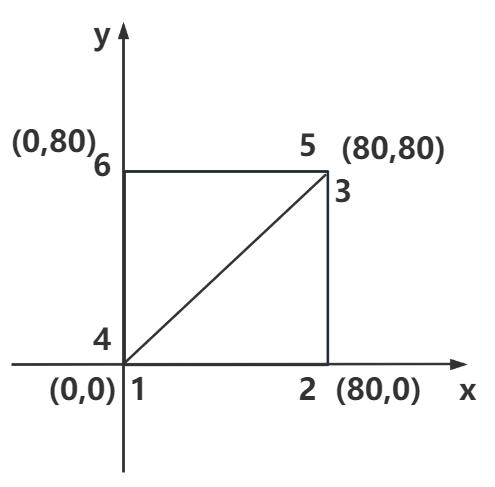
4. 构建一个矩形平面几何体

有了前面几节课，自定义几何体BufferGeometry的基础，你可以尝试自己去构建一个矩形平面几何体。

定义矩形几何体顶点坐标

一个矩形平面，可以至少通过两个三角形拼接而成。而且两个三角形有两个顶点的坐标是重合的。

注意三角形的正反面问题：保证矩形平面两个三角形的正面是一样的，也就是从一个方向观察，两个三角形都是逆时针或顺时针。

const vertices = new Float32Array([0, 0, 0, //顶点1坐标80, 0, 0, //顶点2坐标80, 80, 0, //顶点3坐标0, 0, 0, //顶点4坐标   和顶点1位置相同80, 80, 0, //顶点5坐标  和顶点3位置相同0, 80, 0, //顶点6坐标
]);

 效果：

model.js

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 矩形平面的第一个三角形0, 0, 0, //顶点1坐标80, 0, 0, //顶点2坐标80, 80, 0, //顶点3坐标// 矩形平面的第二个三角形0, 0, 0, //顶点4坐标   和顶点1位置相同80, 80, 0, //顶点5坐标  和顶点3位置相同0, 80, 0, //顶点6坐标
])
// BufferAttribute属性缓冲对象表示顶点数据
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attribute// 用网格模型mesh渲染自定义的几何体BufferGeometry
const material = new THREE.MeshBasicMaterial({color: 0x00ffff, //黄色线条side: THREE.DoubleSide //双面可见   BackSide 背面可见
})const mesh = new THREE.Mesh(geometry,material)
export default mesh

5. 几何体顶点索引数据

网格模型Mesh对应的几何体BufferGeometry，拆分为多个三角后，很多三角形重合的顶点位置坐标是相同的，这时候如果你想减少顶点坐标数据量，可以借助几何体顶点索引geometry.index来实现。

定义顶点位置坐标数据

每个三角形3个顶点坐标，矩形平面可以拆分为两个三角形，也就是6个顶点坐标。

const vertices = new Float32Array([0, 0, 0, //顶点1坐标80, 0, 0, //顶点2坐标80, 80, 0, //顶点3坐标0, 0, 0, //顶点4坐标   和顶点1位置相同80, 80, 0, //顶点5坐标  和顶点3位置相同0, 80, 0, //顶点6坐标
]);

如果几何体有顶点索引geometry.index，那么你可以吧三角形重复的顶点位置坐标删除。

const vertices = new Float32Array([0, 0, 0, //顶点1坐标80, 0, 0, //顶点2坐标80, 80, 0, //顶点3坐标0, 80, 0, //顶点4坐标
]);

BufferAttribute定义顶点索引.index数据

通过javascript类型化数组Uint16Array创建顶点索引.index数据。

// Uint16Array类型数组创建顶点索引数据
const indexes = new Uint16Array([// 下面索引值对应顶点位置数据中的顶点坐标0, 1, 2, 0, 2, 3,
])

 通过threejs的属性缓冲区对象BufferAttribute表示几何体顶点索引.index数据。

// 索引数据赋值给几何体的index属性
geometry.index = new THREE.BufferAttribute(indexes, 1); //1个为一组

代码

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 矩形平面的第一个三角形0, 0, 0, //顶点1坐标  0  索引80, 0, 0, //顶点2坐标  180, 80, 0, //顶点3坐标  2// 矩形平面的第二个三角形// 0, 0, 0, //顶点4坐标   和顶点1位置相同// 80, 80, 0, //顶点5坐标  和顶点3位置相同0, 80, 0, //顶点6坐标  3
])// BufferAttribute属性缓冲对象表示顶点数据
// 这个地方三个表示一个顶点坐标
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attribute// 类型化数组创建顶点数据
const indexes = new Uint16Array([0,1,2,0,2,3
])
// 这个地方，一个索引表示一个顶点坐标
// 几何体顶点索引的定义
geometry.index = new THREE.BufferAttribute(indexes,1)// 用网格模型mesh渲染自定义的几何体BufferGeometry
const material = new THREE.MeshBasicMaterial({color: 0x00ffff, //黄色线条side: THREE.DoubleSide //双面可见   BackSide 背面可见
})const mesh = new THREE.Mesh(geometry,material)
export default mesh

6. 顶点法线数据

前面给大家讲解过几何体顶点位置数据geometry.attributes.position，本节课给大家介绍一种新的顶点数据，就是顶点法线(法向量)数据geometry.attributes.normal。

测试：Basic材质改为Lambert材质

你可以测试下，把前面两节课的案例源码中MeshBasicMaterial材质改为MeshLambertMaterial材质，你会发现原来的矩形平面无法正常渲染，这其实很简单，使用受光照影响的材质，几何体BufferGeometry需要定义顶点法线数据。

// MeshBasicMaterial不受光照影响
// 使用受光照影响的材质，几何体Geometry需要定义顶点法线数据
const material = new THREE.MeshLambertMaterial({color: 0x0000ff, side: THREE.DoubleSide, //两面可见
});

数学上法线概念

先来理解一下数学上的法线概念，比如一个平面，法线的就是该平面的垂线，如果是光滑曲面，一点的法线就是该点切面的法线。

Three.js顶点法线

Three.js中法线和数学中法线概念相似，只是定义的时候更灵活，会根据需要进行调整，作为初学者，只要先有顶点法线的概念就行，下面会举一个简单小例子。

矩形平面几何体法线案例——无顶点索引

Three.js中法线是通过顶点定义，默认情况下，每个顶点都有一个法线数据，就像每一个顶点都有一个位置数据。

// 矩形平面，无索引，两个三角形，6个顶点
// 每个顶点的法线数据和顶点位置数据一一对应
const normals = new Float32Array([0, 0, 1, //顶点1法线( 法向量 )0, 0, 1, //顶点2法线0, 0, 1, //顶点3法线0, 0, 1, //顶点4法线0, 0, 1, //顶点5法线0, 0, 1, //顶点6法线
]);
// 设置几何体的顶点法线属性.attributes.normal
geometry.attributes.normal = new THREE.BufferAttribute(normals, 3); 

练习代码： 

import * as THREE from 'three'
// 创建一个空的几何体顶对象
const geometry = new THREE.BufferGeometry()
// 添加顶点数据
// 类型化数组定义的一组顶点坐标数据
const vertices = new Float32Array([// 矩形平面的第一个三角形0, 0, 0, //顶点1坐标80, 0, 0, //顶点2坐标80, 80, 0, //顶点3坐标// 矩形平面的第二个三角形0, 0, 0, //顶点4坐标   和顶点1位置相同80, 80, 0, //顶点5坐标  和顶点3位置相同0, 80, 0, //顶点6坐标
])
// BufferAttribute属性缓冲对象表示顶点数据
const attribute = new THREE.BufferAttribute(vertices, 3)// 设置几何体的顶点位置属性
geometry.attributes.position = attributeconst normals = new Float32Array([0, 0, 1, //顶点1法向量0, 0, 1, //顶点2法向量0, 0, 1, //顶点3法向量0, 0, 1, //顶点4法向量   和顶点1位置相同0, 0, 1, //顶点5法向量  和顶点3位置相同0, 0, 1, //顶点6法向量
])
// 定义了顶点法线数据或者说顶点法向量数据
geometry.attributes.normal = new THREE.BufferAttribute(normals, 3)// 用网格模型mesh渲染自定义的几何体BufferGeometry
// MeshBasicMaterial
// 不定义法线数据就会无法显示
const material = new THREE.MeshLambertMaterial({color: 0x00ffff, //黄色线条side: THREE.DoubleSide //双面可见   BackSide 背面可见
})const mesh = new THREE.Mesh(geometry,material)
export default mesh

矩形平面几何体法线案例——有顶点索引

// 矩形平面，有索引，两个三角形，有2个顶点重合，有4个顶点
// 每个顶点的法线数据和顶点位置数据一一对应
const normals = new Float32Array([0, 0, 1, //顶点1法线( 法向量 )0, 0, 1, //顶点2法线0, 0, 1, //顶点3法线0, 0, 1, //顶点4法线
]);
// 设置几何体的顶点法线属性.attributes.normal
geometry.attributes.normal = new THREE.BufferAttribute(normals, 3);

7. 查看threejs自带几何体顶点

查看three.js自带几何体顶点结构，基类(父类)BufferGeometry

three.js提供的矩形平面PlaneGeometry、长方体BoxGeometry、球体SphereGeometry等各种形状的几何体，他们都有一个共同的父类BufferGeometry。这意味着这些几何体有哪些属性或方法，你可以查询文档关于BufferGeometry的介绍。

查看几何体顶点位置和索引数据

可以用顶点索引index数据构建几何体，也可以不用，threejs默认的大部分几何体都有三角形的顶点索引数据，具体可以通过浏览器控制台打印几何体数据查看。

const geometry = new THREE.PlaneGeometry(100,50); //矩形平面几何体
// const geometry = new THREE.BoxGeometry(50,50,50); //长方体console.log('几何体',geometry);
console.log('顶点位置数据',geometry.attributes.position);
console.log('顶点索引数据',geometry.index);

材质属性.wireframe

线条模式渲染，查看几何体三角形结构

const material = new THREE.MeshLambertMaterial({color: 0x00ffff, wireframe:true,//线条模式渲染mesh对应的三角形数据
});

几何体细分数

Three.js很多几何体都提供了细分数相关的参数，这里以矩形平面几何体PlaneGeometry为例介绍。

矩形平面几何体至少需要两个三角形拼接而成。

 //矩形几何体PlaneGeometry的参数3,4表示细分数，默认是1,1
const geometry = new THREE.PlaneGeometry(100,50,1,1);

把一个矩形分为2份，每个矩形2个三角形，总共就是4个三角形

const geometry = new THREE.PlaneGeometry(100,50,2,1);

把一个矩形分为4份，每个矩形2个三角形，总共就是8个三角形

const geometry = new THREE.PlaneGeometry(100,50,2,2);

球体SphereGeometry细分数

球体SphereGeometry参数2、3分别代表宽、高度两个方向上的细分数，默认32,16，具体多少以你所用版本为准。

const geometry = new THREE.SphereGeometry( 50, 32, 16 );

如果球体细分数比较低，表面就不会那么光滑。

const geometry = new THREE.SphereGeometry( 15, 8, 8 );

三角形数量与性能

对于一个曲面而言，细分数越大，表面越光滑，但是三角形和顶点数量却越多。

几何体三角形数量或者说顶点数量直接影响Three.js的渲染性能，在不影响渲染效果的情况下，一般尽量越少越好。

代码：

import * as THREE from "three";
// 创建一个空的几何体顶对象
// const geometry = new THREE.BoxGeometry(100,100,100) //长方体
// const geometry = new THREE.PlaneGeometry(100, 100,2,2); //矩形平面
const geometry = new THREE.SphereGeometry(50, 32, 16); //矩形平面
console.log(".position", geometry.attributes.position);
console.log(".index", geometry.index); //36个数据，每个点有三个坐标信息const material = new THREE.MeshLambertMaterial({color: 0x00ffff, //黄色线条wireframe:true,//线条模式渲染mesh对应的三角形数据
});const mesh = new THREE.Mesh(geometry, material);
export default mesh;

8. 旋转、缩放、平移几何体

BufferGeometry通过.scale()、.translate()、.rotateX()、.rotateY()等方法可以对几何体本身进行缩放、平移、旋转,这些方法本质上都是改变几何体的顶点数据。

// 几何体xyz三个方向都放大2倍
geometry.scale(2, 2, 2);
// 几何体沿着x轴平移50
geometry.translate(50, 0, 0);
// 几何体绕着x轴旋转45度
geometry.rotateX(Math.PI / 4);
// 几何体旋转、缩放或平移之后，查看几何体顶点位置坐标的变化
// BufferGeometry的旋转、缩放、平移等方法本质上就是改变顶点的位置坐标
console.log('顶点位置数据', geometry.attributes.position);

缩放.scale()

// 几何体xyz三个方向都放大2倍
geometry.scale(2, 2, 2);// 几何体旋转、缩放或平移之后，查看几何体顶点位置坐标的变化
// BufferGeometry的旋转、缩放、平移等方法本质上就是改变顶点的位置坐标
console.log('顶点位置数据', geometry.attributes.position);

平移.translate()

// 几何体沿着x轴平移50
geometry.translate(50, 0, 0);

旋转.rotateX()、.rotateY()、.rotateZ()

// 几何体绕着x轴旋转45度
geometry.rotateX(Math.PI / 4);

居中.center()

geometry.translate(50, 0, 0);//偏移
// 居中：已经偏移的几何体居中，执行.center()，你可以看到几何体重新与坐标原点重合
geometry.center();

代码：

import * as THREE from "three";
// 创建一个空的几何体顶对象
const geometry = new THREE.PlaneGeometry(100, 100); //矩形平面
// geometry.scale(2, 2, 2); //缩放
geometry.translate(50, 0, 0);
// geometry.rotateX(-Math.PI / 2); //绕x轴旋转90度
// 居中
geometry.center()
console.log(".position", geometry.attributes.position);
// console.log(".index", geometry.index); //36个数据，每个点有三个坐标信息const material = new THREE.MeshLambertMaterial({color: 0x00ffff, //黄色线条// wireframe:true,//线条模式渲染mesh对应的三角形数据side: THREE.DoubleSide, //两面可见
});const mesh = new THREE.Mesh(geometry, material);
export default mesh;