Java语言快速排序和堆排序(优先队列)介绍,附demo代码
快速排序:
快速排序是由东尼·霍尔所发展的一种排序算法,在平均状况下,排序 n 个项目要 Ο(n log n) 次比较。在最坏状况下则需要 Ο(n^2) 次比较,但这种状况并不常见。快速排序使用分治法策略来把一个序列分为两个子序列,从而实现排序。本文将详细介绍如何使用Java实现快速排序算法,包括基础概念、使用方法、常见实践以及最佳实践。
上面的笼统的概念:
简单来说就是对于一组数据:73, 18, 4, 56, 35, 9, 88, 2, 64, 13, 41, 92, 57, 61, 25, 47, 5
我们每次选取一个下标为p的值,然后将小于p的放在左边,大于p的放在右边。
然后左递归 + 有递归就可以了。
代码如下
package org.example;public class QuickSort {public static void sort(int[] arr, int low, int high) {if (low < high) {// 获取第一次分区后的分区点int pi = partition(arr, low, high);// 左递归sort(arr, low, pi - 1);// 右递归sort(arr, pi + 1, high);}}private static int partition(int[] arr, int low, int high) {// 选择最右边的元素作为基准值int pivot = arr[high];//小于基准值的元素的最后位置 //初始化一个不存在的位置int last = low - 1;// 遍历[low,high)区间,将小于基准值的元素放到左边for (int i = low; i < high; i++) {if (arr[i] < pivot) {//维护last变量,可以发现如果所有的值都小于基准值时,那么last == i ;//每存在一个大于的arr[i] > pivot,就会发现 i 比 last 多一。//last++;swap(arr, last, i);}}// 遍历完成后,如果last == i , 则这步没有意义// 如果last < i , 也就是last的位置的下一个位置是大于pivot,则需要交换,// 这样就可以将大于的放在右边了。// 实在不能理解的话你观察for循环,在遍历的同时存在多个大于pivot时//每遇到一个小于的值就会交换这俩个位置,保证大于pivot的值在左边,//然后这里再swap一次将pivot移到中间来就满足pivot左边是小于的,右边是大于的。// 可以发现不存在last > i 的情况,不用考虑swap(arr, last + 1, high);//至于为什么要last + 1;//我们维护的是小于基准值的元素的最后位置,他的下一个位置arr[(last + 1)]> arr[last]//比如假设基准值为 5 ,遍历过后假设 [2,1,3,4,9,6,7,5],//我们只遍历了[2,1,3,4,9,6,7] 这些值后假设出现了上述情况,那么arr[last] == 4// 返回last就出问题了,小于 5 的值 4 跑到了右边,// 返回last + 1 ,就会变成 [2,1,3,4,5,6,7,9] 保证符合左边<5右边>5。所以返回last + 1return last + 1;}//交换数组的俩个下标的位置,在快速排序是将小于基准值放左边去,也就是交换一下private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
} 我觉得非常通俗易懂奥,相比于写俩个while循环的写法更加简洁,理解起来也更加容易
堆
堆是一种特殊的数据结构,本质就是是一种完全二叉树,并且满足堆属性。在Java中,堆在许多算法和数据处理场景中都有广泛应用,例如优先队列的实现、堆排序算法等。本文将详细介绍Java实现堆的过程、常见用法。
对于他的内部其实就是维护了一个完全二叉树,由于是完全二叉树,我们可以利用数组的索引来表示节点之间的关系。对于一个数组 heap,如果节点 i 的索引为 i,那么它的左子节点索引为 2 * i + 1,右子节点索引为 2 * i + 2,父节点索引为 (i - 1) / 2。基于这个原则,难点在于怎么调整堆。
假设有这样一个乱序序列
73, 18, 4, 56, 35, 9, 88
我们一个个insert插入的时候
插入73的过程:

插入18的过程:

插入4的过程:

上面其实都是按完全二叉树的顺序插入,因为没有发生父节点小于字节的情况嘛。
插入56的过程:就发现当前值56大于他的父节点值18,这时候就需要进行交换。

插入35的过程:

插入9的过程,就发现当前值9大于他的父节点值4,这时候就需要进行交换。

插入88的过程:这步发现当前值88大于他的父节点值9,这时候就需要进行交换。

这就是建堆的过程,写一遍就能感觉很简单了。
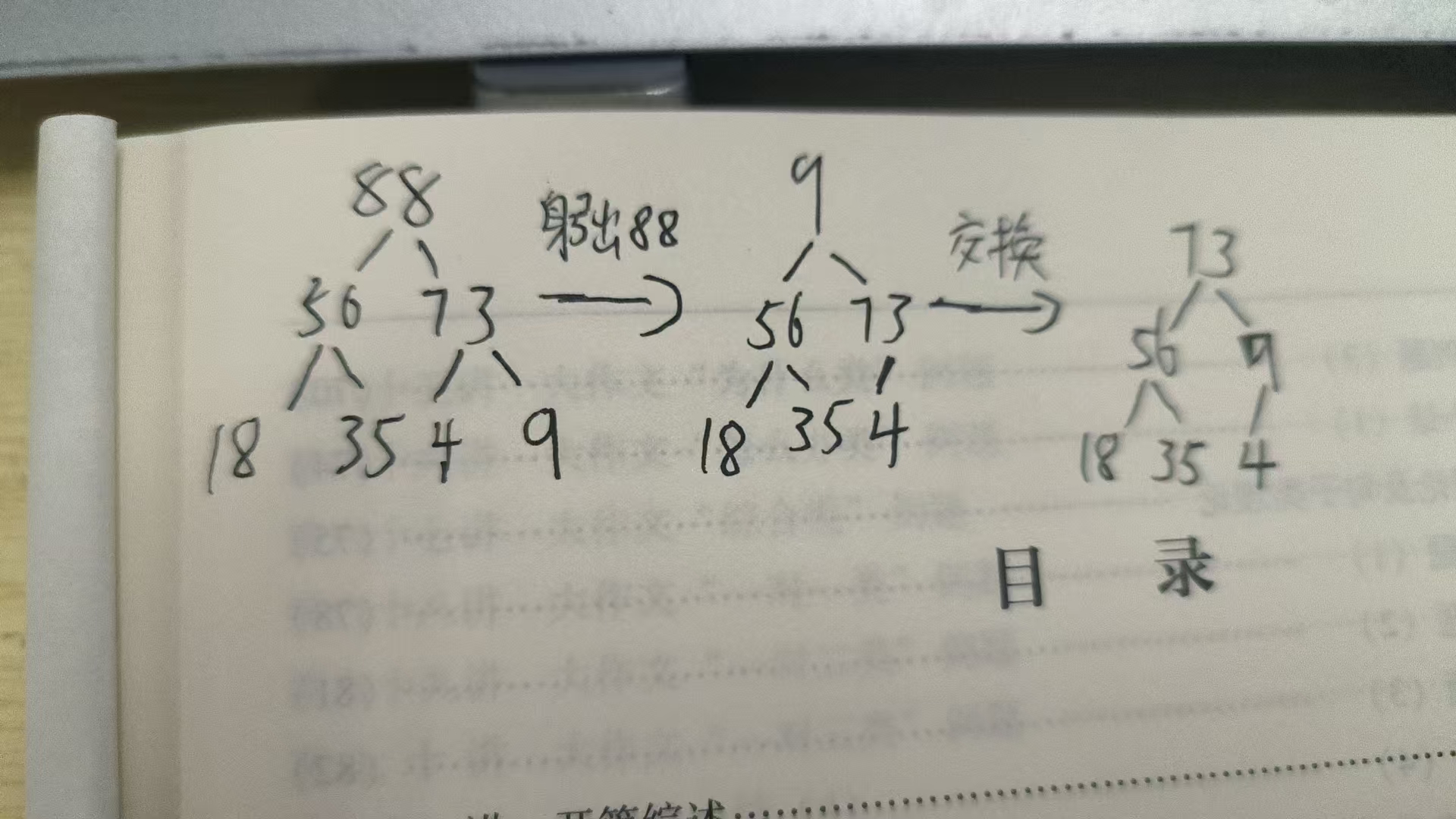
下面讲解每次弹出最大值的过程:
也是按照上面的那个二叉树的逻辑
弹出88是,
package org.example;public class MaxHeap {//数组实现private int[] heap;//当前数组大小private int size;//可接受的最大容量private int capacity;//默认参数设置(capacity = 10)public MaxHeap(){this.capacity = 10;this.size = 0;this.heap = new int [capacity];}//自定义容量设置public MaxHeap(int capacity) {this.capacity = capacity;this.size = 0;this.heap = new int[capacity];}//获取当前数组大小public int getSize() {return size;}// 获取父节点的索引private int parent(int index) {return (index - 1) / 2;}// 获取左子节点的索引private int leftChild(int index) {return 2 * index + 1;}// 获取右子节点的索引private int rightChild(int index) {return 2 * index + 2;}// 交换数组的两个元素private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}// 插入元素(难点)public void insert(int element) {if (size == capacity) {throw new IndexOutOfBoundsException("Heap is full");}heap[size] = element;size++;//需要向下调整堆heapifyUp(size - 1);}// 向上调整堆private void heapifyUp(int index) {//如果当前节点大于父节点的值,就交换一下,一直遍历到小于父节点while (index > 0 && heap[parent(index)] < heap[index]) {swap(parent(index), index);index = parent(index);}}// 获取最大值public int getMax() {if (size == 0) {throw new IndexOutOfBoundsException("Heap is empty");}return heap[0];}// 删除最大值public int deleteMax() {if (size == 0) {throw new IndexOutOfBoundsException("Heap is empty");}int max = heap[0];//将最右下角的值(也就是数组的最后一个值)给移动到根节点,然后删除这个右下角的节点heap[0] = heap[size - 1];size--;//需要向下调整,因为最右下角的值,不一定是最大的,需要重新调整二叉树的结构heapifyDown(0);return max;}// 向下调整堆//采用递归调用的方式调整private void heapifyDown(int index) {//从根节点开始,每次判断左右子节点大小,与最大的进行交换//还需要判断是否到叶子节点了,如果到了叶子节点也就没必要判断了//根节点int largest = index;//左节点int left = leftChild(index);//右节点int right = rightChild(index);//判断左节点是否大于if (left < size && heap[left] > heap[largest]) {largest = left;}//判断右节点大小if (right < size && heap[right] > heap[largest]) {largest = right;}//判断是否到叶子节点了,如果到了叶子节点也就没必要判断了if (largest!= index) {swap(index, largest);heapifyDown(largest);}}
}
归并排序:
合并操作是归并排序中的关键步骤。它将两个已经排序的子数组合并成一个更大的有序数组。在合并过程中,通过比较两个子数组的元素,将较小的元素依次放入结果数组中,直到其中一个子数组的元素全部被处理完,然后将另一个子数组剩余的元素直接追加到结果数组的末尾
简单来说:
对于16 ,15,8,2,11,6,3,10,5,7,1,13,12,4,9,14
先进行拆分
第一次拆分为16,15,8,2,11,6 ,3,10 和 5,7,1,13,12,4,9,14
第二次拆分为:
16,15,8,2
11,6,3,10
5,7,1,13
12,4,9,14
第三次拆分
16,15
8,2
11,6
3,10
5,7
1,13
12,4
9,14
此时每部分数组长度都是2,内部直接返回就行。总体来说就是分治思想。分治思想是归并排序的核心。“分”就是将一个大问题分解成若干个规模较小、相互独立且与原问题形式相同的子问题。“治”则是对这些子问题分别进行求解,然后将子问题的解合并成原问题的解。
import java.util.Arrays;public class MergeSort {public static void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int mid = arr.length / 2;int[] left = Arrays.copyOfRange(arr, 0, mid);int[] right = Arrays.copyOfRange(arr, mid, arr.length);//继续分半,直到数量大小 <= 1mergeSort(left);mergeSort(right);//此时将左数组和右边数组合并,可以保证左数组和右数组都是有序的merge(arr, left, right);}//其实就是合并俩个有序数组,双指针就可以了。不多解释了private static void merge(int[] arr, int[] left, int[] right) {int i = 0, j = 0, k = 0;while (i < left.length && j < right.length) {if (left[i] <= right[j]) {arr[k++] = left[i++];} else {arr[k++] = right[j++];}}while (i < left.length) {arr[k++] = left[i++];}while (j < right.length) {arr[k++] = right[j++];}}
}