【基础算法】二分算法详解
🎯 前言:二分不是找某个数,而是找一个满足条件的位置/值
所以最关键的是:找到单调性,写好 check() 函数,剩下交给模板!
什么是二分算法
二分算法是一种在有序区间中查找答案的方法,时间复杂度:O(log n)。核心思想是:
- 每次把搜索区间分成两半,只保留可能存在答案的那一半,直到找到目标或搜索区间为空。
二分算法的种类
常见的二分算法就只有两种:
- 经典二分 (二分搜索)
- 二分答案 (二分答案 + check)
使用二分的特征 && 使用二分的条件
✨有序就能二分,单调就能逼近 (总结这一块,爆爆的)
使用二分的条件
使用二分需要问题的解具有“二段性”(True/False分界):
若某个值满足条件,则所有更大的值也满足(或反之)
这时就可以用二分在这个“分界点”上逼近最优解。
这个二段性可以理解成单调性,也就是可以将结果以目标值为界限分割成两段,一段大于等于target,另一段小于target;或者一段大于target,另一段小于等于target。具体根据题目要求来规划。
使用二分的特征
如何判断一个问题是否需要二分算法来解决,这也是初学者最关心的问题。
- 查找某个数是否存在
- 查找第一个/最后一个符合条件的位置
- 在问题的答案具有“二段性”时,搜索最优解
这类题目通常是求:最小值、最大值、最短时间、最小代价……
而且我们不难发现,这类问题的某些条件之间是有相互制约的线性关系的,比如某个变量随另一个变量的增长而增长,
于是在这道题的“解空间”中,整道题的答案序列是具有“二段性”的。
二分模板
二分查找 符合条件的区间 的左端点(起始位置)
给出条件:整个序列长度为 n (1-based序列)。
二段性体现:整个序列被分为 >= t 和 < t 两部分。
要查找 >= t 的最小值,也就是查找 >= t 区间的左端点。
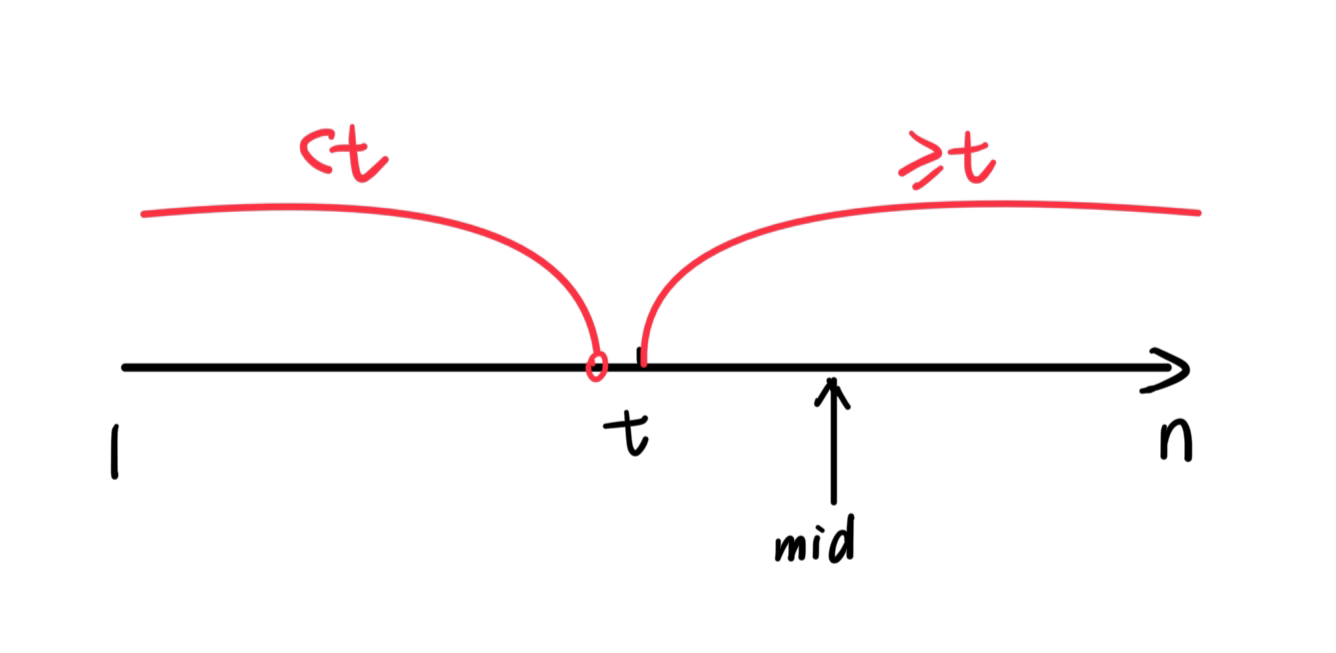
整个查找过程是怎样的呢?先根据 l 和 r 求出中间值 mid,判断 mid 和 t 的大小关系(二分答案就是通过 check 函数去判断 mid 所指向的位置在线性关系中的值与 t 的大小关系)
- 如果 >= t 那么 mid (二分答案就是 check(mid) ) 就落在 >= t 的区间上,下一步就是调整 r 的位置,缩小范围进一步查找。因为此时 mid 指向的位置可能是结果,所以就将 r 调整到 mid 的位置。
- 如果 < t 那么 mid (二分答案就是 check(mid) ) 就落在 < t 的区间上,下一步就是调整 l 的位置,缩小范围进一步查找。此时 mid 指向的位置不可能是结果,因为 < t 区间是取不到 t 的,所以即使 l 在及其靠近 t 的位置,也取不到 t ,那么我们就可以将 l 更新到 mid + 1 的位置。 mid + 1 的位置有可能是结果。
int l = 1, r = n;
while(l < r)
{int mid = (l + r) / 2;if(check(mid)) r = mid;else l = mid + 1;
}
//二分结束之后还需要判断结果是否存在,如果存在,二分停下的位置就是结果
二分查找 符合条件的区间 的右端点(终止位置)
查找中止位置,要找的就是 <= t 的区间的右端点
注意!!!找右端点时要注意求中间值是要+1的
小窍门:也可以先分析出l、r是怎么更新的,然后看l、r的更新有没有出现 -1,如果出现了 -1,求中间值时就要 +1 中和一下。
int l = 1, r = n;
while(l < r)
{int mid = (l + r + 1) / 2; //注意这里求中间值是要+1的if(check(mid)) l = mid;else r = mid - 1;
}
//别忘了判断结果
二分细节处理
细节部分想知道为什么会进入死循环的自己举个简单的例子画图理解就能明白了。我懒得画了。。。
求中间值
对于中间值 mid 的计算方式是有两种的:
int mid = (l + r) / 2;当序列个数是偶数个时,得到中点位于中间偏左;奇数个均相同。int mid = (l + r + 1) / 2;当序列个数是偶数个时,得到中点位于中间偏右
在找起始位置的时候,求中间值要用方式1,用方式2会死循环。
在找中止位置的时候,求中间值要用方式2,用方式1会死循环。
求中间值防溢出写法
int mid = l + (r - l) / 2;中间偏左int mid = l + (r - l + 1) / 2;中间偏右
循环条件
对于循环条件,无论是求起始位置还是求中止位置,统一要使用while(l < r),而不能写成while(l <= r),这样会死循环。
二分答案
通过题目来理解二分答案
P2440 木材加工
洛谷:P2440 木材加工

分析
这道题目难的在于思路,我们根据题意可得:木头切割的段数 k 和每段小木头的长度 l 是存在反比关系的。题目要求没小段木头的长度越大越好,并且要求出最大的长度,但是题目同时又给出了需要得到小段木头的数量。那么此时,题目就变成了在解空间有“二段性”的性质下,求最大值的问题。那么这题就是很明显的二分答案。ps:你总不能是看到我二分答案的tag就知道这题要用二分答案吧🤡。
其实这题我刚开始看到想到的是直接从大到小枚举所有的长度,但是分析数据范围就知道,暴力枚举肯定是超时的。于是在此基础上我们就要想优化办法,于是才得到的二分方案。解题思路是有个分析过程的,从暴力到优化。
