「HHT(希尔伯特黄变换)——ECG信号处理-第十三课」2025年5月19日
一、引言
心电信号(ECG)是反映心脏电活动的重要生理信号,其特征提取对于心脏疾病的诊断和监测具有关键意义。Hilbert - Huang Transform(HHT)作为一种强大的信号处理工具,在心电信号特征提取领域得到了广泛应用。本文将深入解析HHT在心电信号特征提取中的应用原理、优势以及实际操作步骤,帮助读者更好地理解和应用这一技术。
二、HHT基本原理
2.1 经验模态分解(Empirical Mode Decomposition,EMD)
经验模态分解(Empirical Mode Decomposition,EMD)是HHT的核心部分,它能够将复杂的非平稳信号分解为若干个本征模态函数(Intrinsic Mode Functions,IMFs)。IMFs反映了信号在不同时间尺度上的局部特征。EMD分解过程是基于信号的局部极值点,通过不断筛选出信号中的局部极值点来构造上下包络线,从而得到各个IMFs。这一过程是自适应的,不需要预先设定信号的模型,能够很好地适应心电信号的非平稳特性。

图1 经验模态分解示意图
2.1.1. IMF的定义
一个本征模态函数(IMF)必须满足以下两个条件:
-
在整个数据段内,极值点(极大值点和极小值点)的数量和过零点的数量必须相等,或者最多相差一个。
-
在任意时刻,由局部极大值点定义的上包络和由局部极小值点定义的下包络的平均值为零。
2.1.2 EMD分解步骤
EMD分解过程可以分为以下几个步骤:
(1)寻找局部极值点
-
对于给定的信号 s(t),首先找到所有的局部极大值点和极小值点。局部极大值点是指在该点及其邻域内,信号值达到局部最大值;局部极小值点是指在该点及其邻域内,信号值达到局部最小值。
(2)构造上下包络线
- 使用三次样条插值方法,通过局部极大值点构造上包络线 Eupper(t),通过局部极小值点构造下包络线 Elower(t)。包络线的构造公式如下:


(3)计算均值
-
计算上下包络线的均值 m(t):

(4)筛选过程
-
从原始信号中减去均值 m(t),得到新的信号 h(t):
![]()
-
检查 h(t) 是否满足IMF的条件。如果满足,则 h(t) 是一个IMF;如果不满足,则将 h(t) 作为新的信号,重复上述步骤,直到满足IMF的条件。
(5)分解IMFs
-
重复上述过程,从原始信号中逐步提取出各个IMF。每次提取一个IMF后,从原始信号中减去该IMF,得到剩余信号,然后对剩余信号继续进行EMD分解,直到剩余信号不再包含任何IMF为止。
2.1.3 EMD分解的数学表示
假设原始信号为 s(t),通过EMD分解可以得到 n 个IMF和一个残差 r(t):
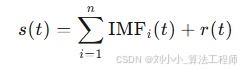
其中,IMFi(t) 表示第 i 个本征模态函数,r(t) 是分解后的残差,包含信号的低频趋势或噪声成分。
2.2 Hilbert变换
Hilbert变换用于将每个IMF转换为解析信号,从而得到信号的瞬时频率和瞬时幅值。解析信号的实部是原始信号,虚部是通过Hilbert变换得到的信号。通过解析信号可以计算得到瞬时频率和瞬时幅值。在心电信号中,瞬时频率可以反映心率的变化情况,例如在心房纤颤时,心率会变得不规则,瞬时频率会出现较大的波动。瞬时幅值则可以反映信号的强度变化,对于检测心肌梗死等导致信号幅度变化的疾病具有重要意义。

图2 希尔伯特-黄变换示意图(信号分解为瞬时频率和瞬时振幅)
2.2.1 Hilbert变换的定义
对于一个实值信号 x(t),其Hilbert变换 x^(t) 定义为:

解析信号 z(t) 可以表示为:
![]()
其中,j 是虚数单位。
2.2.2 瞬时频率和瞬时幅值的计算
解析信号 z(t) 可以表示为:
![]()
其中,A(t) 是瞬时幅值,ϕ(t) 是瞬时相位。瞬时频率 ω(t) 可以通过瞬时相位的导数得到:

瞬时幅值 A(t) 和瞬时相位 ϕ(t) 的计算公式分别为:

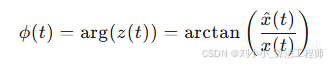
2.2.3 HHT的完整流程
HHT的完整流程可以总结为以下步骤:
-
EMD分解:将原始信号 s(t) 分解为若干个IMFs和一个残差 r(t)。
-
Hilbert变换:对每个IMF进行Hilbert变换,得到解析信号。
-
特征提取:通过解析信号计算瞬时频率和瞬时幅值,提取信号的特征。
三、HHT在心电信号特征提取中的应用
3.1 实验过程
通过对心电信号进行EMD分解,我们得到了多个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。以下是具体的实验结果和分析:
(1)原始心电信号
-
图3展示了原始心电信号的波形,可以看出心电信号的周期性和波动性。

图3 原始心电信号(mitdb-222号记录)
(2)EMD分解结果
-
图4展示了EMD分解后的10个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。

图4 EMD分解(mitdb-222号记录)
-
图5展示了EMD分解结果的小窗显示,通过偏移量区分不同的IMF,便于观察和比较。

图5 EMD分解的偏移量小窗显示(mitdb-222号记录)
(3)IMF的瞬时频率
-
图6展示了某个IMF的瞬时频率。瞬时频率的变化可以反映心电信号的动态特性,有助于识别心电信号中的异常特征。

图6 IMF2的瞬时频率(mitdb-222号记录)
(4)统计学显著性检验
在 HHT(希尔伯特-黄变换)中,显著性检验的结果可以帮助我们判断通过 EMD 分解得到的固有模态函数(IMF)是否具有统计学上的显著性。具体来说,显著性检验的结果可以帮助我们区分哪些 IMF 是由信号的真实特征引起的,哪些是由噪声引起的。
显著性检验的目的是评估 IMF 的能量分布是否显著不同于白噪声的能量分布。具体步骤如下:
-
EMD 分解:对心电信号进行 EMD 分解,得到多个 IMF。
-
计算显著性线:计算这些 IMF 的能量分布,并确定在特定置信水平(如 95% 和 99%)下的显著性线。
-
能量分布图:绘制能量分布图,将实际信号的 IMF 能量分布与显著性线进行比较。(95% 显著性线:表示在 95% 的置信水平下,IMF 能量分布的上限。99% 显著性线:表示在 99% 的置信水平下,IMF 能量分布的上限。能量分布点:表示实际信号的 IMF 能量分布的对数值。)
-
显著性判断:
-
如果某个 IMF 的能量分布点超出了 99% 显著性线(上方),那么这个 IMF 在 99% 的置信水平下是显著的,可以认为它是由信号的真实特征引起的。
-
如果某个 IMF 的能量分布点超出了 95% 显著性线但未超出 99% 显著性线,那么这个 IMF 在 95% 的置信水平下是显著的,但在 99% 的置信水平下不显著。
-
如果某个 IMF 的能量分布点未超出 95% 显著性线(上方),那么这个 IMF 在 95% 的置信水平下也不显著,可以认为它主要是由噪声引起的。
-
-
图7展示了EMD分解的IMF的显著性检验结果。在显著性检验结果图中,每个能量分布点旁边会标注对应的 IMF 序号。

图7 EMD分解IMF的统计学显著性检验(mitdb-222号记录)
通过显著性检验,我们可以更准确地评估 EMD 分解结果的可靠性和有效性。显著性检验的结果可以帮助我们区分哪些 IMF 是由信号的真实特征引起的,哪些是由噪声引起的。这对于心电信号的特征提取尤为重要,因为心电信号中可能包含多种噪声成分。显著性检验可以帮助我们更准确地提取心电信号的特征,为临床诊断和健康监测提供更有效的工具。
3.2 实验小结
(1)特征提取的有效性:
实验结果表明,HHT 方法能够有效地提取心电信号的特征。通过 EMD 分解,我们可以将复杂的非平稳心电信号分解为多个 IMF,每个 IMF 代表了信号的一个局部特征。通过希尔伯特变换,我们可以计算每个 IMF 的瞬时频率和瞬时幅值,从而实现信号的时频分析。这些特征对于心脏疾病的诊断和监测具有重要意义。
(2)显著性检验结果:
显著性检验的结果表明,某些 IMF 的能量分布超出了 99% 显著性线,这些 IMF 在 99% 的置信水平下是显著的,可以认为它们是由心电信号的真实特征引起的。而其他 IMF 的能量分布未超出显著性线,可以认为它们主要是由噪声引起的。通过显著性检验,我们可以识别并去除那些不显著的 IMF,这些 IMF 主要是由噪声引起的。保留显著的 IMF,可以提高心电信号分析的准确性和可靠性。
Tips:下一讲,我们将进一步探讨,心电信号特征提取——EMD分解、EEMD分解、VMD分解等。
以上就是HHT(希尔伯特黄变换)的全部内容啦~
我们下期再见,拜拜(⭐v⭐) ~
(Ps:有代码实现需求,请见主页信息,谢谢支持!~)
