当前位置：首页 > news >正文

OpenCV-图像分割

news 2025/5/19 7:23:37

实验1

实验内容

上述代码通过使用OpenCV和Matplotlib库来执行以下操作：

读取名为’kt.jpg’的图像文件，并存储在变量img中。
将图像img转换为灰度图像，将其存储在变量gray中。
使用cv2.threshold函数对灰度图gray进行阈值化处理，生成不同类型的二值图像。
a. 使用cv2.THRESH_BINARY类型，将灰度值小于175的像素点设置为0，灰度值大于等于175的像素点设置为255，结果存储在变量thresh1中。
b. 使用cv2.THRESH_BINARY_INV类型，将灰度值小于175的像素点设置为255，灰度值大于等于175的像素点设置为0，结果存储在变量thresh2中。
c. 使用cv2.THRESH_TRUNC类型，将灰度值小于175的像素点保持不变，大于175的像素点设置为175，结果存储在变量thresh3中。
d. 使用cv2.THRESH_TOZERO类型，将灰度值小于175的像素点设置为0，大于等于175的像素点保持不变，结果存储在变量thresh4中。
e. 使用cv2.THRESH_TOZERO_INV类型，将灰度值小于175的像素点保持不变，大于等于175的像素点设置为0，结果存储在变量thresh5中。
创建一个包含标题的列表titles，用于在绘图时显示每个图像的名称。
创建一个包含所有图像的列表images，以便在循环中访问图像数据。
使用循环遍历每个图像，并使用plt.subplot将其显示在一个2行3列的子图中。
设置子图的标题为对应的titles中的名称。
禁用x轴和y轴的刻度。
使用plt.show()显示所有图像。

代码注释

import cv2
import matplotlib.pyplot as pltimg = cv2.imread('kt.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 将灰度图gray中灰度值小于175的点置0，灰度值大于175的点置255
ret, thresh1 = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
# 将灰度图gray中灰度值小于175的点置255，灰度值大于175的点置0
ret, thresh2 = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY_INV)
ret, thresh3 = cv2.threshold(gray, 127, 255, cv2.THRESH_TRUNC)
ret, thresh4 = cv2.threshold(gray, 127, 255, cv2.THRESH_TOZERO)
ret, thresh5 = cv2.threshold(gray, 127, 255, cv2.THRESH_TOZERO_INV)
titles = ['img', 'BINARY', 'BINARY_INV', 'TRUNC', 'TOZERO', 'TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]
for i in range(6):plt.subplot(2, 3, i + 1), plt.imshow(images[i], 'gray')plt.title(titles[i])plt.xticks([]), plt.yticks([])
plt.show()

功能说明

该代码会将原始图像转换为灰度图像，并通过不同类型的阈值化操作生成多幅图像。每幅图像的标题和显示方式都会在绘图中显示。

效果展示

在这里插入图片描述

效果分析比较

通过不同类型的阈值化操作，可以实现对图像的不同程度的二值化处理。具体效果如下：

BINARY：将灰度值小于175的像素点设置为0，大于等于175的像素点设置为255，产生黑白二值图像。
BINARY_INV：将灰度值小于175的像素点设置为255，大于等于175的像素点设置为0，产生反相的黑白二值图像。
TRUNC：将灰度值小于175的像素点保持不变，大于175的像素点设置为175。
TOZERO：将灰度值小于175的像素点设置为0，大于等于175的像素点保持不变。
TOZERO_INV：将灰度值小于175的像素点保持不变，大于等于175的像素点设置为0。

结论

通过不同类型的阈值化操作，可以根据具体需求将图像进行二值化处理，以突出或过滤特定灰度范围的图像特征。这些操作可以在图像处理和分析中起到重要的作用，例如图像分割、轮廓提取等应用场景。

实验2

实验内容

代码使用OpenCV库对图像进行自适应阈值处理。

代码注释

import cv2 as cvsrcImage = cv.imread('kt.jpg')
srcGray = cv.cvtColor(srcImage, cv.COLOR_BGR2GRAY)  # 【2】灰度转换cv.imshow("Src Image", srcImage)
cv.imshow("Gray Image", srcGray)
# 【3】初始化相关变量
# 初始化自适应阈值参数
maxVal = 255
blockSize = 3  # 取值3、5、7....等
constValue = 10
# 自适应阈值算法
adaptiveMethod = 0  # 0:ADAPTIVE_THRESH_MEAN_C，1:ADAPTIVE_THRESH_GAUSSIAN_C
thresholdType = 1  # 阈值类型，0:THRESH_BINARY，1:THRESH_BINARY_INV
# ---------------【4】图像自适应阈值操作-------------------------
dstImage = cv.adaptiveThreshold(srcGray, maxVal, adaptiveMethod, thresholdType, blockSize, constValue);
cv.imshow("Adaptive threshold", dstImage)
cv.waitKey(0)

功能说明

通过cv.imread读取名为’kt.jpg’的图像，将其存储在srcImage中。
使用cv.cvtColor将原始图像转换为灰度图像，存储在srcGray中。
初始化自适应阈值处理的相关参数，包括最大阈值(maxVal)、块大小(blockSize)、常数值(constValue)、自适应方法(adaptiveMethod)和阈值类型(thresholdType)。
使用cv.adaptiveThreshold函数对灰度图像进行自适应阈值处理，将结果存储在dstImage中。

效果展示

Src Image

在这里插入图片描述

Gray Image

在这里插入图片描述

Adaptive threshold

在这里插入图片描述

效果分析比较

自适应阈值处理是根据图像局部区域的灰度情况来确定阈值的一种方法，相比全局阈值，更适应图像局部的变化。
adaptiveMethod为0表示使用均值自适应阈值算法(ADAPTIVE_THRESH_MEAN_C)，为1表示使用高斯自适应阈值算法(ADAPTIVE_THRESH_GAUSSIAN_C)。
thresholdType为0表示二值化类型为THRESH_BINARY，为1表示二值化类型为THRESH_BINARY_INV。
blockSize表示每个块的大小，较小的块大小适用于较小的图像细节，但也可能受到噪声的影响；较大的块大小适用于平滑的图像区域。
constValue是用于调整阈值的常数值。

结论

自适应阈值处理能够有效地处理图像中局部灰度变化较大的情况，通过动态调整阈值，使得不同区域的阈值适应局部特征。在图像处理中，选择合适的自适应阈值方法和参数对于获取清晰的二值图像是很重要的。在这个例子中，通过改变blockSize、constValue、adaptiveMethod和thresholdType等参数，可以观察到不同的效果。

实验3

实验内容

使用OpenCV库对图像进行分割和阈值处理的示例

代码注释

import cv2 as cvsrcImage = cv.imread('kt.jpg')
img = cv.cvtColor(srcImage, cv.COLOR_BGR2GRAY)  # 【2】灰度转换
cv.imshow("Src Image", srcImage);
img = cv.medianBlur(img, 5);  # 中值滤波
ret, dst1 = cv.threshold(img, 127, 255, cv.THRESH_BINARY);  # 固定阈值分割
# 自适应阈值分割，邻域均值
dst2 = cv.adaptiveThreshold(img, 255, cv.ADAPTIVE_THRESH_MEAN_C, cv.THRESH_BINARY, 11, 2);
# 自适应阈值分割，高斯邻域
dst3 = cv.adaptiveThreshold(img, 255, cv.ADAPTIVE_THRESH_GAUSSIAN_C, cv.THRESH_BINARY, 11, 2);cv.imshow("dst1", dst1);
cv.imshow("dst2", dst2);
cv.imshow("dst3", dst3);
cv.imshow("img", img);
cv.waitKey(0);

功能说明

使用cv.imread读取名为’kt.jpg’的图像，将其存储在srcImage中。
使用cv.cvtColor将原始图像转换为灰度图像，将结果存储在img中。
使用cv.medianBlur对灰度图像进行中值滤波，该步骤用于去除图像中的噪声。
使用cv.threshold对滤波后的图像进行固定阈值分割，将结果存储在dst1中。阈值设定为127，大于阈值的像素值设为255，小于等于阈值的像素值设为0。
使用cv.adaptiveThreshold对滤波后的图像进行自适应阈值分割，方法是邻域均值法。将结果存储在dst2中。阈值根据图像的局部区域进行计算，具体阈值计算方式是取邻域中的像素平均值加上一个常数（这里是2）。
使用cv.adaptiveThreshold对滤波后的图像进行自适应阈值分割，方法是高斯邻域法。将结果存储在dst3中。阈值根据图像的局部区域进行计算，具体阈值计算方式是取邻域中的像素加权平均值加上一个常数（这里是2）。

效果展示

Src Image

在这里插入图片描述

dst1

在这里插入图片描述

dst2

在这里插入图片描述

dst3

在这里插入图片描述

img

在这里插入图片描述

效果分析比较

固定阈值分割使用的是固定的全局阈值。根据设定的阈值进行二值分割，可以直接将图像中较亮或较暗的部分分割出来。
自适应阈值分割根据图像局部的特征进行阈值的计算。对于不同的局部区域，根据邻域中的像素值进行调整，适应不同的光照条件和局部变化。
- 邻域均值法：使用邻域中像素的平均值作为阈值。
- 高斯邻域法：使用邻域中像素加权平均值作为阈值，权重由高斯核函数计算得出，离中心像素越近的像素权重越大

结论

不同的阈值分割方法适用于不同的图像和应用场景。固定阈值适用于图像中有明显亮暗差异的分割；而自适应阈值适用于不同光照条件下的图像分割。
中值滤波可以在分割前对图像进行去噪处理，有助于提升分割的准确性。
通过调整阈值、邻域大小和常数等参数，可以对分割结果进行调整，以满足不同的需求和图像特点。

实验4

实验内容

使用OpenCV库对图像进行颜色分离的示例

代码注释

import cv2 as cv
import numpy as npdef color_seperate(image):hsv = cv.cvtColor(image, cv.COLOR_BGR2HSV)  # 对目标图像进行色彩空间转换lower_hsv = np.array([100, 43, 46])  # 设定蓝色下限upper_hsv = np.array([124, 255, 255])  # 设定蓝色上限# 依据设定的上下限对目标图像进行二值化转换mask = cv.inRange(hsv, lowerb=lower_hsv, upperb=upper_hsv)# 将二值化图像与原图进行“与”操作；实际是提取前两个frame 的“与”结果，然后输出mask 为1的部分dst = cv.bitwise_and(src, src, mask=mask)  # 注意：括号中要写mask=xxxcv.imshow('result', dst)  # 输出src = cv.imread('test.jpg')  # 导入目标图像，获取图像信息
color_seperate(src)
cv.imshow('image', src)
cv.waitKey(0)
cv.destroyAllWindows()

功能说明

使用cv.cvtColor将原始图像从BGR色彩空间转换为HSV色彩空间，将结果保存在hsv中。
设定颜色的下限lower_hsv和上限upper_hsv，表示在该颜色范围内的像素会被保留，其他颜色的像素则被过滤。
使用cv.inRange根据设定的上下限对图像进行二值化，将落在颜色范围内的像素设置为白色（255），其他像素设置为黑色（0），结果保存在mask中。
使用cv.bitwise_and将二值化图像与原始图像进行按位与操作，提取颜色范围内的部分，结果保存在dst中。
使用cv.imshow展示结果图像dst和原始图像src。
使用cv.waitKey等待用户按下键盘按键。
使用cv.destroyAllWindows关闭所有图像窗口。

效果展示

result

在这里插入图片描述

效果分析比较

根据设定的颜色下限和上限，将图像中在颜色范围内的部分保留下来，其他部分被过滤掉。这样做可以聚焦于感兴趣的颜色区域，突出图像中特定颜色的部分。

结论

颜色分离可以用于目标检测、图像分割等应用场景。通过设定不同的颜色下限和上限，可以实现对不同颜色的分离。需要根据具体的实际需求，调整颜色范围的设定，以满足对特定颜色的提取要求。

基于阈值化的分割方法

实验内容

基于阈值化的分割方法

此方法实质是利用图像的灰度直方图信息得到用于分割的阈值

Ostu 法，最频值法( Mode 法)，·矩量保持法

用以上三种阈值分割方法的实现算法，代码实现并进行结果对比##

代码

import cv2 as cv
import numpy as np# Otsu 法 - 通过自动确定阈值进行图像分割
def otsu_threshold(image):# 转换图像为灰度gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)# 使用 Otsu 方法获取阈值和分割结果_, otsu_result = cv.threshold(gray, 0, 255, cv.THRESH_BINARY + cv.THRESH_OTSU)return otsu_result# 最频值法 (Mode 法) - 使用灰度直方图中的众数作为阈值
def mode_threshold(image):# 转换图像为灰度gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)# 计算灰度直方图hist = cv.calcHist([gray], [0], None, [256], [0, 256])# 找到直方图中的众数（Mode）mode = np.argmax(hist)# 使用众数作为阈值进行分割_, mode_result = cv.threshold(gray, mode, 255, cv.THRESH_BINARY)return mode_result# 矩量保持法 - 通过保持灰度矩量的方法确定阈值
def moment_preserving_threshold(image):# 转换图像为灰度gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)# 计算灰度直方图hist = cv.calcHist([gray], [0], None, [256], [0, 256])# 计算灰度矩量total_pixels = sum(hist)sum_moments = [(idx + 1) * hist[idx] for idx in range(len(hist))]sum_moments = np.sum(sum_moments)# 计算阈值threshold = int(sum_moments / total_pixels)# 使用阈值进行分割_, moment_preserving_result = cv.threshold(gray, threshold, 255, cv.THRESH_BINARY)return moment_preserving_result# 读取图像
src = cv.imread('test.jpg')# 调用各个阈值分割方法
otsu_result = otsu_threshold(src)
mode_result = mode_threshold(src)
moment_preserving_result = moment_preserving_threshold(src)# 显示原始图像和分割结果
cv.imshow('Original Image', src)
cv.imshow('Otsu Result', otsu_result)
cv.imshow('Mode Result', mode_result)
cv.imshow('Moment Preserving Result', moment_preserving_result)# 等待按键
cv.waitKey(0)
cv.destroyAllWindows()

效果展示

在这里插入图片描述

效果比较分析

Otsu方法、最频值法和矩量保持法是图像分割中常用的三种方法，它们各自有不同的原理和适用场景。下面是对它们的简要比较：

Otsu方法：
- 原理： Otsu方法基于图像的灰度直方图，通过最大类间方差的方法自动确定一个灰度阈值，将图像分成两个类别（前景和背景）。
- 优点： 对于具有双峰直方图的图像效果好，自动选择阈值，无需人工干预。
- 缺点： 在直方图单峰的情况下可能不太准确。
最频值法：
- 原理： 最频值法通过寻找灰度直方图中的峰值，选择峰值对应的灰度值作为分割阈值。
- 优点： 简单直观，对于单峰直方图的图像效果较好。
- 缺点： 对于复杂场景的图像可能不够灵活，适用性有限。
矩量保持法：
- 原理： 矩量保持法利用图像的矩特性，通过最小化目标函数实现分割，以保持目标区域的矩特性。
- 优点： 对于复杂场景和具有多个区域的图像效果较好，能够保持目标的形状特性。
- 缺点： 计算相对较复杂，需要对图像的矩进行处理。

结论

综合来看，选择哪种方法取决于图像的特性以及具体的分割需求。如果图像具有明显的双峰直方图，Otsu方法可能更合适；如果图像简单且直方图单峰，最频值法可能更适用；而对于需要保持目标形状特性的场景，矩量保持法可能是一个更好的选择。通常，在实际应用中，需要根据具体情况进行实验和调整，选择最适合的分割方法。

指令

基于聚类的分割方法

K-Means算法

代码实现

import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# 计算欧拉距离
def calcDis(dataSet, centroids, k):clalist = []for data in dataSet:diff = np.tile(data, (k,1)) - centroids  # 相减   (np.tile(a,(2,1))就是把a先沿x轴复制1倍，即没有复制，仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))squaredDiff = diff ** 2  # 平方squaredDist = np.sum(squaredDiff, axis=1)  # 和  (axis=1表示行)distance = squaredDist ** 0.5  # 开根号clalist.append(distance)clalist = np.array(clalist)  # 返回一个每个点到质点的距离len(dateSet)*k的数组return clalist# 计算质心
def classify(dataSet, centroids, k):# 计算样本到质心的距离clalist = calcDis(dataSet, centroids, k)# 分组并计算新的质心minDistIndices = np.argmin(clalist, axis=1)  # axis=1 表示求出每行的最小值的下标newCentroids = pd.DataFrame(dataSet).groupby(minDistIndices).mean()  # DataFramte(dataSet)对DataSet分组，groupby(min)按照min进行统计分类，mean()对分类结果求均值newCentroids = newCentroids.values# 计算变化量changed = newCentroids - centroidsreturn changed, newCentroids# 使用k-means分类
def kmeans(dataSet, k):# 随机取质心centroids = random.sample(dataSet, k)# 更新质心 直到变化量全为0changed, newCentroids = classify(dataSet, centroids, k)while np.any(changed != 0):changed, newCentroids = classify(dataSet, newCentroids, k)centroids = sorted(newCentroids.tolist())  # tolist()将矩阵转换成列表 sorted()排序# 根据质心计算每个集群cluster = []clalist = calcDis(dataSet, centroids, k)  # 调用欧拉距离minDistIndices = np.argmin(clalist, axis=1)for i in range(k):cluster.append([])for i, j in enumerate(minDistIndices):  # enymerate()可同时遍历索引和遍历元素cluster[j].append(dataSet[i])return centroids, cluster# 创建数据集
def createDataSet():return [[1, 1], [1, 2], [2, 1], [2, 3], [6, 4], [6, 3], [5, 4], [5, 2]]if __name__ == '__main__':dataset = createDataSet()centroids, cluster = kmeans(dataset, 2)print('质心为：%s' % centroids)print('集群为：%s' % cluster)for i in range(len(dataset)):plt.scatter(dataset[i][0], dataset[i][1], marker='o', color='green', s=40, label='原始点')#  记号形状       颜色      点的大小      设置标签for j in range(len(centroids)):plt.scatter(centroids[j][0], centroids[j][1], marker='x', color='red', s=50, label='质心')plt.show()

功能说明

功能说明：

calcDis函数计算样本点到质心的欧拉距离；
classify函数根据欧拉距离进行分类，并计算新的质心；
kmeans函数使用K-means算法对数据集进行聚类，随机选择质心并迭代更新质心，直到变化量全为0；
createDataSet函数创建一个样本数据集。

效果展示

数据集为[[1, 1], [1, 2], [2, 1], [2, 3], [6, 4], [6, 3], [5, 4], [5, 2]]时

在这里插入图片描述

数据集为[[1, 1], [1, 2], [2, 1], [2, 2], [6, 4], [6, 3], [5, 4], [5, 3]]时

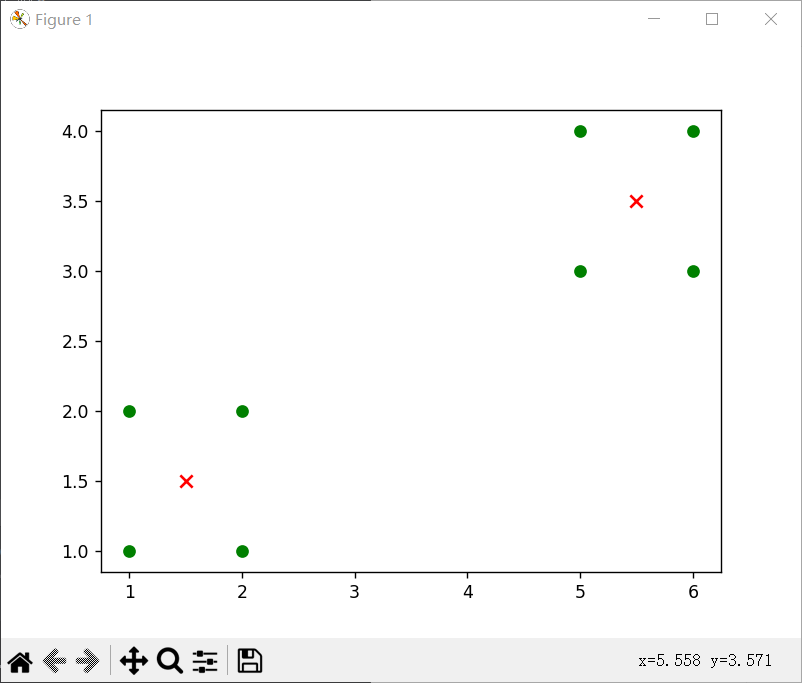
在这里插入图片描述

k=3时，数据集为[[1, 1], [1, 2], [2, 1], [2, 2], [6, 4], [6, 3], [5, 4], [5, 3]]时

(1)

在这里插入图片描述

(2)

在这里插入图片描述

效果对比分析

可以发现，k相同时，数据集决定对应质点的位置，从中我们可以看出当数据不一样时，质点会出现在不同的位置，但是总是会在对应某几个数据集（或者1个）的点的中心。

当k=3时候，出现三个质点，但是由于随机的关系，两次效果不同，(1)是单独一个点，四个点，和三个点这样分，而(2)就是2、2、4这样分的对应质点。

结论

根据代码的输出和可视化结果，可以得出以下结论：

经过K-means聚类算法处理后，数据集被划分为2个簇，每个簇由多个样本组成；
质心坐标表示了每个簇的中心位置；
可视化结果展示了原始点和质心的分布情况。

需要注意的是，对于不同的数据集和初始质心以及k值的选择的选择，K-means算法的结果可能会有所不同。因此，在实际应用中，可能需要多次运行算法并选择最优结果。

Mean-Shift算法

代码

import numpy as np  # 导入NumPy库用于数学计算
from sklearn.datasets import make_blobs  # 导入make_blobs函数用于生成数据集
import matplotlib.pyplot as plt  # 导入Matplotlib库用于可视化# 定义欧氏距离计算函数
def euclidean_distance(x1, x2):return np.sqrt(np.sum((x1 - x2) ** 2))# 定义高斯核函数
def gaussian_kernel(distance, bandwidth):return (1 / (bandwidth * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((distance / bandwidth) ** 2))# 定义Mean Shift算法函数
def mean_shift(data, bandwidth=2):centroids = data.copy()  # 初始化聚类中心为数据点本身for i in range(len(data)):  # 遍历每个数据点x = centroids[i]  # 当前数据点while True:distances = [euclidean_distance(x, xi) for xi in centroids]  # 计算当前点与所有点的距离weights = [gaussian_kernel(d, bandwidth) for d in distances]  # 计算每个点的权重prev_x = x  # 保存上一次的点x = np.dot(weights, centroids) / np.sum(weights)  # 更新当前点的位置为加权平均# 检查是否收敛，如果当前点与上一次点的距离小于阈值，则认为收敛if euclidean_distance(x, prev_x) < 1e-5:breakcentroids[i] = x  # 将当前点设为收敛后的点# 合并重复的聚类中心，如果两个聚类中心距离小于阈值，则认为是同一个中心unique_centroids = [centroids[0]]for i in range(1, len(centroids)):is_unique = Truefor j in range(len(unique_centroids)):if euclidean_distance(centroids[i], unique_centroids[j]) < 1e-5:is_unique = Falsebreakif is_unique:unique_centroids.append(centroids[i])return np.array(unique_centroids)  # 返回最终的聚类中心# 生成数据集，这里使用make_blobs生成一个带有四个簇的数据集
data, _ = make_blobs(n_samples=300, centers=4, cluster_std=1.0, random_state=42)# 使用Mean Shift算法进行聚类，指定带宽参数为2
centroids = mean_shift(data, bandwidth=2)# 可视化结果
plt.scatter(data[:, 0], data[:, 1], s=30, color='blue', label='Data points')  # 绘制原始数据点
plt.scatter(centroids[:, 0], centroids[:, 1], s=100, color='red', marker='X', label='Cluster Centers')  # 绘制聚类中心点
plt.title('Mean-shift Clustering')  # 设置标题
plt.legend()  # 显示图例
plt.show()  # 显示图形

功能说明

功能说明：

euclidean_distance函数计算两个点之间的欧氏距离；
gaussian_kernel函数定义了高斯核函数，用于计算每个点的权重；
mean_shift函数实现了Mean Shift算法，通过迭代更新每个点的位置，直到收敛为止；
make_blobs函数生成了一个带有四个簇的数据集；
最后，代码将原始的数据点和聚类中心点在二维坐标中以不同颜色进行了绘制。

效果展示

在这里插入图片描述

结论

基于生成的数据集和指定的带宽参数，Mean Shift算法对数据进行了聚类，并成功找到了聚类中心点。通过可视化结果可以清楚地看到每个簇的中心位置和数据点的分布情况。需要注意的是，聚类结果可能会受到带宽参数的影响，不同的参数可能会得到不同的聚类结果。在实际应用中，可以通过尝试不同的参数值来优化聚类效果。

查看全文

http://www.xdnf.cn/news/516349.html