当前位置：首页 > news >正文

疲劳分析后处理参数意义？

news 2025/5/17 11:56:32

1、疲劳分析是工程力学和材料科学中的一项重要研究内容，主要用于评估材料或结构在反复载荷（循环应力或应变）作用下逐渐产生损伤、裂纹萌生及扩展，并最终导致失效的过程。这种失效称为疲劳失效，其特点是破坏时的应力可能远低于材料的静态强度极限。

SN曲线

2、疲劳分析结果分类

（1）Life（疲劳寿命）

定义：

材料或结构在特定循环载荷下发生失效前的循环次数（Nf），通常基于S-N曲线（应力-寿命法）或应变-寿命法（ε-N曲线）计算。

计算方法：

高周疲劳（应力控制）：通过S-N曲线（如Basquin公式）预测寿命

σa(交变应力幅):

应力循环中的交变部分(最大值与最小值之差的一半)，单位为 MPa。

σ'f(疲劳强度系数):

材料的固有属性，表示单轴疲劳试验中应力幅与疲劳寿命关系的基准值，单位为 MPa。

Nf(疲劳寿命):

材料在交变应力作用下发生失效的循环次数(无单位)。

b(Basquin 指数):

负值常数，描述应力幅与疲劳寿命的幂律关系(无单位)。

低周疲劳（应变控制）：通过Manson-Coffin公式预测寿命

Δε（总应变范围）：每个循环中的总应变变化量(弹性应变 +塑性应变)，无单位。

E(弹性模量)：材料的刚度指标，单位为 MPa。

ε'f(疲劳延性系数):材料的固有属性，表示塑性应变幅与疲劳寿命关系的基准值，无单位。

C(Coffin-Manson 指数):负值常数，描述塑性应变幅与疲劳寿命的幂律关系(无单位)

作用：直接反映结构的耐久性，用于优化设计或制定维护计划。

（2）Damage（累积损伤）

定义：
根据Miner线性累积损伤理论，损伤值（D）表示各应力幅值对材料造成的疲劳损伤之和，当 D=1 时预测失效。公式：

ni：第i个应力水平的实际循环次数。

Nf,i:第i个应力水平对应的疲劳寿命。

作用：量化多级载荷或变幅载荷下的累积损伤，用于寿命预测。

（3）SafetyFactor（安全系数）

定义：
实际应力或寿命与许用值的比值，反映设计的安全裕度。

常见类型：

应力安全系数：SFσ=许用应力/实际应力

寿命安全系数：SFN=预测寿命/设计寿命

作用：避免因载荷波动、材料分散性或模型误差导致的意外失效。

（4）BiaxialityIndication（双轴性指标）

定义：
量化多轴应力状态下主应力的比例关系，常用参数包括：

双轴应力比λ=σ1/σ2，其中σ1>σ2

相位角Θ（主应力方向随时间的变化）。

作用：
判断疲劳失效模式（如裂纹方向）并修正等效交变应力。

（5）EquivalentAlternatingStress（等效交变应力）

定义：
将多轴应力状态转换为等效的单轴交变应力（σa,eq），以便使用单轴S-N曲线进行寿命预测。

常用准则：

VonMises准则（适用于延性材料）：

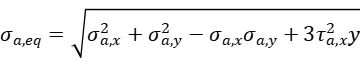
σa,x: (x方向交变正应力)：

x方向上的周期性交变正应力幅值，表征该方向动态载荷的强度。

σa,y(y方向交变正应力):

y方向上的周期性交变正应力幅值，反映该方向动态载荷的强度。

Ta,xy(xy平面交变剪切应力):

xy平面内的交变剪切应力幅值，描述剪切载荷的动态变化特性，

-σa,x+σa,y：

正应力分量的相互作用项，负号表示x和y方向正应力的部分抵消效应。

剪切应力项的等效贡献，系数3由Von-Mises准则推导得出，用于将剪切应力转换为等效正应力。

最大主应力准则（适用于脆性材料）：

结合平均应力修正（如Goodman、Gerber）：

作用：
简化多轴疲劳分析，兼容单轴疲劳数据。

（6）参数间的相互关系

参数	输入/输出关系	工程意义
等效交变应力→寿命	越大，越小（S-N曲线规律）	直接决定寿命预测结果
双轴性指标→等效应力	双轴性影响的计算（如VonMises修正）	多轴载荷需通过等效应力映射到单轴模型
寿命→损伤	单个循环损伤为，总损伤	损伤累积用于评估变幅载荷下的剩余寿命
安全系数→设计优化	SF<1表示危险，需降低应力或增加材料强度，SF>1表示安全	指导设计修改以满足可靠性要求

3、疲劳分析修正理论

在疲劳分析中，Goodman、Soderberg、Gerber、ASMEElliptical 等理论是用于修正非零平均应力（MeanStress）对疲劳寿命影响的经典模型。这些模型通过将实际载荷等效为对称循环载荷（R=−1），从而利用对称循环下的疲劳数据（S-N曲线）进行寿命预测。以下是这些理论的核心公式、曲线特征及适用场景的详细对比：

（1）Goodman理论（GoodmanLine）

公式：

假设：
平均应力 σm与交变应力幅 σa呈线性关系，忽略材料的塑性变形能力。

曲线形状：
在σm-σa
坐标系中为一条直线，连接点 (σuts,0)和 (0,σfatigue)。

适用场景：

脆性材料（如铸铁、陶瓷）。

高周疲劳（低应力幅、高循环次数）。

保守设计（预测寿命偏短，安全系数高）。

缺点：
对于延性材料（如钢、铝合金），可能过于保守，低估实际疲劳强度。

（2）Soderberg理论

公式：

假设：
用屈服强度
代替Goodman公式中的极限抗拉强度σuts ，确保材料不进入塑性变形。

曲线形状：
与Goodman线类似，但终点为 (σy,0)，曲线更陡峭（因 σy<σuts）。

适用场景：

低周疲劳（高应力幅，可能发生局部屈服）。

需避免塑性变形的场合（如精密机械部件）。

极度保守设计（比Goodman更严格）。

缺点：
过度保守，可能导致材料利用率不足。

（3）Gerber理论（GerberParabola）

公式：

假设：
平均应力与交变应力呈抛物线关系，考虑材料的延展性。

曲线形状：
在σm-σa 坐标系中为一条开口向下的抛物线，位于Goodman线上方。

适用场景：

延性材料（如钢、铝合金）。

中高周疲劳（更贴近实验数据）。

缺点：
在 σm接近σuts时可能过于乐观。

（4）ASME Elliptical（ASME椭圆准则）

公式：

假设：
结合Goodman和Gerber的特点，形成椭圆轨迹，平衡保守性与实际数据。

曲线形状：
在σm-σa坐标系中为四分之一椭圆，连接点(σuts,0)和 (0,σfatigue) 。

适用场景：

ASME锅炉与压力容器规范推荐的标准方法。

多轴疲劳分析（需结合等效应力准则）。

需平衡安全性与经济性的设计。

特点：
介于Goodman和Gerber之间，适用于通用工程材料。

（5）平均应力修正曲线对比

理论	公式	曲线形状	使用材料	保守性	典型标准
Goodman		直线	脆性材料	高	通用设计
Soderberg		陡峭直线	需避免塑性的场合	极高	低周疲劳
Gerber		抛物线	延性材料（钢、铝等）	低	中高周疲劳
ASME Elliptical		椭圆	通用工程材料	中等	ASME BPVC