当前位置：首页 > news >正文

考研408《计算机组成原理》复习笔记，第三章数值数据的表示和运算（定点数篇）

news 2025/5/11 5:48:23

这一章主要就是计算、单位换算，所以废话不多说，直接重点概念和讲计算技巧即可。（这里默认大家已经基本大概知道二进制、八进制、十六进制、浮点数....这些最基础的东西了）

；

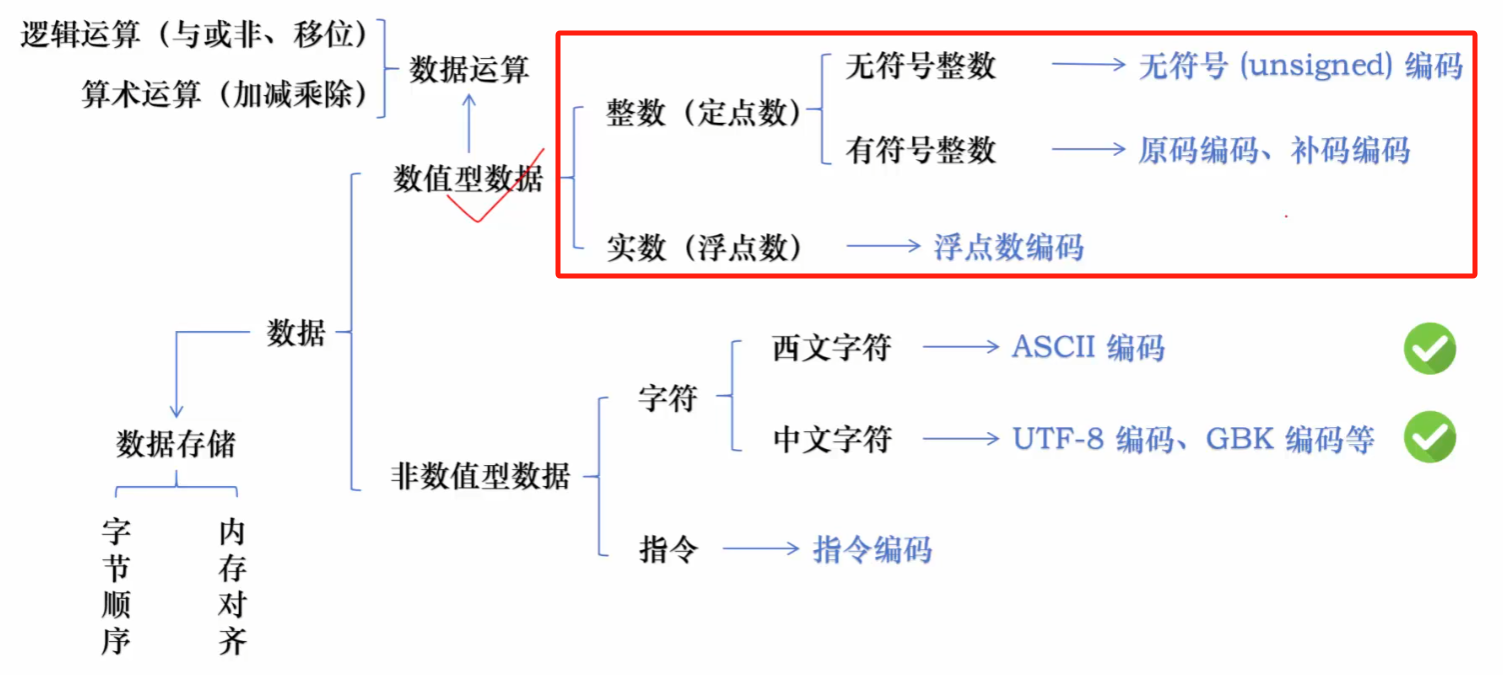
另外，这一章讲的是数值型的数据的表示和运算，数据除了数值型，还有非数值型

一、一些基本概念

1、机器的数值分类

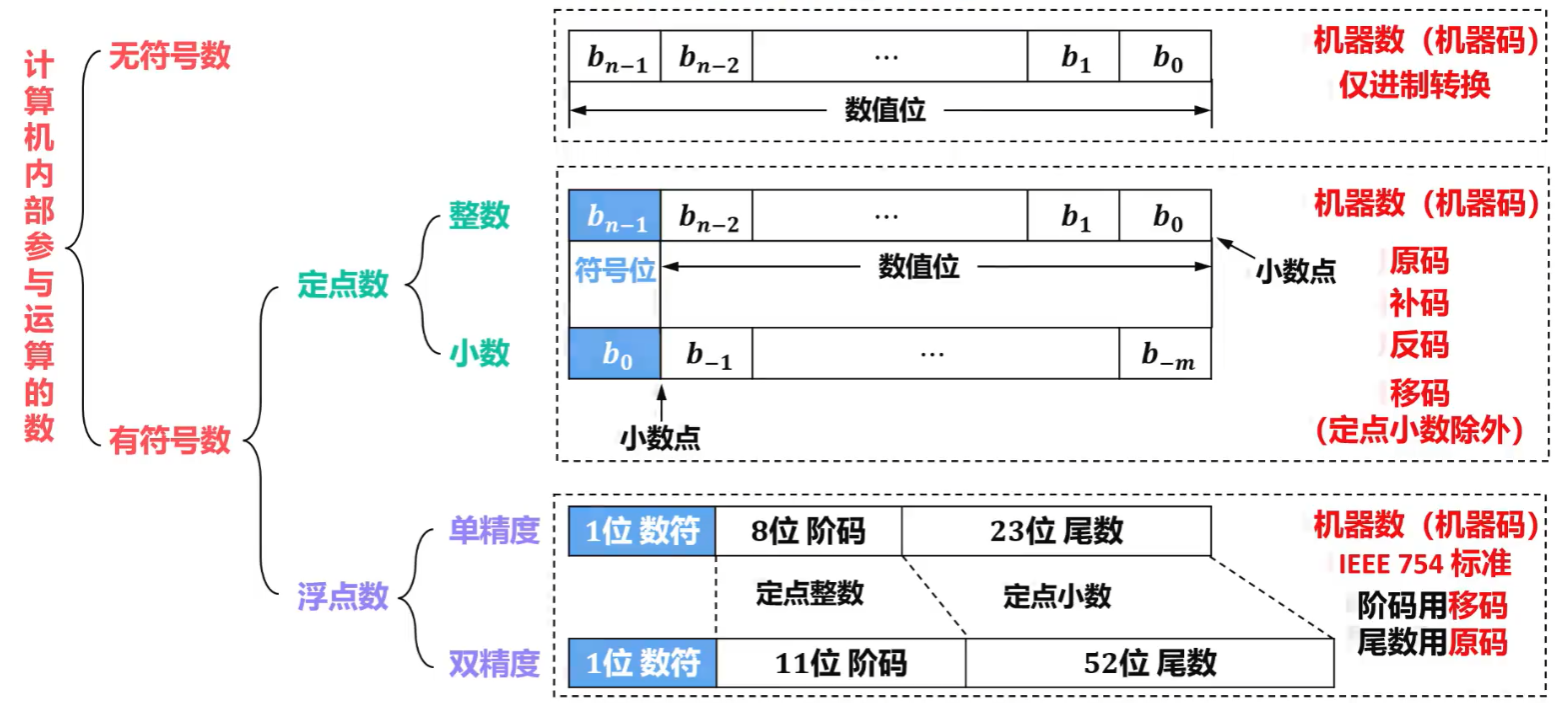
数值型数据主要分为【无符号数】和【有符号数】

【无符号数】就是没有正负号（即是正数，像计算机里的内存地址、数组下标，无需考虑负数情况）
【有符号数】就是有正负号，又分为【定点数】和【浮点数】
【定点数】就是小数点固定的数，也分为【整数】和【纯小数】
【整数】：小数点固定在最右边（数学里整数一般忽略最右边小数点，但是计算机里要考虑）
【纯小数】：小数点在最左边（0.xxx这样，理解为整数部分是0）

【浮点数】：也叫“带小数”，小数点不固定（xxx.xxx这样，我们可以理解为整数部分不为0的带小数），还分为【单精度】和【双精度】
【单精度】
【双精度】

那么为什么机器里的二进制数值是这几种呢？他们又是如何在机器里表示的？难道+、-、.、这些符号可以在机器里表示出来吗？

对应的就是机器数里的【机器码】了

2、机器的数值的各种进制

各个进制的专业表示方法：

如果英文单词记不住就这样：“十D、二B、八O、十六H”——>“师弟，2B，欧巴，石榴红”

；

然后对应C语言的标识符就：十就是数所以没有前缀，其他进制都有前缀而且都带有0，二进制是B就0b、八进制是O两个圆圈不好看就一个0、十六进制就16岁小孩太小了，不让玩推特x.......（当然你有更好的记忆方法可以不按我的）

二、开始计算

1、总的互相换算的技巧

2、2进制、8进制、16进制 —> 10进制

二进制的幂次方表，记熟了以后方便快速换算

三个进制转换成10进制的规则

1）N进制就是每一位的【这一位数值 * N^位】相加之和，搞定

（小数部分的次方是负数、整数右边第一位是【第0位】，小数左边第一位是【第-1位】）

2）也可以把8进制、16进制都换成2进制来转换

二进制还有一个技巧是我个人总结的，就是当这几位都是1111....没有0的时候，十进制就是【2^(最高位+1) - 1】，比如【1111】就是【2^4 - 1 = 16 -1 = 15】；

那么同理，如果中间有0的情况，你就先根据最高位【2^(最高位+1) - 1】来假设全都是1，然后再减去有0的位数不就行了，比如【11110000】就是【(2^8 - 1) - (2^4 - 1) = 255 - 15 = 240】

当然像这种中间1和0断开得这么乱的就没办法用我的方法了，你还是老老实实按原来的规则全都展开，我的方法只适用于1或0连续挨着的情况

3、2进制—>8进制、2进制—>16进制

因为8进制就是0-8嘛，16进制0-16

那二进制就1和0两个数，通过排列组合我们可以发现2^3=8，也就是三位的二进制刚好有8种排列组合可以对应8个数；2^4=16，也就是四位的二进制刚好有4种排列组合可以对应16个数

刚好复习计算机网络的通信原理，学过的可以回想一下，8种状态的码元是不是对应 $log_{2}^{8}$ = $log_{2}^{2^{3}}$ = 3bit，16种状态码元对应 $log_{2}^{16}$ = $log_{2}^{2^{4}}$ = 4bit。没学过的跳过，当我没说。

所以：

2进制转换8进制时，3位一组，前后不够3位的补0；

2进制转16进制时，4位一组，前后不够4位的补0。

然后每一组按照2进制转10进制规则即可得出每一位的值，合起来就行了

（技巧就是，三位的时候牢记每一组是421、四位的时候牢记每一组是8421）

换回二进制则是反着来即可

每一位的数都先组成2进制（八进制就配421、十六进制配8421）

然后再用二进制变回去

4、8进制—>16进制

以2进制为桥梁，先转成2进制，再转成8或16进制即可

5、10进制转任意制

记住两个公式【除基取余】和【乘基取整】

【除基取余】是针对整数部分

一直对被除数除【进制数】，除到被除数成为0为止，所有的余数【从下到上】代表二进制【从左到右】

【乘基取整】是针对小数部分

一直对小数结果乘【进制数】，乘到小数结果的小数部分为0为止，所有结果的整数部分【从上到下】代表小数部分的【从左到右】

结合起来

；

提示：当出现无限循环小数的时候是在所难免的，这种情况达到题目要求的精度即可

；

另外，记住：并非所有10进制都可以用2进制表示

例题：

总结

把下面表背熟背烂

；

拓展：二进制幂次方的表记熟了还有利于计算机网络的IP地址子网掩码的计算（学过计算机网络的可以简单看看）

例题（出现的很少，每一年基本只可能出一道，但是这种纯加减乘除的送分题不能不要）

三、（重点）机器码

首先，在讲一下【真值】和【机器数】的概念

真值就是我们正常生活表达的数值：+2、-193....
机器数就是把正负号、数值全都用二进制1/0来表示，后面会讲

通常机器数都是1个字节(8位)的二进制来表示，当出现溢出最小或最大可表示范围的时候才可能用2个字节(16位)或更多位。

1、无符号数的编码

首先，无符号数我们可以知道，是没有【符号位】的，而且也【不表示小数】，所以对应二进制编码是多少位——>对应的数值就是是多少

那么无符号整数的范围，就如我前面二进制转换十进制的技巧，最小值是全是0，最大值是全是1，而全是1的十进制结果就是【2^n-1】；所以无符号数表示范围是【0~2^n-1】

另外，无符号数不能直接运算，因为一旦【溢出】，结果就会错误

这里计算技巧是：逢二进位一，当进位超出最大表示范围就会溢出，溢出就会直接舍掉溢出的最高位，导致结果错误

例题：

2、有符号数编码

1）原码

对于有符号数的第1种表示就是：原码

他为了表示正负号就在最高位在加了1位

——原码表示规则

正数符号位是0、负数符号位是1；其他位正常按十进制换成的二进制形式表示就行，就这么简单

——原码符号位表示真值0的方式、缺点

因为原码表示的+0、-0会有两种不同的表达形式，但实际的真值的-0=+0；而且原码的首位是符号位，参与运算会导致结果出错，所以计算机里并不是把原码直接作为运算的形式

——原码的可表示范围：

对于【原码】的n位编码可表示的范围是如下图：

和无符号数范围的区别就在于——>

1、有符号数是有负数的，最小值是包括符号位全是1，最大值是符号位是0后面都是1

2、定点数有正负符号，所以最高位不能算数值，可表示的数值要算【n-1】位

——原码在计算机的用处

补充重点：原码因为【不利于减法】和【有两种0表示法】的缺点，无法直接用于计算，它真正的意义只是表示【浮点数的尾码】（后面会学）

2）反码

为了解决【原码不利于减法运算】的问题，人们又想到了发明【补码】，但在学习补码之前，我们先学习【反码】，因为【反码】的意义就是作为【原码】—>【补码】的 “中间过渡码”，仅此而已

——反码表示规则

使用转换规则也很简单：

正数：【反码】=【原码】=【补码】，三者一样

负数：【反码】=【原码】符号位不变，数值位全取反

——反码的表示真值0的方式

另外，反码和原码的符号位一样，所以对于真值0也有两种表示方法

不过区别在于【原码-0】是【首位1、后面全0】，【反码-0】是【首位1，后面全取反为1】

——反码的可表示范围

——反码在计算机的用处

补充重点：然后【反码】连加法运算都不方面，更不可能适合运算了，目前计算机不用它计算，他的意义仅仅就是作为【原码】—>【补码】的 “中间过渡码”

3）补码

既然【原码】、【反码】都不能用于计算，那只能靠【补码】了

【补码】的意义就是用【补数之间的加法】等价替换【真值之间的减法】

这样就从【被减数 - 减数 = 结果】变成【被减数的补数 + 减数补数 = 结果的补数】

——补码表示规则

使用转换规则也很简单：

正数：【补码】=【原码】=【反码】，三者一样

负数：【补码】=【反码】最后一位+1 =【原码】符号位不变，后面全取反，最后一位+1

——补码转换真值、原码的重要技巧！！！

重要技巧！！！！！

(1)【补码】转【原码】，不需要先减1再数值位取反！！！

大家知道【原码】怎么转换【补码】之后，肯定觉得【补码】变回【原码】就是按原路返回，先减1再把数值位取反，但是不用！！！！减法永远都是最麻烦的！！！

记住了：【补码】<——>【原码】都是符号位不变，数值位取反后加1

例子：

；

；

(2)【补码】转【真值】，不需要先转制成原码！！！

补码的符号位可以直接参与计算，规则是：

【符号位】是1，首位就是负数；【符号位】是0，首位就是正数。
【符号位】和其他位都直接按二进制转十进制规则，相加即可
但是别忘了，正数情况不用，正数的补码就是原码

例子：

该例子首位符号位是1，而且是第6位，则第一位是-2^6，其他位正常分别是2^5、2^3，所以结果就是【-2^6 + 2^5 + 2^3 = -24】

；

(3)【X补码】转【-X转码】

就是【X补码】连同符号位一起取反，然后末尾加1

自己试一下就知道了，比如X=+1001，补码=0,1001；-X=-1001，补码=1,0111

——补码的表示真值0的方式

——补码可表示的范围

；

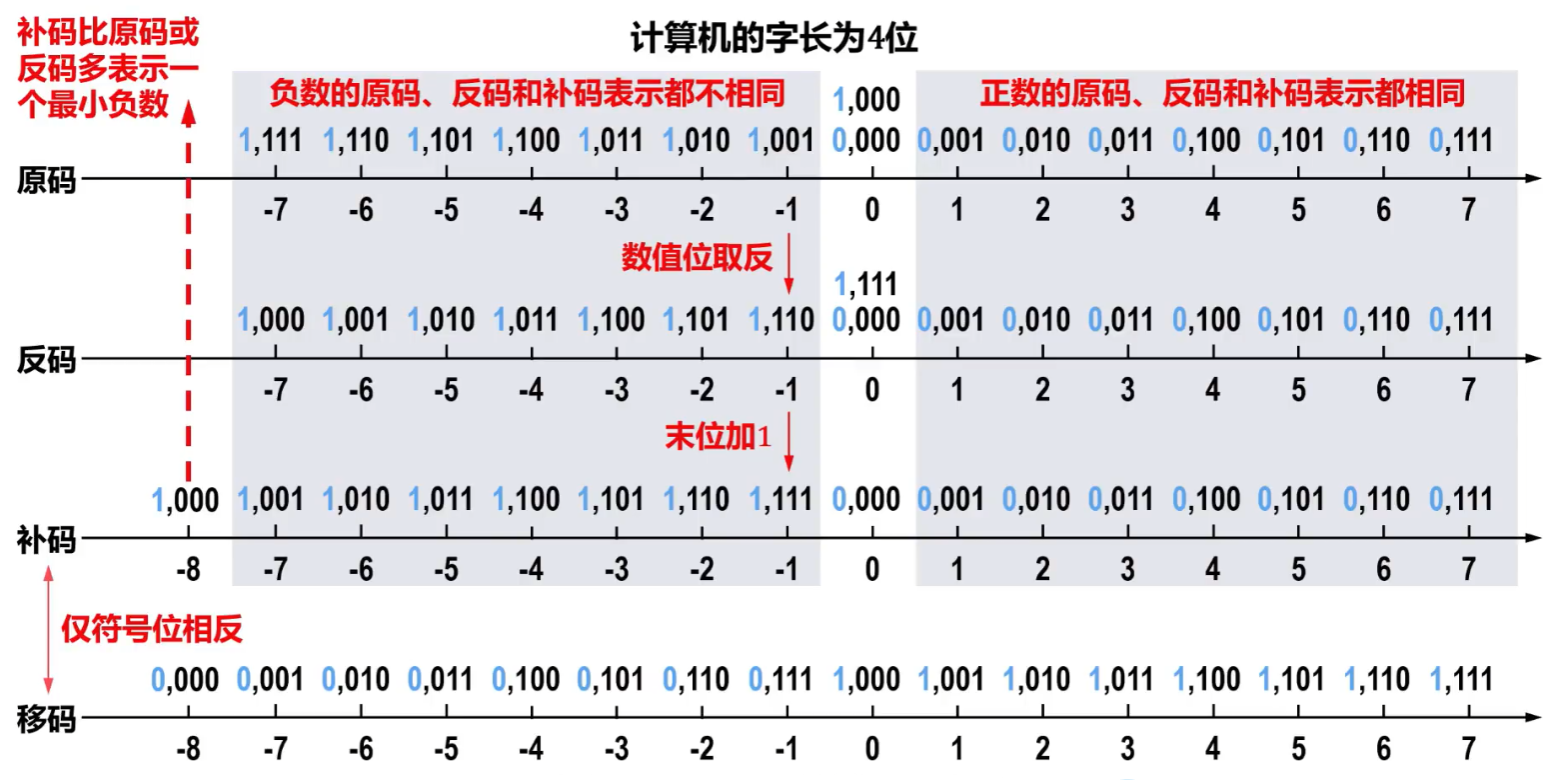
记住：反正就是最小值范围比【原码】和【反码】多1个

多这个的原因是【原码】和【反码】都用了两个二进制数来一个真值0

【补码】只用一个二进制数000...000来表示一个真值0
而且【补码】的 “ 首位符号位 ” 既可以表示符号、也可以表示数值参与计算
然后 100...0(N+1位) 就是比 11...1(N位) 多1，自己算一下就知道了

那同样是8位、16位...，多余的1000...00这个二进制就可以多表示一个最小值！！！

——补码在计算机的作用

只有【补码】可以在计算机用来计算！！！！

留意：

所以换个说法说：【有符号数(主要指定点整数)】都是【补码】表示！！（这句话背熟！！）

——补码原理（不感兴趣可以不看，不重要）

【十进制抽象概念理解】

类似钟表一样，对于负数，可以用【其表示范围最大值】-【该负数】=【补数正数】，其中这个【补数正数】来等价这个【负数】

【加减法正式运算概念代入理解】

挑重点：

1、N位的十进制的【补数】是【999...9 - 该数 + 1】，N位的二进制的【补数】是【111...1 - 该数 + 1】
2、十进制的减法用补数表示是【被减数的补数 + 减数的补数 = 结果的补数】，二进制的减法用补数表示同样也是【被减数的补数 + 减数的补数 = 结果的补数】
3、结合上面两个概念，十进制里的(999...9 + 1)就是【模】，二进制里的(111...1 + 1)也是【模】，本质上就是用十进制或二进制的的1000...0这个【模】来求补数，之所以拆要拆开是因为要考虑到【减法借位】的问题，所以拆成十进制里的(999...9 + 1)、二进制里的(111...1+1)

——补码例题

4）原码、反码、补码的整体计算流程

这里引用一个我觉得总结的很好的一个b站评论：

具体例子：

总结

5）移码

——移码表示规则

1、真值＋2^N(N是真值的位数，不包括机器码的符号位，相对机器码是N-1)
2、补码的符号位取反即可

——移码表示真值0的形式

和补码一样只有一种表示形式

注意：

——移码表示的范围

也和补码一样

——移码的原理（也可以不看）

——移码在计算机的作用

就是用来比较真值大小、还有作为浮点数的阶码（后面会讲）

6）总结四码

【搭配定点小数】

本质差不多，

——例题

四、数据扩展：零扩展、符号扩展

1、概念

各个类型的数据有指定的位数范围，而ALU、通用寄存器也有不同的固定的位数，当各个数据存放到ALU和通用寄存器时，就要把多余的空位补齐，这就叫数据扩展

当然还有像C语言里【short短整型】转变成【int整型】或【long长整型】也都要扩展

2、零扩展和符号扩展

那到底怎么扩展呢？规则如下

无符号数用零扩展：多出来的位用【0】补满

有符号数用符号扩展：多出来的数用【符号位】补满（原理是计算机里的数是补码，补码负数扩展位都是1，换回原码就都是0了，没区别）

；

注意：无符号转成有符号数，而且还涉及长短位变化的时候，要留意这个顺序！！

一定是【先转换位数变化】，【再定义是无符号、还是有符号】