第十七节:图像梯度与边缘检测-Sobel 算子
一、引言:图像处理中的边缘奥秘
在数字图像处理领域,边缘检测是一项基础且关键的技术。人类的视觉系统能够在瞬间识别物体的轮廓,这种能力源于大脑对图像边缘信息的快速处理。在计算机视觉中,边缘检测同样扮演着重要角色,它是图像分割、目标识别、场景理解等高级任务的基础。而实现这一功能的核心工具之一,正是由Irwin Sobel在1968年提出的Sobel算子。

二、图像梯度与边缘的数学本质
2.1 图像函数的数学表示
将二维数字图像视为离散函数f(x,y),其中(x,y)表示像素坐标,函数值代表该点的灰度强度。对于彩色图像,可以分别处理每个颜色通道。
2.2 梯度的数学定义
在连续数学中,梯度是一个向量:
∇f = [∂f/∂x, ∂f/∂y]^T
其方向指向最大变化率方向,模长表示变化强度:
|∇f| = √((∂f/∂x)^2 + (∂f/∂y)^2)
2.3 离散域中的梯度计算
在离散图像中,偏导数通过差分近似:
G_x = f(x+1,y) - f(x-1,y)
G_y = f(x,y+1) - f(x,y-1)
这种中心差分法相比前向/后向差分具有更高的精度,计算复杂度为O(n),适用于实时处理。

三、Sobel算子的核心原理
3.1 卷积核的构造艺术
Sobel算子的精妙之处在于其独特的卷积核设计:
水平方向核:
[ -1 0 +1 ]
[ -2 0 +2 ]
[ -1 0 +1 ]垂直方向核:
[ +1 +2 +1 ]
[ 0 0 0 ]
[ -1 -2 -1 ]3.2 设计原理深度解析
-
权重分配:中间行(列)赋予更高的权重(系数2),增强当前像素的贡献
-
平滑处理:纵向/横向的平滑操作有效抑制噪声干扰
-
方向分离:水平和垂直核正交设计,实现各向异性检测
3.3 数学推导过程
考虑图像函数f(x,y)在3x3邻域内的近似泰勒展开:
f(x+1,y+1) ≈ f(x,y) + fx + fy + fxy + ...通过线性组合不同位置的差分,可以得到优化的导数估计公式。Sobel核实质上是加权平均的差分算子,在频域表现为带通滤波器。
四、算法实现与优化策略
4.1 基于OpenCV的Python实现
import cv2
import numpy as npdef sobel_edge_detection(image_path, ksize=3, threshold=100):# 读取图像并转换为灰度图img = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)# Sobel梯度计算Gx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=ksize)Gy = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=ksize)# 计算梯度幅值和角度mag = np.sqrt(Gx**2 + Gy**2)angle = np.arctan2(Gy, Gx) * 180 / np.pi# 归一化并应用阈值mag = cv2.normalize(mag, None, 0, 255, cv2.NORM_MINMAX)_, edges = cv2.threshold(mag, threshold, 255, cv2.THRESH_BINARY)return edges.astype(np.uint8)4.2 关键参数优化指南
-
卷积核尺寸(ksize):
-
3x3:基础版本,保留细节但易受噪声影响
-
5x5:增强平滑效果,适合高噪声环境
-
特殊值-1:使用Scharr算子(优化版3x3核)
-
-
阈值选择:
-
自适应阈值法(如Otsu)
-
双阈值法:低阈值保留弱边缘,高阈值确定强边缘
-
动态调节:根据图像内容自动调整
-
-
非极大值抑制:
沿梯度方向比较相邻像素,仅保留局部最大值

4.3 计算优化技巧
-
分离卷积:将2D卷积分解为行列1D卷积,计算复杂度从O(n^2)降为O(n)
-
并行计算:利用GPU或SIMD指令加速
-
积分图像:预计算积分图加速大核卷积
五、Sobel算子的变体与改进
5.1 Scharr算子
优化后的3x3核,具有更好的旋转对称性:
Gx = [[ -3 0 +3 ],[-10 0 +10],[ -3 0 +3 ]]Gy = [[ -3 -10 -3 ],[ 0 0 0 ],[ +3 +10 +3 ]]5.2 扩展Sobel算子
-
各向异性Sobel:调整核权重以适应特定方向
-
多尺度Sobel:不同尺度核的结果融合
-
彩色空间扩展:在HSV空间处理亮度分量
5.3 抗噪改进方案
-
高斯预处理:σ=0.5-1.0的高斯模糊
-
中值滤波:保持边缘的噪声消除
-
双边滤波:空间域和值域联合滤波
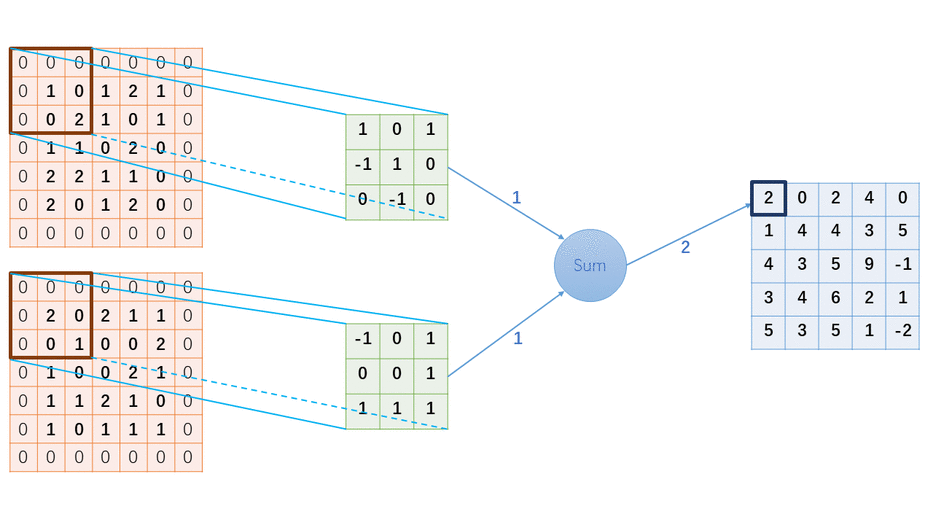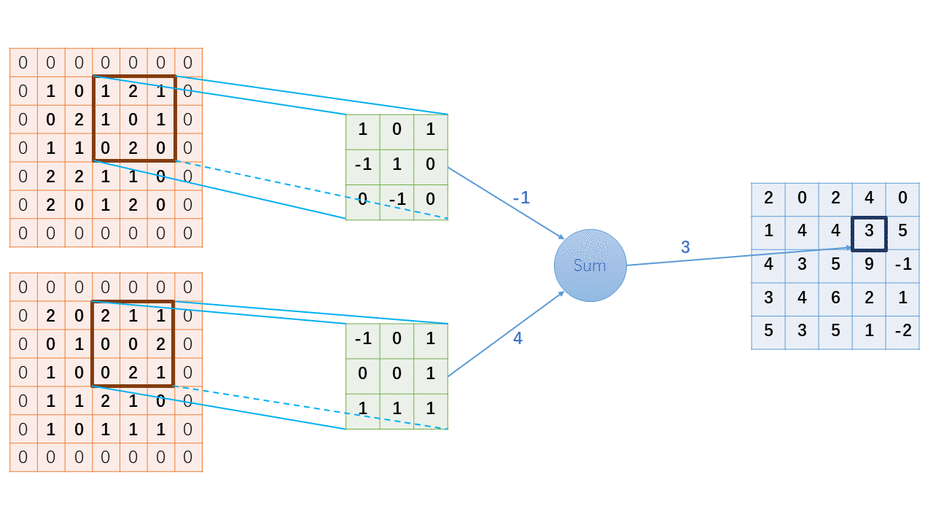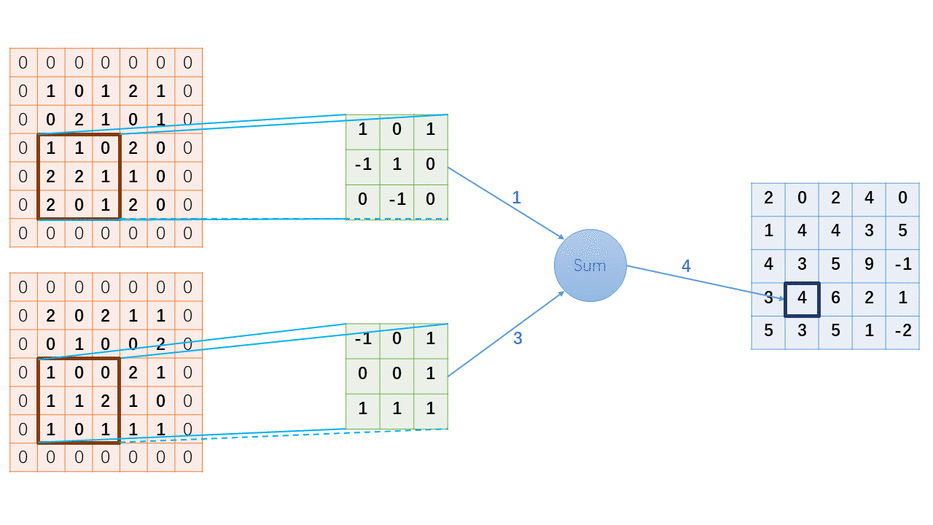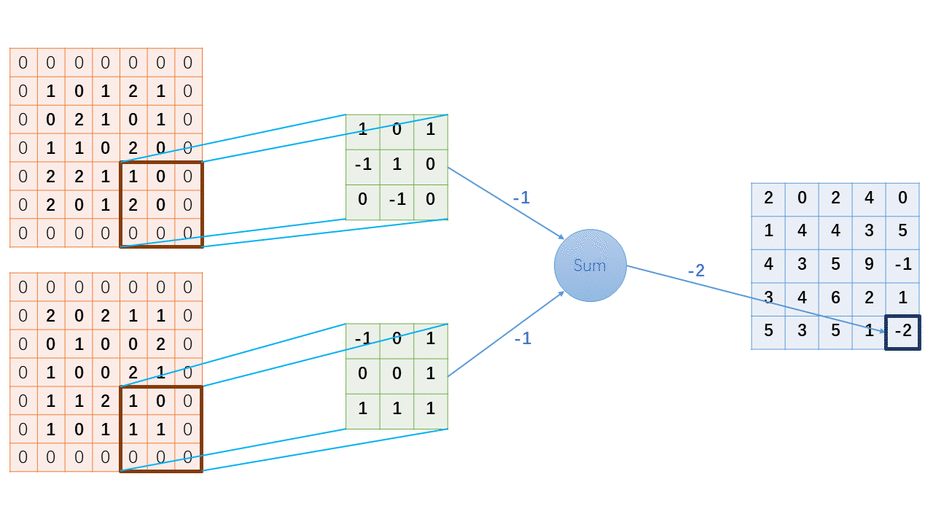
六、性能评估与对比分析
6.1 客观评价指标
-
Pratt品质因数:FOM = 1/(max(I,I')) * Σ1/(1+αd²)
-
边缘连续性:统计断裂边缘数量
-
抗噪指数:PSNR随噪声水平的变化率
6.2 主流算子对比
| 特性 | Sobel | Prewitt | Roberts | Canny |
|---|---|---|---|---|
| 计算复杂度 | 低 | 低 | 最低 | 高 |
| 抗噪能力 | 中 | 低 | 低 | 高 |
| 边缘定位 | 较好 | 一般 | 差 | 优秀 |
| 参数敏感性 | 低 | 低 | 低 | 高 |
| 实时性 | 优秀 | 优秀 | 优秀 | 一般 |
6.3 典型应用场景对比
-
实时视频处理:优先选择Sobel
-
医学图像分析:Canny结合形态学处理
-
工业检测:自适应Sobel改进算法
-
移动端应用:优化后的Scharr算子

七、工程实践中的挑战与解决方案
7.1 光照不均问题
-
同态滤波:压缩亮度动态范围
-
Retinex算法:估计光照分量
-
局部对比度归一化
7.2 复杂纹理干扰
-
Gabor滤波器组预处理
-
多分辨率分析(小波变换)
-
纹理抑制算子
7.3 弱边缘检测
-
相位一致性边缘检测
-
各向异性扩散增强
-
马尔可夫随机场建模

八、前沿发展与未来展望
8.1 深度学习边缘检测
-
HED(Holistically-Nested Edge Detection)
-
RCF(Rich Feature Hierarchies)
-
基于GAN的边缘检测框架
8.2 量子图像处理
-
量子Sobel算子模拟
-
量子傅里叶变换加速
-
量子并行计算实现
8.3 仿生视觉芯片
-
脉冲神经网络实现
-
视网膜形态电路设计
-
光流计算一体化
九、结语:传统算法的现代生命力
尽管深度学习在边缘检测领域取得了显著进展,Sobel算子依然保持着强大的生命力。其简洁的数学形式、高效的计算特性以及良好的可解释性,使其在嵌入式系统、实时处理、教学研究等领域不可替代。
