介绍最前沿的人工智能创新,‘无反向传播’神经网络训练方法?

图像由 Google ImageFX 生成
前言:
📌 本文整理自 NoProp 原始论文与实践代码,并结合多个公开实现细节进行了全流程复现。
🔍 对神经网络训练机制的探索仍在不断演进,如果你也在研究反向传播之外的新路径,这篇内容可能会给你一些启发。
正文:
反向传播(Backpropagation)首次出现在 1986 年,是如今几乎所有主流机器学习模型训练背后的关键算法之一。
它简单,容易实现,而且在训练大规模神经网络时效果很好。
不过,尽管被广泛接受为最优方法,它还是有一些明显的缺点,比如训练时内存占用高、以及因为算法是顺序执行的,难以实现并行训练。
那有没有一种算法,可以有效训练神经网络,又不带这些缺点?
牛津大学的一个研究团队刚刚提出了这样一种算法,它直接把反向传播给淘汰了。
他们的算法叫做 NoProp,甚至连前向传播都不需要,它基于扩散模型(Diffusion models)的原理,可以在不传递梯度的情况下,独立训练神经网络的每一层。
我们接下来就要深入探索这个算法的工作机制,对比其效果,还会从零开始写代码训练一个神经网络。
走起!
但首先,啥是反向传播?
MLP(多层感知机,Multi-Layer Perceptron)是全连接前馈型的深度神经网络,是今天所有 AI 技术的核心结构。
它们由一种叫“神经元”的单元组成。

神经元内部结构,是 MLP 的基本单位
神经元被堆叠成多层,在 MLP 中,一层的每个神经元都会和下一层的每个神经元相连接。

MLP 中连接方式的示意图
训练时,输入数据会穿过这些神经网络,每一层会对它施加权重、偏置和激活函数,逐层处理,最终在最后一层输出结果或预测。
这个过程叫作 前向传播(Forward pass 或 Forward propagation)。

前向传播的可视化
接下来,前向传播得到的输出会和输入数据对应的真实标签做比较,计算出误差或损失函数。
这时就轮到反向传播算法上场了,它会从最后一层开始,计算损失函数对网络参数(权重和偏置)的梯度。
这个过程通过微积分中的链式法则完成,并告诉我们每个参数对错误有多大贡献(也叫 credit assignment)。
这一步就叫 反向传播(Backward pass)。

反向传播的可视化
完成反向传播后,优化器会一层层更新/调整这些参数,以降低损失,从而让模型变得更优秀。
但反向传播的问题在哪?
尽管反向传播效果很好,但它对内存的消耗非常大。
你还记得前向传播时,每一层输出的结果吗?这些输出也叫作“中间激活值(Intermediate activations)”,它们必须被存储,因为后面做反向传播时还需要用到。
对于有几百层、上百万神经元的神经网络来说,训练时光是存这些中间激活值就可能占用好几个 GB 的 GPU 显存。
(确实有像“梯度检查点(Gradient checkpointing)”这种技术来缓解这个问题,但本质上还是很耗资源。)
此外,由于反向传播是顺序算法,每一层的梯度计算都依赖于下一层的梯度。
这意味着我们无法把所有层的梯度计算并行执行,每一层都得等下一层计算完自己那部分梯度,才能继续。
而且,用反向传播训练出来的神经网络,是按“分层方式”来学习的,也就是说,学习过程是分多个抽象层级的,低层学简单模式,高层在此基础上学更复杂的。
但当梯度从高层向低层传播时,不同任务或样本的数据更新有可能会互相干扰,甚至导致模型把以前学过的东西彻底忘掉(这个现象叫 灾难性遗忘 Catastrophic Forgetting)。
以下是之前出现过的一些反向传播替代方法,但都没太成功,因为它们在准确率、计算效率、可靠性或可扩展性方面表现不佳:
- Zero-order gradient methods
- Direct search gradient-free methods
- Model-based gradient-free methods
- Natural evolution strategies
- Difference Target Propagation
- Forward-Forward algorithm
那么,现在还可能有真正有效的“无反向传播学习”方法吗?
NoProp 来了
NoProp 算法借鉴了扩散模型(原本主要用在图像生成任务中的思路),把它用在了图像分类(监督学习)任务上。
如果你时间不多,想跳过数学细节,下面是这个算法的简略工作原理:
训练时,神经网络中的每一层/模块都会接收到一个带噪的标签和一个训练输入,然后它预测目标标签。
每一层都是独立训练的,使用的是一个去噪损失函数(denoising loss),这使得训练过程中完全不需要前向传播。
不过和训练不一样的是,在推理阶段,所有层是一起工作的。
从高斯噪声开始,每一层都会接收上一层生成的带噪标签,并将其去噪。
这个过程一层接一层进行,直到最终一层输出最终的真实类别(即完全去噪后的表示)。
接下来我们就要详细讲解这个算法的内部机制。
(如果你对扩散模型已经熟的话,看懂这一部分会更容易。)
假设我们有一个样本输入 x 和它的标签 y,我们的目标是训练一个模型,给定 x 预测出 y。
从数学角度讲,我们不是要找一个函数 f(x) = y,而是要训练一个神经网络,去建模一个从随机噪声转换成可估计 y 的形式的随机过程。
在这个过程中,有两个分布是需要理解的:
1. 随机前向/去噪过程
这个过程用 p 来表示,如下所示:

它建模了我们如何从噪声开始,经过一系列步骤,把它去噪到最终表示 z(T),然后用这个去预测标签 y。
数学上来说,它是所有中间噪声表示 z(0), …, z(T) 和标签 y 在给定输入 x 下的联合概率。
在这个公式里:
- p(z(0)) 表示标准高斯噪声
- p(z(t) ∣ z(t−1), x) 表示每一层是如何去噪输入噪声的
- p(y ∣ z(T)) 表示如何根据最终表示 z(T) 分类出 y
p(z(t) ∣ z(t−1), x) 是用神经网络参数化的,如下所示:

其中:
- 带参数 θ 的神经网络 û,乘上系数 a(t),根据带噪输入 z(t−1) 和 x 预测去噪后的表示
- b(t) ⋅ z(t−1) 是一个带权重的 skip connection(跳跃连接)
- √c(t) ⋅ ϵ(t) 是随机高斯噪声
- a(t), b(t), c(t) 是三个标量,用来分别给公式中的三项加权
2. 反向加噪过程 / 变分后验
这个过程用 q 表示,如下所示:

它建模了我们如何从标签 y(以它的嵌入 u(y) 的形式)开始,逐步加噪,直到得到 z(0)。
数学上来说,它是给定标签 y 和输入 x 下,最终带噪表示 z(T) 的概率分布。
在这个公式里:
- q(z(T) ∣ y) 表示给定标签 y 的表示 z(T)
- q(z(t−1) ∣ z(t)) 表示反向扩散过程,也就是通过加噪回到更早的噪声表示
q(z(T) ∣ y) 如下所给:

这表示这是一个关于潜变量 z(T) 的高斯分布,其中 √αˉ(T)⋅ u(y) 是均值,1 — αˉ(T) 是方差。
u(y) 是标签嵌入,αˉ(T) 表示在加噪过程中 u(y) 还剩多少。
q(z(t−1) ∣ z(t)) 给出如下公式:

这表示这是一个关于潜变量 z(t-1) 的高斯分布,其中 √α(t-1)⋅ z(t) 是均值,1 — α(t-1) 是方差。
α(t−1) 是一个噪声调度参数,控制在 t-1 这个时间步上保留了多少原始信号。
注意,α 和 αˉ 都来自一个固定的 cosine 噪声调度表。
定义损失函数
NoProp 算法的训练目标是最大化正确标签的对数似然 log p(y∣x)。
但直接优化这个 log-likelihood 是计算上不可行的,因为这需要对所有可能的高维潜变量 z(0), … , z(T) 积分。
作为替代方案,我们最大化它的一个变分下界,叫作 Evidence Lower Bound (ELBO)。


NoProp 的损失函数就是从这个表达式导出的:

(这个推导的数学细节写在原始论文的 A.4 节里。)
这公式看起来很复杂,其实挺容易懂的。
公式右边:
- 第一项是 交叉熵损失,衡量最终的表示 z(T) 用来预测标签 y 的准确程度;
- 第二项是 KL 散度,衡量起始表示 z(0) 和标准高斯噪声分布的差异。这是正则项,让这两个分布更像,从而保证扩散过程能正常运行;
- 第三项是 逐层去噪损失,衡量每一层的去噪效果,就是看它输出跟真实标签嵌入(L2 损失)之间的距离。
公式中,η 是超参数,SNR 是信噪比,定义如下:

随着 t 增加(即我们向网络更深的层前进),信号增强(噪声减少),因此 SNR 增加。
这意味着网络在后面层的错误会受到更大的惩罚。
🔧 有不少工程实践者已经在 NoProp 的基础上尝试将其应用到低功耗设备、边缘部署甚至大模型蒸馏中,这类探索也正在成为 AI 推理优化的新方向。
🧠 对这些实际落地案例感兴趣的朋友,可以进一步参考一些工程笔记和复现流程图。
训练过程
训练时,网络学的是:在每一层上把带噪的标签嵌入给去噪掉,而不需要完整的前向或反向传播。
对于一个输入-标签对 (x, y),一个嵌入矩阵 W(embed) 会把标签 y 映射成嵌入 u(y),矩阵的每一行就是标签 y 的嵌入。
首先,我们给 u(y) 加上噪声,变成 z(t)。
然后,每一层的神经网络 û(θ)(z(t−1) , x) 都独立训练,学习如何根据输入 x 和上一层的带噪表示 z(t-1) 来预测干净的嵌入 u(y)。
训练损失被计算出来,使用优化器最小化这个损失来更新网络参数。
训练算法总结如下伪代码所示:

推理过程
推理阶段,总共有 T 层/模块的网络会接收到高斯噪声 z(0)。
每一层从 z(0) 开始,接收上一层的输出 z(t-1) 和输入 x,生成下一层的去噪表示 z(t)。
这个过程逐层进行,形成每一层的中间表示 z(0), z(1), …, z(t), z(T-1), z(T)。
最终一步 t = T,输出 z(T) 会被送入分类器,预测最终标签 ŷ。
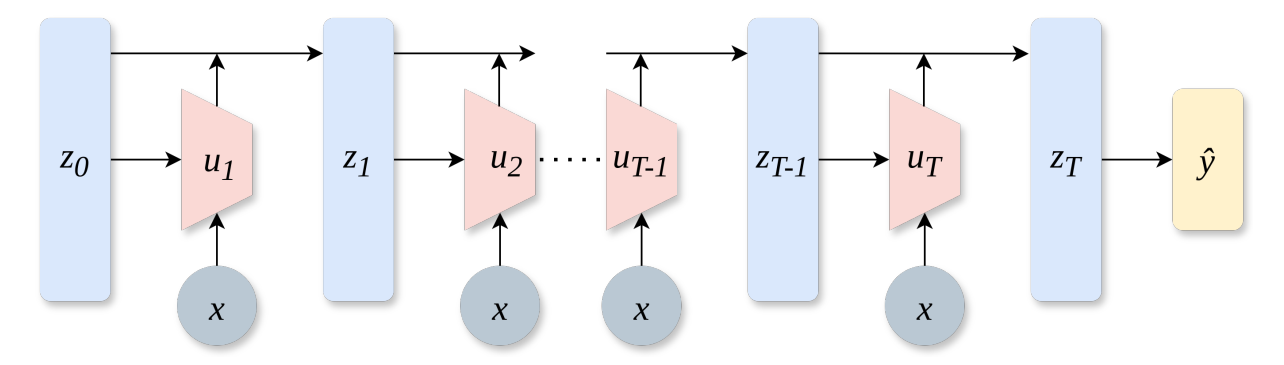
z(0) 被每一层依次转化为 z(T),每一层都表示为 u(t),条件是输入 x,最终得到预测标签 ŷ。
层/模块结构
每一层/模块 û(θ)(z(t−1) , x),如上所述,是一个复杂的神经网络,它接受:
- 输入 x,通过卷积嵌入模块处理,然后接入一个全连接层;
- 上一层的带噪表示 z(t-1),通过带 skip connection 的全连接网络处理;
这些输入会被送入额外的全连接层,生成 logits。
logits 再通过 softmax 函数,变成一个对类别嵌入的概率分布。
最终输出是用这个概率分布对类别嵌入加权求和得到的。

每一层/模块的结构,如上一图中所示的 u(t)
NoProp 的表现到底咋样?
我们上面讲的是 NoProp 的离散时间(Discrete-Time, DT)版本,也叫 NoProp-DT。
它之所以叫这个名字,是因为它模拟的是一个离散时间步的扩散过程,而不是连续的。
这个算法还有两个变种,分别是:
- NoProp-CT(Continuous-Time):这个版本用的是连续的噪声调度,整个扩散过程是连续时间范围内进行的,不是一步一步离散的。
- NoProp-FM(Flow Matching):这个版本不是通过去噪,而是通过**常微分方程(ODE)**学习一个向量场,把噪声引导到预测标签嵌入那边。
这几个版本都在图像分类任务上,和反向传播以及其他非反向传播方法进行了比较,数据集用的是这三个常见的 benchmark:
- MNIST:共 70,000 张手写数字灰度图(每张 28x28 像素),共 10 个类别(0–9)
- CIFAR-10:共 60,000 张彩色图(每张 32x32 像素),有 10 个物体类别
- CIFAR-100:共 60,000 张彩色图(每张 32x32 像素),共有 100 个物体类别
实验表明,NoProp 在这三组数据集上的表现都和反向传播一样好,甚至更好,而且也优于之前那些无反向传播的算法。

不同训练方法在 MNIST 和 CIFAR 数据集上的分类准确率
除此之外,NoProp 在训练时还比其他方法用更少的 GPU 显存。

不同方法在训练时所分配的 GPU 显存
手写实现 NoProp
既然我们已经搞清楚 NoProp 的理论部分,现在就自己写代码跑一遍试试看。
全部代码用 PyTorch 写在 Jupyter Notebook 里,方便阅读和运行。
安装依赖
如果你是在 Google Colab 上跑的话,不需要安装这些。
!uv pip install torch torchvision matplotlib
使用 GPU / Apple MPS(如果有的话)
# 设置设备
if torch.backends.mps.is_available():
device = "mps"
elif torch.cuda.is_available():
device = "cuda"
else:
device = "cpu"
print("Using device:", device)
定义去噪模块
这是我们的去噪神经网络模块(û(θ)),它接受三个输入:
- 一张图像 x
- 一个带噪的中间表示 z(t-1)
- 一个类嵌入矩阵 W_embed,其中每一行是标签的嵌入 u(y)
这个模块学的是:怎样根据图像 x 把 z(t-1) 去噪,尽量还原成真实的标签嵌入 u(y)。
它输出下一步表示 z(t)。
和普通神经网络不一样的是,这些模块是独立训练的,每层各干各的。
# Denoising block
class DenoiseBlock(nn.Module):
def __init__(self, embedding_dim, num_classes):
super().__init__()
# 图像路径
self.conv_path = nn.Sequential(
nn.Conv2d(1, 32, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Dropout(0.2),
nn.Conv2d(32, 64, 3, padding=1),
nn.ReLU(),
nn.Dropout(0.2),
nn.Conv2d(64, 128, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Dropout(0.2),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(),
nn.Linear(128, 256),
nn.BatchNorm1d(256)
)
# 噪声嵌入路径
self.fc_z1 = nn.Linear(embedding_dim, 256)
self.bn_z1 = nn.BatchNorm1d(256)
self.fc_z2 = nn.Linear(256, 256)
self.bn_z2 = nn.BatchNorm1d(256)
self.fc_z3 = nn.Linear(256, 256)
self.bn_z3 = nn.BatchNorm1d(256)
# 融合路径
self.fc_f1 = nn.Linear(256 + 256, 256)
self.bn_f1 = nn.BatchNorm1d(256)
self.fc_f2 = nn.Linear(256, 128)
self.bn_f2 = nn.BatchNorm1d(128)
self.fc_out = nn.Linear(128, num_classes)
def forward(self, x, z_prev, W_embed):
# 图像特征
x_feat = self.conv_path(x)
# 噪声嵌入特征
h1 = F.relu(self.bn_z1(self.fc_z1(z_prev)))
h2 = F.relu(self.bn_z2(self.fc_z2(h1)))
h3 = self.bn_z3(self.fc_z3(h2))
z_feat = h3 + h1 # 残差连接
# 合并后预测 logits
h_f = torch.cat([x_feat, z_feat], dim=1)
h_f = F.relu(self.bn_f1(self.fc_f1(h_f)))
h_f = F.relu(self.bn_f2(self.fc_f2(h_f)))
logits = self.fc_out(h_f)
# Softmax + 嵌入加权
p = F.softmax(logits, dim=1)
z_next = p @ W_embed
return z_next, logits
定义 NoProp-DT 模型
这个模型把 T 步扩散过程中用到的多个 Denoising Blocks 组合起来,训练时不使用反向传播。
# NoProp-DT model
class NoPropDT(nn.Module):
def __init__(self, num_classes, embedding_dim, T, eta):
super().__init__()
self.num_classes = num_classes
self.embedding_dim = embedding_dim
self.T = T
self.eta = eta
# 堆叠多个 DenoiseBlock
self.blocks = nn.ModuleList([
DenoiseBlock(embedding_dim, num_classes) for _ in range(T)
])
# 类别嵌入矩阵(W_embed)
self.W_embed = nn.Parameter(torch.randn(num_classes, embedding_dim) * 0.1)
# 分类头
self.classifier = nn.Linear(embedding_dim, num_classes)
# Cosine 噪声调度
t = torch.arange(1, T+1, dtype=torch.float32)
alpha_t = torch.cos(t / T * (math.pi/2))**2
alpha_bar = torch.cumprod(alpha_t, dim=0)
snr = alpha_bar / (1 - alpha_bar)
snr_prev = torch.cat([torch.tensor([0.], dtype=snr.dtype), snr[:-1]], dim=0)
snr_diff = snr - snr_prev
self.register_buffer('alpha_bar', alpha_bar)
self.register_buffer('snr_diff', snr_diff)
def forward_denoise(self, x, z_prev, t):
return self.blocks[t](x, z_prev, self.W_embed)[0]
def classify(self, z):
return self.classifier(z)
def inference(self, x):
B = x.size(0)
z = torch.randn(B, self.embedding_dim, device=x.device)
for t in range(self.T):
z = self.forward_denoise(x, z, t)
return self.classify(z)
定义训练函数
这个函数是用来训练 NoProp-DT 模型的(本质是多个去噪模块的组合,训练中不使用反向传播)
# Function for training NoProp-DT
def train_nopropdt(model, train_loader, test_loader, epochs, lr, weight_decay):
optimizer = torch.optim.AdamW(model.parameters(), lr=lr, weight_decay=weight_decay)
history = {'train_acc': [], 'val_acc': []}
for epoch in range(1, epochs + 1):
model.train()
for t in range(model.T):
for x, y in train_loader:
x, y = x.to(device), y.to(device)
uy = model.W_embed[y]
alpha_bar_t = model.alpha_bar[t]
noise = torch.randn_like(uy)
z_t = torch.sqrt(alpha_bar_t) * uy + torch.sqrt(1 - alpha_bar_t) * noise
z_pred, _ = model.blocks[t](x, z_t, model.W_embed)
loss_l2 = F.mse_loss(z_pred, uy)
loss = 0.5 * model.eta * model.snr_diff[t] * loss_l2
if t == model.T - 1:
logits = model.classifier(z_pred)
loss_ce = F.cross_entropy(logits, y)
loss_kl = 0.5 * uy.pow(2).sum(dim=1).mean()
loss = loss + loss_ce + loss_kl
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
optimizer.step()
# 训练准确率
model.eval()
correct, total = 0, 0
with torch.no_grad():
for x, y in train_loader:
x, y = x.to(device), y.to(device)
preds = model.inference(x).argmax(dim=1)
correct += (preds == y).sum().item()
total += y.size(0)
train_acc = correct / total
# 验证准确率
val_correct, val_total = 0, 0
with torch.no_grad():
for x, y in test_loader:
x, y = x.to(device), y.to(device)
preds = model.inference(x).argmax(dim=1)
val_correct += (preds == y).sum().item()
val_total += y.size(0)
val_acc = val_correct / val_total
history['train_acc'].append(train_acc)
history['val_acc'].append(val_acc)
print(f"Epoch {epoch}/{epochs} "
f"TrainAcc={100 * train_acc:.2f}% ValAcc={100 * val_acc:.2f}%")
# 绘制准确率曲线
plt.figure()
plt.plot(range(1, epochs + 1), history['train_acc'], label='Train Accuracy')
plt.plot(range(1, epochs + 1), history['val_acc'], label='Validation Accuracy')
plt.title("Accuracy Curve")
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.legend()
plt.grid(True)
plt.show()
print(f"\n Final Test Accuracy: {100 * val_acc:.2f}%")
设置超参数
下面是作者在实验中使用的超参数设定:

我们只做了一点点调整:把训练轮数从 100 改成了 10,因为对本教程来说这个训练量已经够用了。
# Hyperparameters
T = 10
eta = 0.1
embedding_dim = 512
batch_size = 128
lr = 1e-3
epochs = 10
weight_decay = 1e-3
加载 MNIST 数据集
我们不会对 MNIST 数据集使用数据增强,这也是和原始研究论文中的实验设置保持一致。
# Loading MNIST
transform = transforms.ToTensor()
train_set = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_set = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
train_loader = DataLoader(train_set, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_set, batch_size=batch_size)
初始化模型
现在我们来用前面定义的超参数把模型初始化一下。
# Initializing model
model = NoPropDT(num_classes=10, embedding_dim=embedding_dim, T=T, eta=eta).to(device)
训练模型
准备好了!开训!
# Begin training
train_nopropdt(model, train_loader, test_loader, epochs=epochs, lr=lr, weight_decay=weight_decay)
训练结束后,我们拿到了 98.88% 的验证准确率!

可视化预测结果
我们来画出模型的预测结果看看效果。
# Function to plot predictions
def show_predictions(model, test_loader, class_names=None, num_images = 16):
model.eval()
images_shown = 0
plt.figure(figsize=(5, 5))
with torch.no_grad():
for x, y in test_loader:
x, y = x.to(device), y.to(device)
logits = model.inference(x)
preds = logits.argmax(dim=1)
for i in range(x.size(0)):
if images_shown >= num_images:
break
plt.subplot(int(num_images**0.5), int(num_images**0.5), images_shown + 1)
img = x[i].cpu().squeeze(0)
plt.imshow(img, cmap='gray')
actual = class_names[y[i]] if class_names else y[i].item()
pred = class_names[preds[i]] if class_names else preds[i].item()
plt.title(f"Pred: {pred}\nTrue: {actual}", fontsize=8)
plt.axis('off')
images_shown += 1
if images_shown >= num_images:
break
plt.tight_layout()
plt.show()
# Class names for MNIST dataset
class_names = [str(i) for i in range(10)]
# Visualising predictions
show_predictions(model, test_loader)

以上,就是关于 NoProp 算法 的这个教程的全部内容。后续我们将会关注这一人工智能领域的前沿研究的进展,为大家提供最新相关的资讯,敬请关注。
📩 我整理了一份《无反向传播训练方法实战笔记》,里面涵盖了 NoProp 的核心原理解析、PyTorch 复现结构图、以及工程落地建议(部署与资源控制)。如需获取,欢迎评论【NoProp笔记】或私信交流。
