GESP2024年6月认证C++八级( 第三部分编程题（2）空间跳跃）

参考程序：

#include <cstdio>
#include <vector>
#include <queue>
#include <utility>
#include <cstring>
using namespace std;// 定义一个结构体，用于 Dijkstra 优先队列中的节点
struct Node {int v, w; // v 表示图中的节点编号，w 表示当前从源点到 v 的最短距离bool operator < (const Node &b) const {// C++ 优先队列默认是大顶堆，这里重载为距离小的优先出队return w > b.w;}
};// 假设最多 n 个挡板，我们编号为 1..n
const int MAXN = 10010;  // 挡板数量上限（可根据题目数据范围调整）
const int INF = 2000000000;// 图的邻接表表示，每个节点存储 (目标节点, 权值) 对
vector<pair<int,int>> G[MAXN*2]; // 每个挡板有两个端点，编号方案见下// 存储挡板数据
int l[MAXN], r[MAXN], h[MAXN]; // l[i], r[i] 为挡板 i 的左右横坐标，h[i] 为高度
int n, s, t; // n 挡板个数，s 起点挡板编号，t 目标挡板编号// 将挡板编号转换为节点编号：例如取左端点编号 2*i，右端点编号 2*i+1
inline int LL(int x) { return 2*x; }
inline int RR(int x) { return 2*x+1; }// Dijkstra 算法求单源最短路
int dis[MAXN*2];
bool vis[MAXN*2];
void Dijkstra(int src) {// 初始化距离为无穷大，标记都为未访问for(int i = 0; i < 2*n+2; i++) {dis[i] = INF;vis[i] = false;}// 源点距离置 0，入队dis[src] = 0;priority_queue<Node> pq;pq.push({src, 0});while(!pq.empty()) {Node cur = pq.top(); pq.pop();int u = cur.v;if(vis[u]) continue; // 如果已访问，跳过vis[u] = true;// 遍历所有从 u 出发的边for(auto &edge : G[u]) {int v = edge.first;int w = edge.second;if(!vis[v] && dis[v] > dis[u] + w) {dis[v] = dis[u] + w; // 松弛pq.push({v, dis[v]});}}}
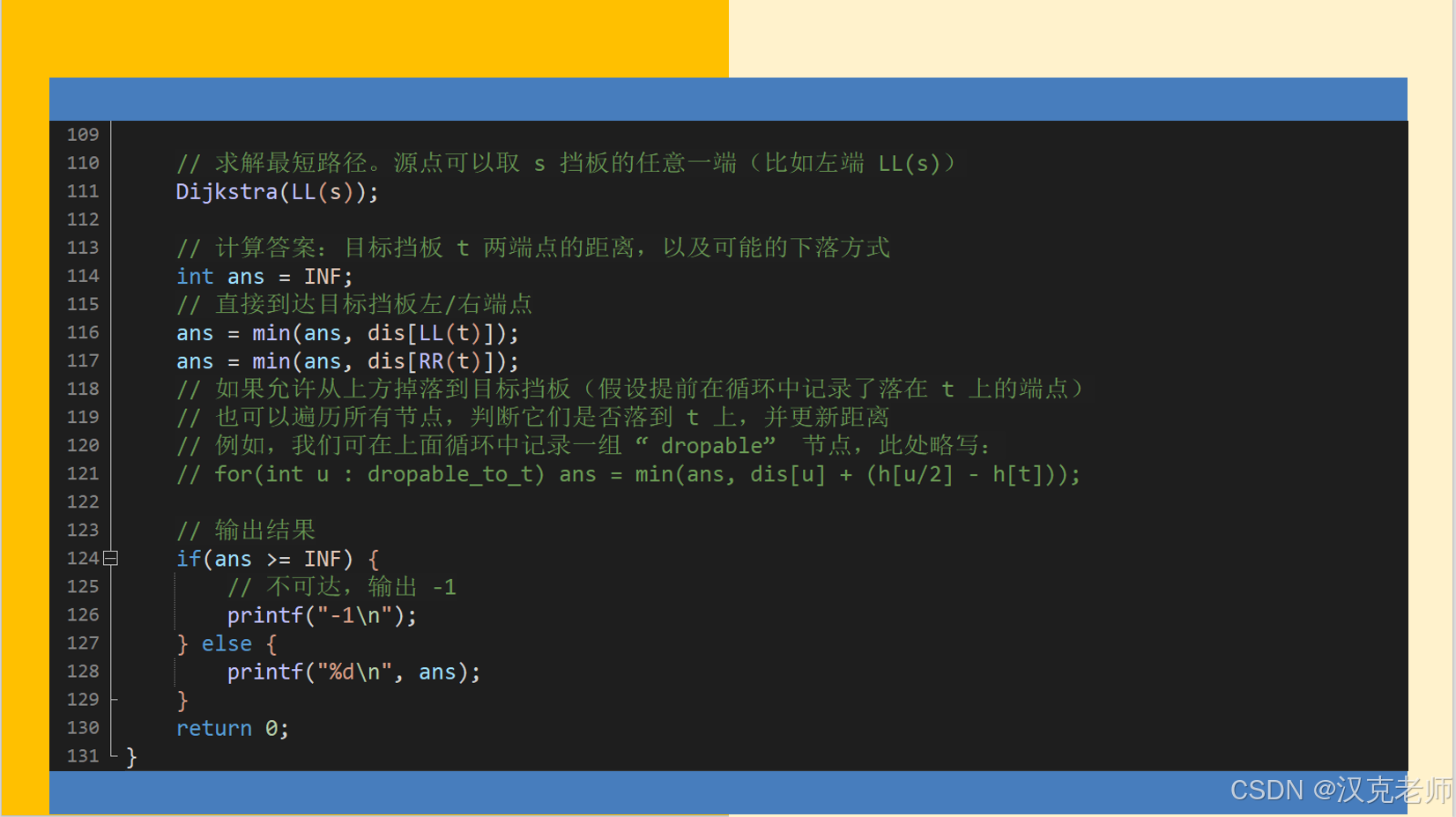
}int main(){// 读入挡板数量和起点、终点挡板编号scanf("%d %d %d", &n, &s, &t);// 读入每个挡板的左右坐标和高度for(int i = 1; i <= n; i++){scanf("%d %d %d", &l[i], &r[i], &h[i]);// 添加挡板 i 水平移动的双向边：左端到右端，权值为挡板长度G[LL(i)].push_back({RR(i), r[i] - l[i]}); G[RR(i)].push_back({LL(i), r[i] - l[i]});}// 以下构造竖直掉落的边，采用辅助节点思路或直接加边思路任选其一// 这里以直接连边（两条边）为例：// 对于每个挡板 i 的左端点和右端点，找到其下方第一个挡板 j// 可以用两重循环暴力检查（效率 O(n^2)），寻找最低高度却高于 i 的挡板// 或者按照高度排序后逐一处理。此处示意逻辑：for(int i = 1; i <= n; i++){// 初始化记录，第一个落点挡板索引int dropL = 0, dropR = 0;for(int j = 1; j <= n; j++){if(h[j] < h[i]) { // 下方的挡板// 左端点下落：如果挡板 j 横跨了 i 的左端点位置if(l[i] >= l[j] && l[i] <= r[j]) {// 取最近的挡板（高度最大的）if(dropL == 0 || h[j] > h[dropL]) dropL = j;}// 右端点下落：如果挡板 j 横跨了 i 的右端点位置if(r[i] >= l[j] && r[i] <= r[j]) {if(dropR == 0 || h[j] > h[dropR]) dropR = j;}}}// 如果找到了下方挡板，则添加掉落边if(dropL != 0) {int dh = h[i] - h[dropL]; // 竖直高度差// 从 i 的左端点掉落到 dropL 左端点、右端点G[LL(i)].push_back({LL(dropL), dh + (l[i] - l[dropL])});G[LL(i)].push_back({RR(dropL), dh + (l[dropL] + (r[dropL]-l[dropL]) - l[i])});}if(dropR != 0) {int dh = h[i] - h[dropR];// 从 i 的右端点掉落到 dropR 左端点、右端点G[RR(i)].push_back({LL(dropR), dh + (r[i] - l[dropR])});G[RR(i)].push_back({RR(dropR), dh + (r[dropR] - r[i])});}}// 求解最短路径。源点可以取 s 挡板的任意一端（比如左端 LL(s)）Dijkstra(LL(s));// 计算答案：目标挡板 t 两端点的距离，以及可能的下落方式int ans = INF;// 直接到达目标挡板左/右端点ans = min(ans, dis[LL(t)]);ans = min(ans, dis[RR(t)]);// 如果允许从上方掉落到目标挡板（假设提前在循环中记录了落在 t 上的端点）// 也可以遍历所有节点，判断它们是否落到 t 上，并更新距离// 例如，我们可在上面循环中记录一组 “dropable” 节点，此处略写：// for(int u : dropable_to_t) ans = min(ans, dis[u] + (h[u/2] - h[t]));// 输出结果if(ans >= INF) {// 不可达，输出 -1printf("-1\n");} else {printf("%d\n", ans);}return 0;
}