MobileNetV2: 反向残差和线性瓶颈

摘要

本文提出了一种新的移动端架构 MobileNetV2，它在多个任务和基准测试上提升了移动模型的性能，并涵盖了不同模型尺寸的范围。我们还提出了一种高效的方式将这些移动模型应用于目标检测，并构建了一个新框架，称为 SSDLite。此外，我们还展示了如何通过一种简化的 DeepLabv3 形式（我们称之为 Mobile DeepLabv3）构建移动端的语义分割模型。

该架构基于一种倒残差结构，其中快捷连接发生在瘦的 bottleneck 层之间。中间的扩展层使用轻量的 depthwise 卷积来对特征进行滤波，从而引入非线性。此外，我们发现，为了保持表达能力，在窄层中去除非线性变换是很重要的。我们证明了这种做法可以提升性能，并提供了我们采用此设计的直觉解释。

最后，我们的方法使输入/输出域与变换表达能力解耦，从而提供了一个便于进一步分析的框架。我们在 ImageNet [1] 分类、COCO 目标检测 [2]、VOC 图像分割 [3] 上对模型性能进行了测量。我们评估了准确率与 multiply-adds（MAdd）计算量、实际延迟、参数数量之间的权衡。

1. 引言

神经网络已经在许多机器智能领域引发了革命，使得在挑战性的图像识别任务中实现了超越人类的准确率。然而，提升准确率的驱动常常伴随着高昂的代价：当前最先进的网络需要高计算资源，这超出了许多移动端和嵌入式应用的承载能力。

本文引入了一种专为移动和资源受限环境设计的新型神经网络架构。我们的网络推动了面向移动端的计算机视觉模型的前沿，显著减少了运算量和内存需求，同时保持了相同的准确率。

我们的主要贡献是一种新颖的层模块：倒残差结构与线性 bottleneck。该模块以一个低维压缩表示作为输入，首先将其扩展到高维，然后通过轻量级 depthwise 卷积进行特征滤波。随后，特征再通过线性卷积投影回低维表示。官方实现作为 TensorFlow-Slim 模型库的一部分提供于 [4]。

该模块可以使用任何现代框架中的标准操作高效实现，使我们的模型在多个性能点上都能超越当前最优结果，并且可以在标准基准上评估。此外，这种卷积模块特别适合移动端设计，因为它可以显著减少推理时的内存占用，避免完整地生成大型中间张量。这减少了许多嵌入式硬件设计中对主存访问的需求，这些硬件通常只提供少量、由软件控制的高速缓存内存。

2. 相关工作

近年来，调优深度神经网络结构以在准确率与性能之间实现最佳平衡一直是一个活跃的研究领域。无论是手动架构搜索还是训练算法的改进，由多个团队推动的研究均显著超越了早期的设计，例如 AlexNet [5]、VGGNet [6]、GoogLeNet [7] 和 ResNet [8]。近期，算法架构探索取得了大量进展，包括超参数优化 [9, 10, 11]，以及各种网络剪枝方法 [12, 13, 14, 15, 16, 17] 和连接学习方法 [18, 19]。也有大量工作致力于改变内部卷积块的连接结构，例如 ShuffleNet [20]、引入稀疏性的方法 [21] 以及其他方法 [22]。

近期，[23, 24, 25, 26] 打开了一个新方向，即将优化方法（包括遗传算法和强化学习）引入架构搜索中。但该类方法的一大缺点是结果网络非常复杂。本文追求的目标是发展对神经网络如何运作的更好直觉，并据此指导出最简单可能的网络设计。我们的方法应被视为对 [23] 及相关工作的互补。

从这个角度来看，我们的方法类似于 [20, 22] 所采用的方法，能够进一步提升性能，同时提供对其内部操作的洞见。我们的网络设计基于 MobileNetV1 [27]，保留了其简洁性，并且不需要任何特殊操作符，同时显著提升了准确率，在多个面向移动端的图像分类和检测任务上实现了最先进的性能。

3. 预备知识、讨论与直觉

3.1. Depthwise Separable Convolutions

Depthwise Separable Convolutions 是许多高效神经网络结构中的关键构建模块 [27, 28, 20]，我们在本工作中也采用了这一方法。其基本思想是用一个分解的版本来替代完整的卷积操作，该分解版本将卷积分为两个独立的层。第一层称为 depthwise 卷积，它通过对每个输入通道应用单一的卷积核进行轻量级的特征滤波。第二层是一个 $1\times 1$ 卷积，称为 pointwise 卷积，它负责通过对输入通道进行线性组合来构建新的特征。

标准卷积操作作用于一个大小为 $h_i\times w_i\times d_i$ 的输入张量 $L_i$，并使用卷积核 ${\mathcal{R}}^{k\times k\times d_i\times d_j}$ 进行卷积，以产生一个大小为 $h_i\times w_i\times d_j$ 的输出张量 $L_j$。标准卷积层的计算成本为：$h_i\cdot w_i\cdot d_i\cdot d_j\cdot k\cdot k$

Depthwise separable convolutions 可以直接替代标准卷积层。在实际中，它们的效果几乎与普通卷积相当，但计算成本仅为：

$$h_i\cdot w_i\cdot d_i(k^2+d_i)\text{\hspace{1em}(1)}$$

这是 depthwise 卷积与 $1\times 1$ pointwise 卷积的计算成本之和。实际上，depthwise separable convolution 将计算量相比传统卷积减少了近 $k^2$ 倍。MobileNetV2 使用 $k=3$（即 $3\times 3$ 的 depthwise separable convolutions），因此其计算成本比标准卷积小 8 到 9 倍，而准确率仅有轻微下降 [27]。

3.2. Linear Bottlenecks

考虑一个包含 $n$ 层 $L_i$ 的深度神经网络，其中每一层都有大小为 $h_i\times w_i\times d_i$ 的激活张量。在本节中，我们将讨论这些激活张量的基本性质，并将其视为包含 $h_i\times w_i$ 个 “像素”，每个像素具有 $d_i$ 维度的容器。非正式地说，对于一组输入真实图像，我们认为每一层 $L_i$ 的激活集合构成一个 “感兴趣的流形（manifold of interest）”。长期以来人们一直认为，神经网络中的这些感兴趣流形可以嵌入到低维子空间中。换句话说，当我们查看深度卷积层中所有的 $d$ 通道像素时，其所包含的信息实际位于某个流形上，该流形又可嵌入到某个低维子空间中[^2]。

乍一看，这一事实似乎可以通过简单地降低某层的维度来捕捉和利用，从而减少操作空间的维度。这一思路已被 MobileNetV1 [27] 成功利用，通过一个 width multiplier 参数在计算量和准确率之间进行权衡，同时也被其他网络的高效模型设计采用 [20]。依据这一直觉，width multiplier 方法允许我们缩减激活空间的维度，直到感兴趣的流形完全覆盖该空间。然而，这一直觉在考虑深度卷积神经网络实际上包含坐标级非线性变换（如 ReLU）时就会失效。例如，ReLU 应用于一维空间中的一条直线会得到一个 “射线（ray）”；而在 $R^n$ 空间中，则通常产生一个带有 $n$ 个连接点的分段线性曲线。

我们可以很容易看出，如果某一层的变换结果 $ReLU(Bx)$ 的非零体积为 $S$，那么落入 $S$ 内部的点是通过输入的线性变换 $B$ 得到的，这就说明输出空间中具有完整维度的部分，其对应的输入空间仅经过了线性变换。换言之，深度网络在输出域非零体积的部分，仅具有线性分类器的能力。更形式的描述请参考补充材料。

另一方面，当 ReLU 使某个通道坍缩（collapse）时，它不可避免地会丢失该通道中的信息。然而，如果我们拥有大量通道，并且激活流形中存在某种结构，那么这些信息可能仍然会在其他通道中被保留。在补充材料中，我们展示了：如果输入流形可以嵌入到激活空间的一个显著低维的子空间中，那么 ReLU 变换在引入表达函数所需复杂性的同时，仍然能够保留信息。

总结来说，我们强调了两个表征性质，它们指出了一个前提条件：感兴趣的流形应当位于高维激活空间的某个低维子空间中：

1. 如果感兴趣的流形在 ReLU 变换后仍保持非零体积，则其对应的是一个线性变换。
   

2. ReLU 能够保留关于输入流形的完整信息，但前提是输入流形位于输入空间的某个低维子空间中。

这两个洞察为我们提供了一个优化现有神经网络架构的经验性提示：假设感兴趣的流形是低维的，我们可以通过在卷积模块中插入 linear bottleneck 层来捕捉这种结构。实验结果表明，使用线性层是至关重要的，因为它可以防止非线性变换丢失过多信息。在第 6 节中，我们通过实证结果展示了，在 bottleneck 中使用非线性层确实会使性能下降几个百分点，从而进一步验证了我们的假设3^3。我们注意到，[29] 中也报告了类似的现象：当将非线性从传统 residual block 的输入中移除时，在 CIFAR 数据集上带来了性能提升。

在本文的其余部分中，我们将采用 bottleneck convolution。我们将输入 bottleneck 的尺寸与内部尺寸之间的比值称为 expansion ratio。

3.3. Inverted residuals

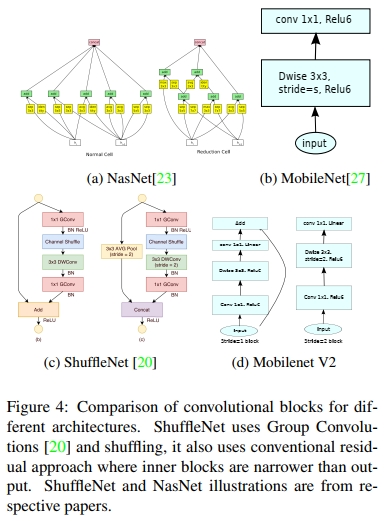
bottleneck block 看起来类似于 residual block，其中每个 block 包含一个输入，随后是多个 bottleneck，再之后是 expansion [8]。然而，受以下直觉启发：bottleneck 实际上包含了所有必要的信息，而 expansion 层仅作为伴随 tensor 非线性变换的实现细节，我们在 bottleneck 之间直接使用 shortcut。图 3 给出了不同设计方案的示意图。插入 shortcut 的动机与传统 residual connection 类似：我们希望提升梯度在多个层之间传播的能力。然而，这种反转设计在我们的实验中不仅内存效率更高（详见第 5 节），而且表现略好。

bottleneck convolution 的运行时间和参数数量
其基本实现结构如表 1 所示。对于尺寸为 $h\times w$、扩展因子为 $t$、卷积核大小为 $k$，输入通道为 $d^{\prime }$，输出通道为 $d^{\prime \prime }$ 的 block，总的乘加次数为：

$$h\cdot w\cdot d^{\prime }\cdot t(d^{\prime }+k^2+d^{\prime \prime })$$

与公式（1）相比，该表达式多了一个项，因为我们确实多了一个 $1\times 1$ 卷积。不过，由于我们网络的结构设计，可以使用更小的输入和输出维度。在表 3 中，我们比较了在各分辨率下 MobileNetV1、MobileNetV2 和 ShuffleNet 所需的尺寸。

3.4. 信息流解释

我们架构的一个有趣性质是：它在构建模块（即 bottleneck 层）的输入/输出域与层变换之间提供了天然的分离 —— 层变换是将输入转为输出的非线性函数。前者可以被视为网络在每一层的容量，后者则为其表达能力。这一点不同于传统的卷积 block（无论是 regular 还是 separable），传统结构中表达能力与容量是纠缠在一起的，并且都是输出通道数的函数。

具体来说，在我们的结构中，当中间层深度为 $O$ 时，得益于 shortcut connection，其底层卷积就是恒等函数。当 expansion ratio 小于 1 时，这是一个经典的 residual convolutional block [8, 30]。然而，对我们的目标来说，我们展示了 expansion ratio 大于 1 是最有用的。

这一解释让我们能够将网络的表达能力与其容量分开研究，我们认为对这种分离的进一步探索，有望带来对网络性质更深入的理解。

4. Model Architecture

现在我们将详细描述我们的架构。如上一节所述，基本构建模块是带有 residual 的 bottleneck depth-separable convolution。该 block 的详细结构如表 1 所示。MobileNetV2 的整体架构包含一个初始的全卷积层，使用 32 个 filter，随后是表 2 中描述的 19 个 residual bottleneck layer。

我们使用 ReLU6 作为非线性激活函数，因为在低精度计算环境下它表现得更为稳健 [27]。我们始终使用核大小为 $3\times 3$，这是现代网络的标准设置，并在训练过程中使用 dropout 和 batch normalization。

除了第一层之外，我们在整个网络中使用恒定的 expansion rate。在实验中我们发现，expansion rate 在 5 到 10 之间时性能曲线几乎没有区别：对于较小的网络，稍小的 expansion rate 表现更好，而较大的网络在使用较大的 expansion rate 时性能略优。

在我们所有主要实验中，均使用 expansion factor 为 6，并应用于输入 tensor 的大小。例如，对于一个 bottleneck layer，其输入 tensor 为 64 个通道，输出为 128 个通道，则中间的 expansion layer 将为 $64\cdot 6=384$ 个通道。

Trade-off 超参数 如同 [27]，我们通过调整输入图像分辨率和 width multiplier 这两个可调超参数，来将架构适配到不同的性能需求点，这两个参数可根据期望的精度/性能权衡进行调节。我们的主力网络（width multiplier 为 1，输入分辨率为 $224\times 224$）具有 3 亿次 multiply-adds 的计算成本，使用了 340 万个参数。我们探索了输入分辨率从 96 到 224、width multiplier 从 0.35 到 1.4 的性能权衡。网络的计算成本范围从 7M 到 585M multiply-adds，模型大小从 1.7M 参数到 6.9M 参数不等。

与 [27] 相比有一个细微的实现差异：对于小于 1 的 multiplier，我们对所有 layer 应用 width multiplier，除了最后一个 convolutional layer。这对于较小模型可以提升性能。

5. Implementation Notes

5.1. Memory efficient inference

倒置残差 bottleneck layers 使得实现特别节省内存成为可能，这对于移动端应用尤为重要。一个标准的高效推理实现（例如使用 TensorFlow [31] 或 Caffe [32]）会构建一个有向无环计算超图 $G$，图中边表示操作，节点表示中间计算的 tensor。计算调度的目标是最小化需要存储在内存中的 tensor 总数。

在最一般的情况下，它会在所有合理的计算顺序 $\Sigma (G)$ 上进行搜索，并选择最小化以下表达式的计算顺序：
$$M(G)=\underset{\pi \in \Sigma (G)}{\min }\underset{i\in \mathrm{1..}n}{\max }\left[\sum _{A\in R(i,\pi ,G)}|A|\right]+\mathrm{size}({\pi }_i)$$

其中 $R(i,\pi ,G)$ 表示与任意 ${\pi }_i\dots {\pi }_n$ 节点相连的中间 tensor 列表，$|A|$ 表示 tensor $A$ 的大小，而 $\text{size}(i)$ 是操作 $i$ 在计算过程中所需的全部内存量。

对于只有简单并行结构（如 residual connection）的图而言，仅存在一个非平凡的可行计算顺序，因此对计算图 $G$ 推理所需内存的总量及上界可以简化为：

$$M(G)=\underset{op\in G}{\max }\left[\sum _{A\in {\mathfrak{op}}_{inp}}|A|+\sum _{B\in {\mathfrak{op}}_{out}}|B|+|op|\right](2)$$

换句话说，所需的内存量只是所有操作的输入和输出 tensor 大小的最大总和。接下来我们将展示，如果将一个 bottleneck residual block 视为一个单一操作（并将其中的中间卷积 tensor 视为可丢弃），则内存占用的主要来源将是 bottleneck tensor 的大小，而不是 bottleneck 内部更大的中间 tensor。

Bottleneck Residual Block
如图 3b 所示，一个 bottleneck block 操作符 $\mathcal{F}(x)$ 可以表示为三个操作符的组合：

$$\mathcal{F}(\mathbf{x})=[A\circ \mathcal{N}\circ B]\mathbf{x}$$

其中，$A$ 是一个线性变换：

$$A:{\mathbb{R}}^{s\times s\times k}\to {\mathbb{R}}^{s\times s\times n}$$

$\mathcal{N}$ 是一个逐通道的非线性变换：

$$\mathcal{N}:{\mathcal{R}}^{s\times s\times n}\to {\mathcal{R}}^{s^{\prime }\times s^{\prime }\times n}$$

$B$ 是输出域上的线性变换：

$$\mathbf{B}:{\mathcal{R}}^{s^{\prime }\times s^{\prime }\times n}\to {\mathbb{R}}^{s^{\prime }\times s^{\prime }\times k^{\prime }}$$

在我们的网络中，$\mathcal{N}=ReLU6\circ \mathrm{dwise}\circ ReLU6$，但上述分析适用于任何逐通道的非线性变换。假设输入域的大小为 $|x|$，输出域的大小为 $|y|$，则计算 $F(X)$ 所需的内存最小可达：

$$|s^{2}k|+|s^{\prime 2}{k}^{\prime }|+O(\max (s^2,s^{\prime 2}))$$
算法基于这样的事实：内层 tensor $Z$ 可以表示为 $t$ 个大小为 $n/t$ 的 tensor 的连接，我们的函数可以表示为：

通过累积求和，我们只需要始终在内存中保留一个大小为 $n/t$ 的中间块。使用 $n=t$ 时，我们最终只需始终保留一个通道的中间表示。使我们能够使用这个技巧的两个约束条件是： (a) 内部变换（包括非线性变换和深度卷积）是逐通道的；(b) 连续的非逐通道操作具有较大的输入大小与输出大小的比例。对于大多数传统神经网络，这种技巧不会产生显著的改进。

我们注意到，使用 $t$ 分割计算 $F(X)$ 所需的乘加操作数与 $t$ 无关，然而在现有实现中，我们发现将一个矩阵乘法替换为多个较小的矩阵乘法会由于缓存未命中增加而影响运行时性能。我们发现，这种方法在 $t$ 是一个介于 2 到 5 之间的小常数时最有帮助。它显著减少了内存需求，但仍然允许利用深度学习框架提供的高度优化的矩阵乘法和卷积操作所带来的效率。仍然需要观察是否通过框架层级的特殊优化可以进一步提高运行时性能。

6. 实验

6.1. ImageNet 分类

训练设置 我们使用 TensorFlow[31] 训练我们的模型。我们使用标准的 RMSPropOptimizer，衰减和动量都设置为 0.9。我们在每一层之后使用批归一化，标准的权重衰减设置为 0.00004。按照 MobileNetV1[27] 的设置，我们使用初始学习率 0.045，并且每个 epoch 的学习率衰减率为 0.98。我们使用 16 个 GPU 异步工作者，批次大小为 96。

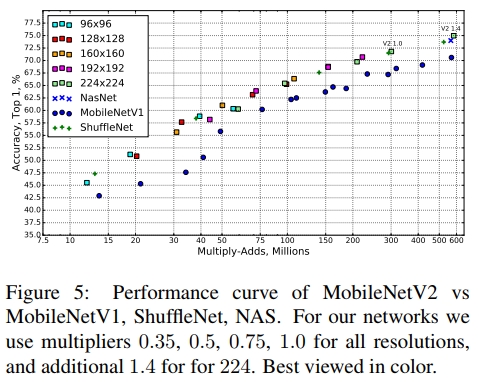
结果 我们将我们的网络与 MobileNetV1、ShuffleNet 和 NASNet-A 模型进行比较。几种选定模型的统计数据见表 4，完整的性能图见图 5。

6.2. 目标检测

我们评估并比较了 MobileNetV2 和 MobileNetV1 作为特征提取器[33] 在 COCO 数据集[2] 上使用修改版单次检测器（SSD）[34] 进行目标检测的表现。我们还与 YOLOv2 [35] 和原始 SSD（以 VGG-16 [6] 作为基础网络）作为基准进行比较。我们没有与其他架构如 Faster-RCNN [36] 和 RFCN [37] 进行比较，因为我们的重点是移动/实时模型。

SSDLite 在本文中，我们介绍了常规 SSD 的一个适合移动端的变种。我们将 SSD 预测层中的所有常规卷积替换为可分离卷积（深度卷积后接 1 × 1 投影）。这一设计符合 MobileNets 的整体设计，且在计算效率上大大提高。我们将这个修改版称为 SSDLite。与常规 SSD 相比，SSDLite 显著减少了参数数量和计算成本，如表 5 所示。

对于 MobileNetV1，我们遵循[33]中的设置。对于 MobileNetV2，SSDLite 的第一层连接到第 15 层的扩展（输出步幅为 16）。第二层及其余 SSDLite 层连接到最后一层（输出步幅为 32）。这一设置与 MobileNetV1 一致，因为所有层都连接到具有相同输出步幅的特征图。

MobileNet 模型的训练与评估

这两个 MobileNet 模型都使用开源的 TensorFlow 目标检测 API[38] 进行训练和评估。两者的输入分辨率为 320 × 320。我们对比了 mAP（COCO 挑战指标）、参数数量和乘加操作数（Multiply-Adds）。结果如表 6 所示。MobileNetV2 SSDLite 不仅是最有效的模型，也是三者中最精确的。值得注意的是，MobileNetV2 SSDLite 在 COCO 数据集上的效率是 YOLOv2 的 20 倍，模型大小则是其 10 倍小。

6.3. 语义分割

在本节中，我们将 MobileNetV1 和 MobileNetV2 作为特征提取器，与 DeepLabv3[39] 一起用于移动设备上的语义分割任务进行比较。DeepLabv3 采用了空洞卷积（atrous convolution）[40, 41, 42]，这是一种强大的工具，用于显式控制计算特征图的分辨率，并构建了五个并行的分支，其中包括：(a) 空洞空间金字塔池化模块（ASPP）[43]，包含三个具有不同空洞率的 3 × 3 卷积，(b) 1 × 1 卷积分支，以及 © 图像级特征[44]。我们用输出步幅（output stride）表示输入图像的空间分辨率与最终输出分辨率的比例，输出步幅是通过适当应用空洞卷积来控制的。对于语义分割，通常使用输出步幅 = 16 或 8 以获得更密集的特征图。我们在 PASCAL VOC 2012 数据集[3] 上进行了实验，使用了来自[45]的额外标注图像，并以 mIOU 为评估指标。

为了构建一个适合移动设备的模型，我们实验了三种设计变化：(1) 不同的特征提取器，(2) 简化 DeepLabv3 分支以加速计算，(3) 不同的推理策略以提升性能。我们的结果总结在表 7 中。我们观察到：(a) 推理策略，包括多尺度输入和加入左右翻转图像，显著增加了 MAdds，因此不适合在设备上应用，(b) 使用输出步幅 = 16 比使用输出步幅 = 8 更高效，© MobileNetV1 已经是一个强大的特征提取器，只需要比 ResNet-101[8] 少约 4.9 - 5.7 倍的 MAdds（例如，mIOU：78.56 vs 82.70，MAdds：941.9B vs 4870.6B），(d) 在 MobileNetV2 的倒数第二个特征图上构建 DeepLabv3 分支比在原始的最后一层特征图上构建更高效，因为倒数第二个特征图包含 320 个通道而不是 1280 个，通过这种方式，我们能达到相似的性能，但需要的操作数比 MobileNetV1 少约 2.5 倍，(e) DeepLabv3 分支计算开销较大，去除 ASPP 模块显著减少了 MAdds，且性能仅有轻微下降。在表 7 的最后，我们识别了一个适合移动设备应用的潜在候选模型（加粗显示），它能达到 75.32% 的 mIOU，并且只需要 2.75B MAdds。

6.4. 消融实验

反向残差连接。残差连接的重要性已经被广泛研究[8, 30, 46]。本文报告的新结果是，连接瓶颈层的快捷连接比连接扩展层的快捷连接表现更好（比较见图 6b）。

线性瓶颈的重要性。线性瓶颈模型在功能上严格弱于具有非线性的模型，因为激活函数总是可以在适当调整偏置和缩放的情况下操作于线性区间。然而，我们在图 6a 中的实验表明，线性瓶颈能够提高性能，支持了非线性在低维空间中破坏信息的观点。

7. 结论与未来工作

我们描述了一种非常简单的网络架构，使我们能够构建一系列高效的移动模型。我们的基本构建单元具有几个特性，使其特别适合于移动应用。它允许非常高效的内存推理，并利用所有神经网络框架中都存在的标准操作。

在ImageNet数据集上，我们的架构在广泛的性能点上提高了现有技术的水平。

在目标检测任务中，我们的网络在COCO数据集上超越了现有的实时检测器，在精度和模型复杂度方面均表现更好。值得注意的是，我们的架构结合SSDLite检测模块，比YOLOv2计算量少20倍，参数量少10倍。

在理论方面：所提出的卷积块具有一个独特的特性，允许将网络的表达能力（由扩展层编码）与其容量（由瓶颈输入编码）分离。探索这一点是未来研究的重要方向。

论文名称：
MobileNetV2: Inverted Residuals and Linear Bottlenecks
论文地址：https://openaccess.thecvf.com/content_cvpr_2018/papers/Sandler_MobileNetV2_Inverted_Residuals_CVPR_2018_paper.pdf