S参数的含义
S参数的含义:
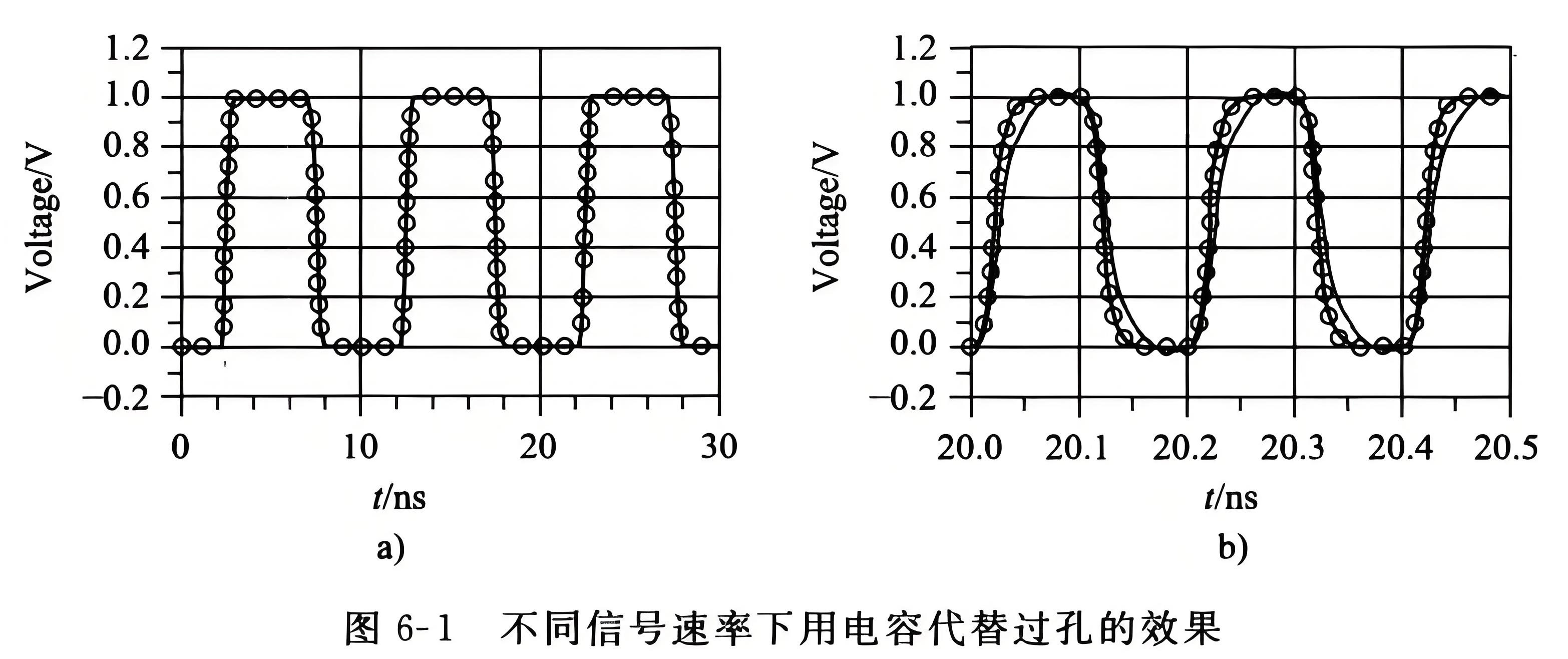
在低速设计时代,工程界普遍使用等效集总电路模型来描述互连通道的过孔、连接器等各部分。对于上升时间达到几个ns的低速数字信号,甚至可以使用一个0Ω电阻代替连接器,分析的结果也不会和实际情况有太大的差别。但是当传输速率达到GHz以上时,这种使用集总电路模型的等效方法就会和实际情况偏离较大。使用一个小电容来代替过孔是另外一种常见的近似,对于上升时间达到几个ns的低速数字信号,这种近似能够很好地模拟过孔的行为,图6-1a显示了这种近似对信号波形的模拟几乎没有偏差。但是对于边沿非常陡峭的高速信号,这种近似的误差是不可忍受的,图6-1b中信号为10GHz,上升时间为30 ps,使用电容近似明显偏离过孔的实际特性。因此,随着信号速率的提高,需要新的模型来表示互连线中的各种结构。
S参数作为描述线性无源互连结构的一种行为模型,来源于网络分析方法。这种模型不考虑互连结构的具体形式,把互连结构当成“黑盒子”,仅仅通过在端口处的参量就能完全描述互连结构的全部行为特征,在高频领域得到非常广泛的应用。在SI领域,由于信号速率的提高,常常需要考虑到几十个GHz范围内的频率成分,因此S参数已成为信号完整性分析与设计中必不可少的重要工具。
本章并非是对S参数严谨的数学说明,而是基于信号完整性的设计,从使用S参数的角度出发,提供一些观察与分析的方法,以帮助读者更直观地理解S参数。
网络分析基础:
网络分析方法是一种频域方法,在一组离散频率点上,通过在输入和输出端口得到的参量完全描述线性时不变系统,无需了解系统内部的详细结构,把目标对象当作黑匣子来处理。在进行网络分析时,关注的是端口处的激励和响应之间的关系。例如,一个二端口网络具有两个端口,如果这个网络是线性的,那么在任何一个频率点该网络的“行为”都可以由两个等式来完全描述。首先我们来看使用阻抗参数如何描述该网络。二端口网络如图6-2所示,
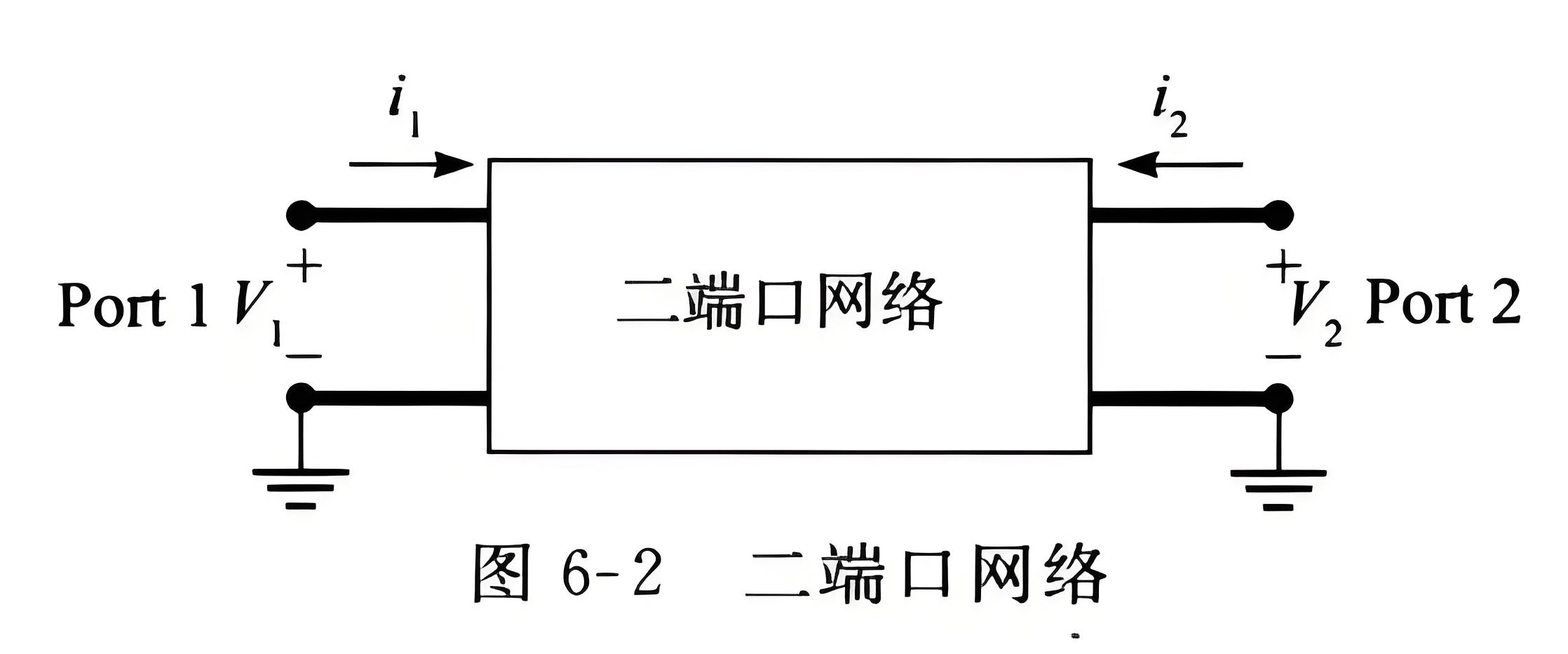
该网络可用下面两个等式来描述

![]()
如果、
、
、
、4个参量已知,那么根据施加的激励,就可以得到响应。如果端口1存在电流激励源
,那么端口1和端口2的响应(电压)都可以得到,V₁=
*
, V₂=
*
。
因此该网络的特性完全可以由4个阻抗参量来确定。在低频段,这4个阻抗参量可以在端口处测得,端口2在开路的情况下可测得 ,
,
端口1在开路的情况下可测得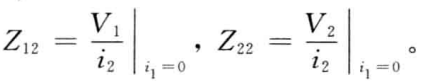
通常用矩阵形式来表示式(6-1),矩阵如下所示。


这样二端口网络就可以有一个阻抗矩阵完全描述:

![]()
用阻抗矩阵来描述二端口网络尽管简单直观,但是在高频时却无法使用。因为阻抗矩阵的4个参量需要在端口处测量得到,测量时需要让其中一个端口完全开路,高频时很难做到完全开路,即使是一个很小的寄生电容也可能会严重影响测量结果的正确性。因此需要使用另外的方式来描述网络,S参数避免了阻抗矩阵测试中的问题,并且测量准确方便,因此得到了广泛的应用。
应该指出的是,阻抗矩阵对分析某些问题非常有用且方便。尽管高频时无法通过测量得到准确的阻抗矩阵,但是如果能够通过其他间接的方法转换得到阻抗矩阵,就能充分发挥阻抗矩阵在分析问题中的作用。
S参数定义:
用S参数来表征线性网络是基于波的传播理论,反映的是信号的入射波与反射波之间的关系。根据波传播方程,端口处的电压可表示为

![]()
假设端口阻抗为, 则端口的电流可表示为:

![]()
因此,如果能够得到端口处的入射信号和反射信号之间的关系,那么也可以完全反映网络的特性。以二端口网络为例,图6-3显示了以入射波和反射波表征网络的方法。定义了4个表征入射波和反射波的参量a₁、b₁、a₂、b₂。


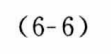
可以使用下面的两个等式表征二端口网络:


其矩阵形式为

![]()
从定义可见,;(i=1,2)表示的是阻抗归一化的入射信号电压,
(i=1,2)表示的是阻抗归一化的反射信号电压,因此
将入射信号和反射信号联系起来。这组参数
,就称为S参数。
如果确定了入射信号和反射信号情况,那么端口处的电压和电流也就确定了。为方便分析,忽略, 电压电流和入射信号及反射信号之间的关系可简写为


入射信号及反射信号也可以使用端口处的电压和电流表示:

![]()
