DAY1:错题日记
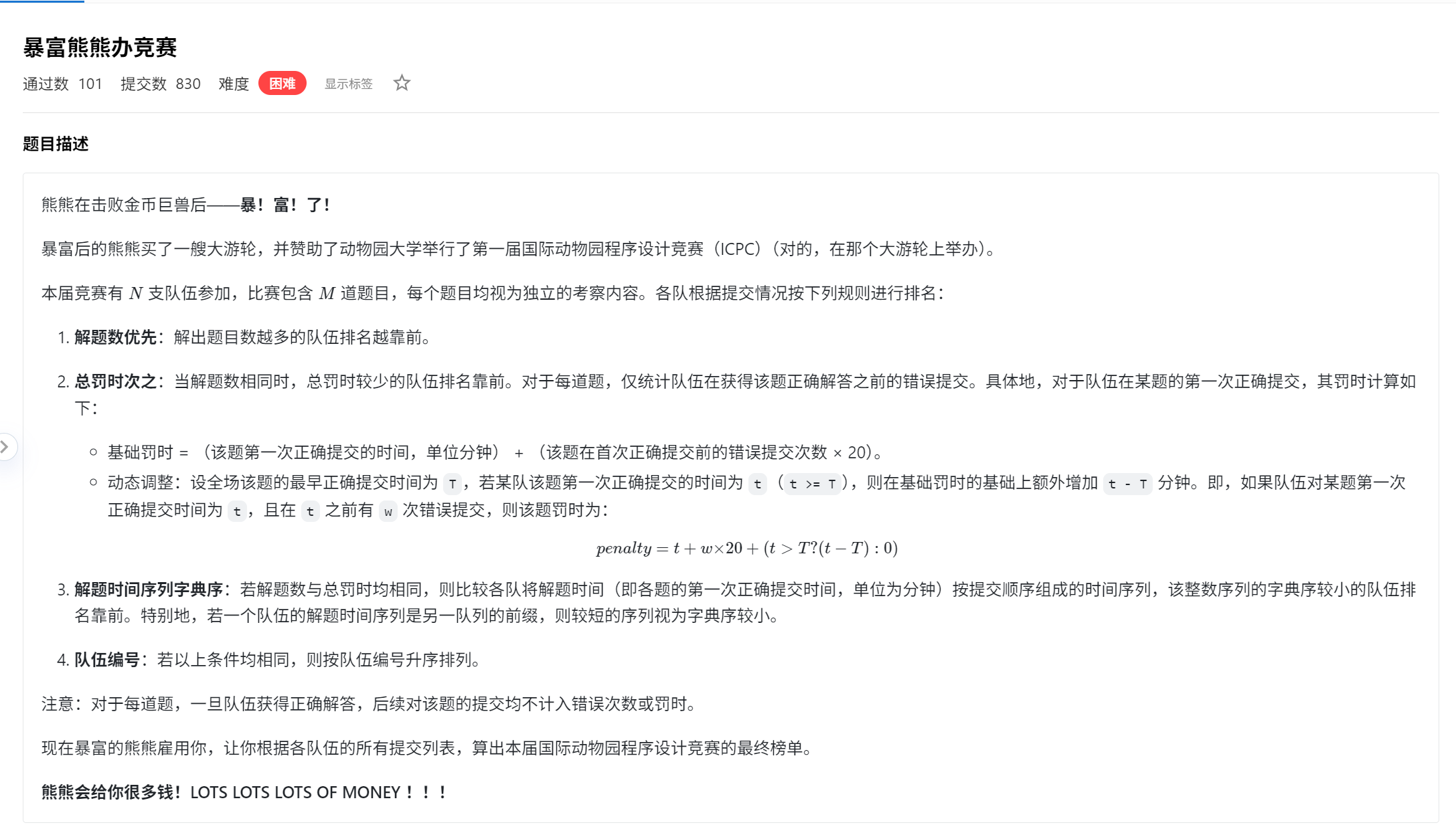
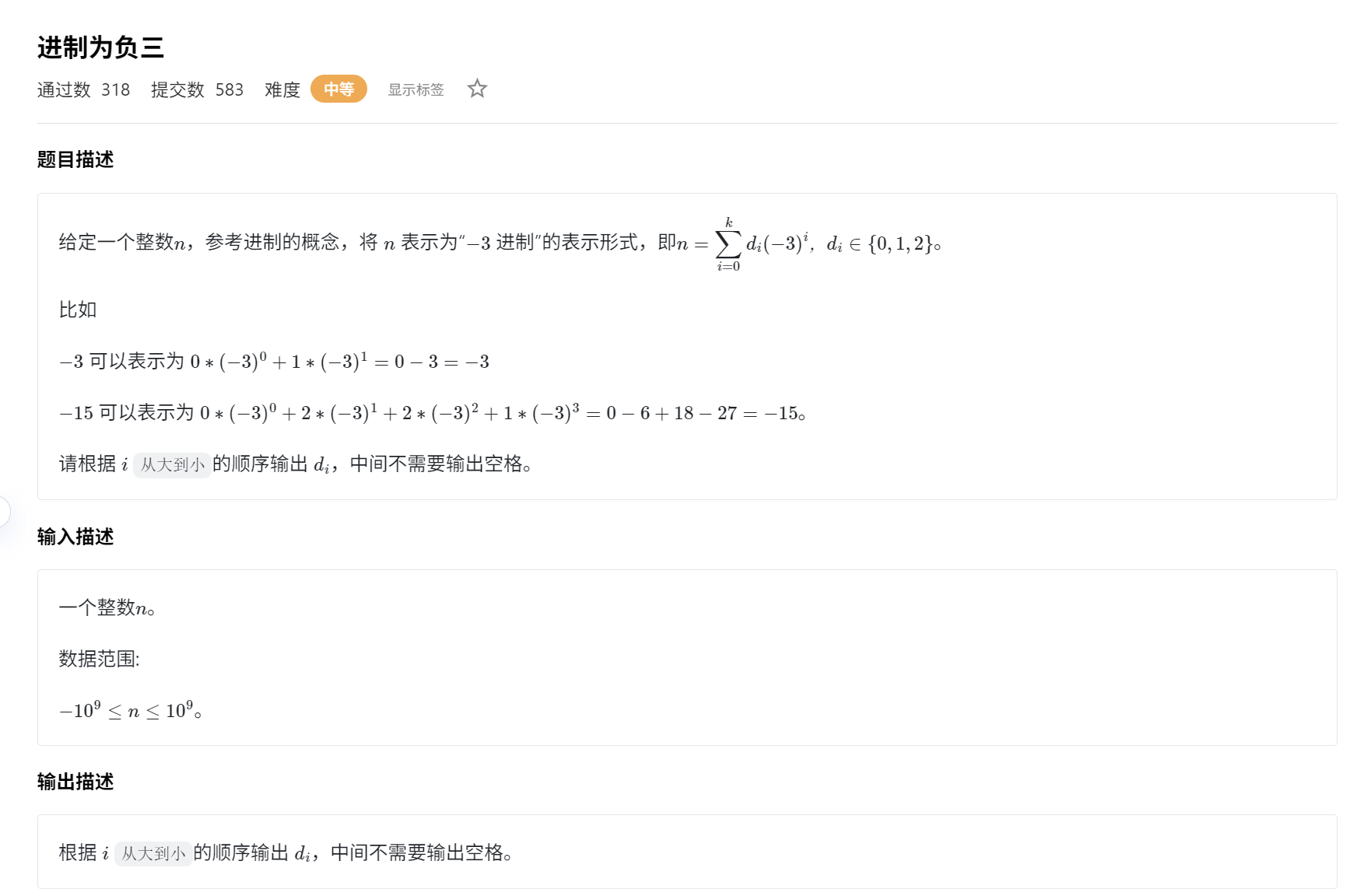
T1:进制为负三
晴问算法-进制为负三
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define pii pair<int,int>
#define f first
#define s second/*我们知道进制转换是“辗转相除倒取余”,对于负进制也是如此,我们用给定数进行辗转相除,但是我们知道负进制可能会出现,余数为负的情况,这是不可取的,我们需要进行一次转换,使得余数变成正假设: 给定整数n,进制为-dn/(-d)=k...r如果r为负数,我们知道n=(-d)*k+r所以为了让r变成正数,可以令 n=(-d)*(k+1)+(r+d);
*/int n;
signed main(){cin>>n;if(n==0){cout<<0;return 0;}int d=-3;string s="";while(n!=0){if(n%d>=0){s+=to_string(n%d);n/=d;}else{//如果余数为负数s+=to_string(n%d-d);n=(n/d)+1; }}reverse(s.begin(),s.end());cout<<s;
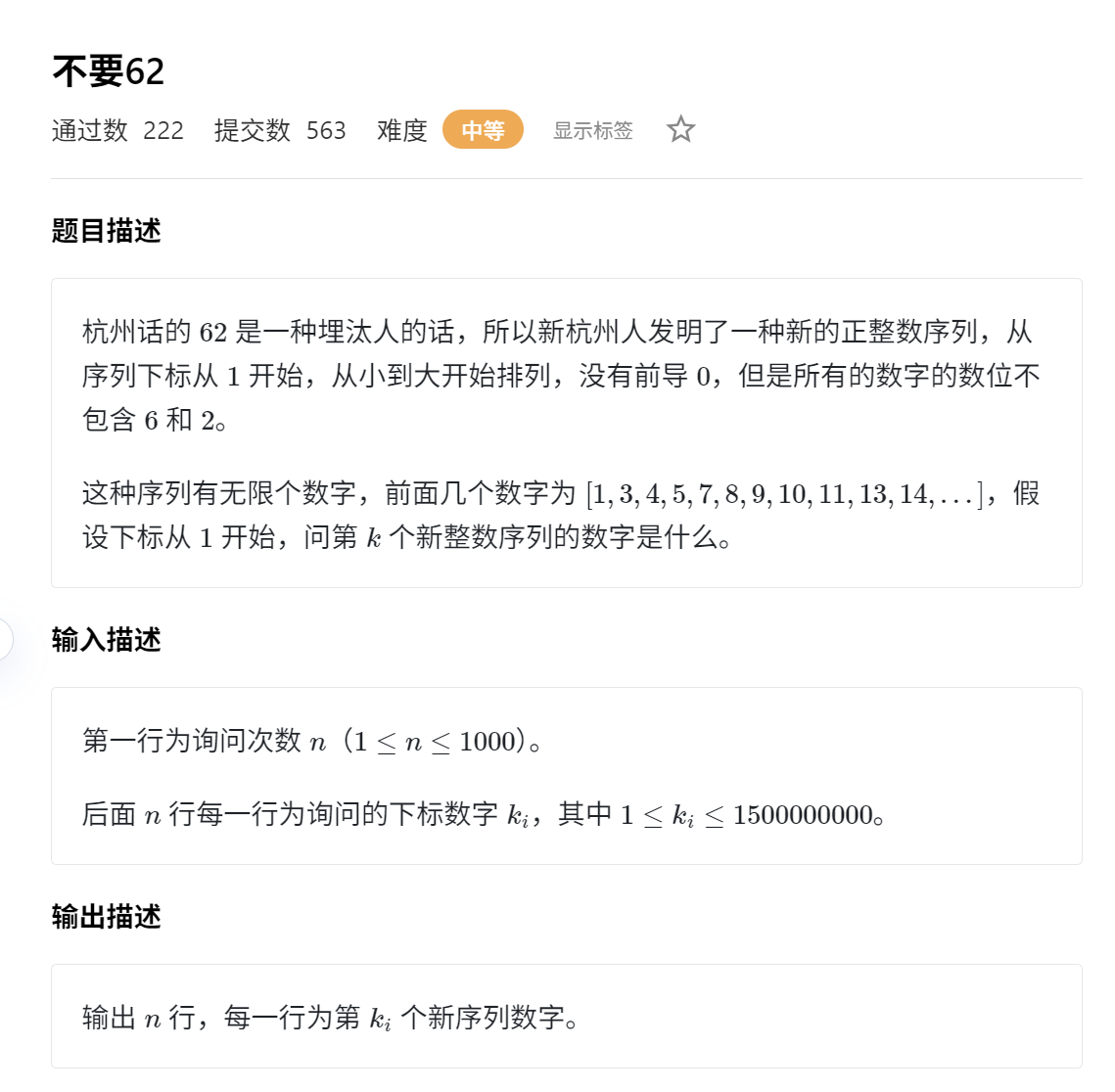
}T2:不要62
晴问算法-不要62
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define pii pair<int,int>
#define f first
#define s second
int n;
//八进制1 3 4 5 7 8 9 0
int a[8]={0,1,3,4,5,7,8,9};
//还是进制转换的模拟,辗转相除逆取余
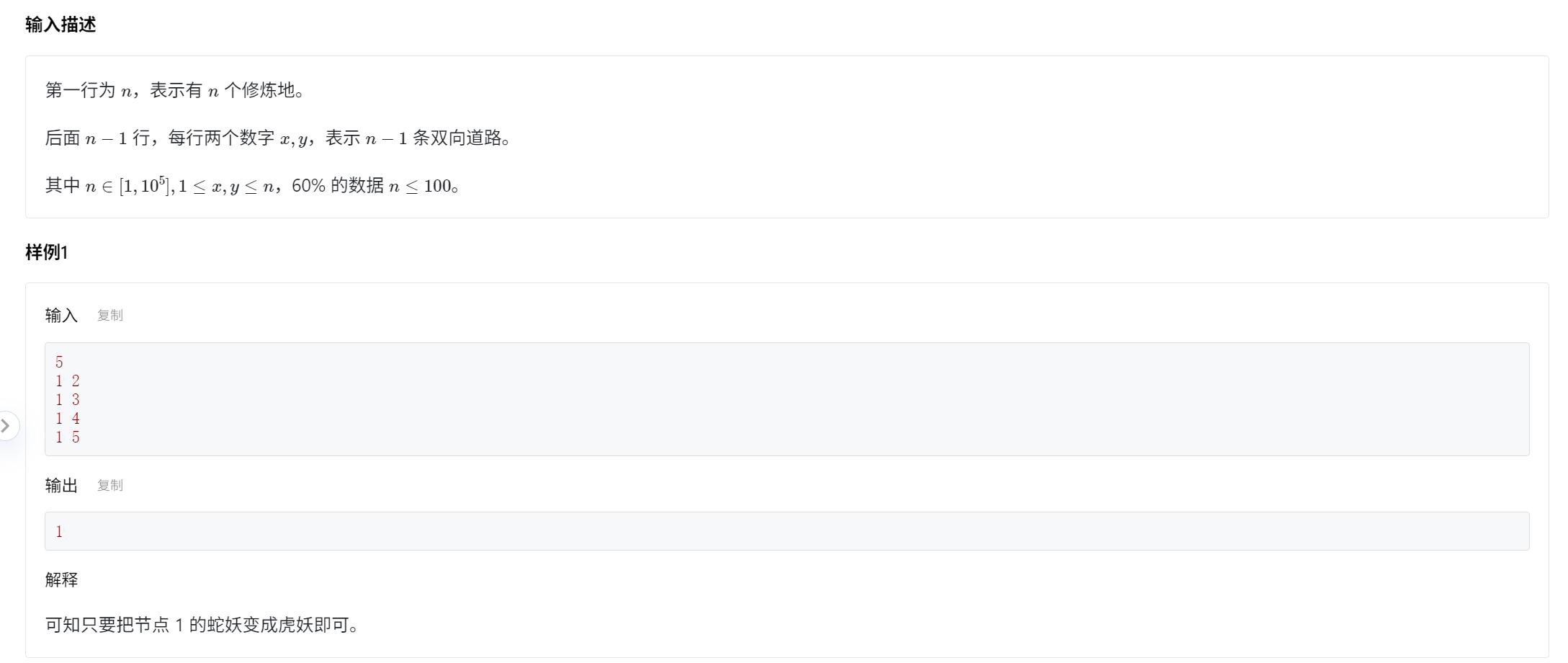
signed main(){int n;cin>>n;while(n--){int k;cin>>k;string s="";while(k){s+=to_string(a[k%8]);k/=8;}reverse(s.begin(),s.end());cout<<s<<endl;}}T3:黄花清修
晴问算法-黄花清修

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define pii pair<int,int>
#define mii map<int,int>
#define f first
#define s second/*思维题:怎么进行转换会使得转换次数最小。我们考虑从正中间位置开始转换,每次转换后相同的点覆盖率向外扩充一圈我们就发现这个覆盖的次数,和树的直径d有关系如果d为偶数,刚好从中间的点开始向外,ans=d/2如果d为奇数,则中间有两个点,从任一一个点开始往外找,都会比一半多1次,即ans=(d+1)/2
*/
int n;
vector<int> g[100010];
bool b[100010];
int pos;//用于记录最深的顶点
int len;//深度
void dfs(int x,int d){ //x是起点,d是深度if(d>len){len=d;pos=x;}for(int y:g[x]){if(!b[y]){b[y]=true;dfs(y,d+1);}}
}
signed main(){cin>>n;for(int i=1;i<n;i++){int x,y;cin>>x>>y;g[x].push_back(y);g[y].push_back(x);}//两次DFS//第一次从任意一点开始找到最深的顶点,即为第一个DFS直径顶点//第二次从找到的最深的顶点开始,找到最深的顶点。长度即为直径db[1]=true;dfs(1,0);memset(b,0,sizeof(b));len=0;dfs(pos,0);cout<<(len+1)/2;
}