数据挖掘 4.1~4.7 机器学习性能评估参数

4.1 Scientific Method
4.1 科学方法
4.2 Why measure performance?
4.2 为什么要衡量绩效？
4.3 Accuracy and its assumptions
4.3 准确率及其假设
4.4 Confusion matrix and associated metrics
4.4 混淆矩阵及其相关指标
4.5 ROC Curves
4.5 ROC 曲线
4.6 PR Curves
4.6 PR 曲线
4.7 PR-ROC Relationship and coding
4.7 PR-ROC 关系及编码

如何评估机器学习模型在特定问题上的表现，被称为评估和对比模型（evaluating and comparing models）。

目标 (Objectives)

如何估计泛化性能，如何仅使用训练数据来估计模型的泛化能力？
如何比较机器学习模型——两个分类器哪个更好？
如何选择机器学习模型的最优参数——如何选择参数 “C” 或 “k”？
评价指标 (Metrics)：Accuracy, FPR, TRP, PPV, ROC, PR-Curves, F-measure
交叉验证与重采样 (Cross-Validation and Resampling)

Evaluation Metrics 评估指标

训练集 (Training Set)：用于训练模型。
测试集 (Test Set)：用于模型性能评估。

项目	Value
训练集 (Training Set)	用于训练模型
测试集 (Test Set)	用于模型性能评估

训练集和测试集必须严格分离，否则会导致数据泄漏，评估不准确。

混淆矩阵（Confusion Matrix）四要素

Condition (True)	Test (Predict)	结果	是否错误
Positive (+)	Positive (+)	TP（true positive） 真阳	Not error
negative (-)	negative (-)	TN（true negative） 真阴	Not error
Positive (+)	negative (-)	FN （false negative） 假阴	Error
negative (-)	Positive (+)	FP（false positive）假阳	Error

名称和预测的保持一致

准确率 Accuracy

二分类任务 (Two-Class Classification)
定义：正确预测的百分比 (Percentage of Correct Predictions)
公式
$$Accuracy=\frac{tp+tn}{tp+tn+fp+fn}$$

假设 (Assumptions)

1. 数据集是 平衡的 (The data set is balanced) （一半一半这非常重要）
2. 任何类别的误分类同样糟糕 (Misclassification of any class is equally bad)
3. 使用的分类 阈值是最优的 (The threshold used for classification is optimal)

满足这些假设条件，准确率是一个很好的评估标准。

数据集平衡的重要性

如果数据集 类别分布极不平衡，那么准确率就可能产生 误导性。
举例
数据集：1000 个样本

• 正类 (+)：50 个
• 负类 (-)：950 个

模型策略：永远预测为负类
预测结果：

• TN = 950
• FN = 50
• TP = 0
• FP = 0

准确率计算
$$Accuracy=\frac{950}{1000}=95\%$$
分析：看似 95% 很高，但实际上模型完全没有学习到识别正类的能力 （模型永远预测为负类） （召回率 Recall = 0）。

阈值 （Threshold）以及分类性能 (Classification Performance)

分类器（或任意机器学习模型）可以看作是一个函数，
$$y=f(x|\theta )$$
给定输入 $x$ 和参数集合 $\theta$，通过决策函数 $f(x|\theta )$ 生成输出 $y$。
分类器的输出通常是一个 实值 (real-valued)，然后通过 阈值 (threshold) 转换为分类标签。
$$\begin{gathered} f(x|\theta )>0\Rightarrow y=+1 \\ f(x|\theta )<0\Rightarrow y=-1 \end{gathered}$$
说明

• 这里 0 作为阈值 (threshold)。
• 标签会随着阈值的选择而变化。
• 准确率是基于二值化的特定阈值计算的，如果阈值设置太高，TP和FP的数量就会改变，从而改变准确率。所以我们一般说，分类器的准确率是通过这个阈值进行参数化的。

题目 1：平衡数据集 (Balanced Dataset)

假设数据集是平衡的（正类与负类样本数相等）。
考虑一个随机分类器，该分类器对输入样本随机输出分数。 问题：它的准确率是多少？
考虑一个恒等分类器，该分类器对所有输入都预测为 +1。 问题：它的准确率是多少？

解答

1. 随机分类器

• 在平衡数据集中，随机预测相当于抛硬币，猜对概率 50%。
• 因此准确率约为 50%。

2. 恒等分类器（总是预测 +1）

• 正类和负类数量相等，预测正类能覆盖一半正确（TP = 一半）。
• 因此准确率也为 50%。

题目 2：不平衡数据集 (Imbalanced Dataset)

假设数据集是 极度不平衡的（负类数量 ≫ 正类数量）。
考虑一个随机分类器，该分类器对输入样本随机输出分数。 问题：它的准确率是多少？
考虑一个恒等分类器，该分类器对所有输入都预测为 +1。问题：它的准确率是多少？

解答

1. 随机分类器

• 虽然数据集不平衡，但纯随机预测正负类的概率各为 50%。
• 长期来看，准确率仍然约为 50%。

2. 恒等分类器（总是预测 +1） 由于 $N\gg P$，准确率会非常低，接近 0%。

混淆矩阵（Confusion Matrix）

混淆矩阵，列是真实阴阳，行是预测阴阳。第一个是positive，第二个是negative。主对角线是预测正确的

可以看出，
各项指标Sensitivity 敏感度、Specificity 特异性、Precision 精确度都是 T开头，在它所属行或者列的占比。可见，预测正确是我们唯一关心的。

Sensitivity 敏感度（又名 recall，TPR）

$$Sensitivity=\frac{TP}{TP+FN}$$
在所有真的positive中，被预测正确的占比，是sensitivity。

Specificity 特异性

$$Specificity=\frac{TN}{TN+FP}$$
在所有真的negative中，被预测正确的占比，是specificity。

Precision 精确度

$$Precision=\frac{TP}{TP+FP}$$
在所有预测positive中，被预测正确的占比，是precision。

F 指标（F1-score）

F1 分数是 精确率 (Precision) 和 召回率 (Recall) 的调和平均数，是整个混淆矩阵的汇总统计数据：

$$F=2\times \frac{precision\times recall}{precision+recall}$$

混淆矩阵高级版

ROC曲线

TPR 与 FPR 定义
真阳率 (True Positive Rate, TPR) ：

$$TPR=\frac{TP}{TP+FN}$$

$TPR(t)=P(f(x)>t|y=1)$ ， 表示：分类器在 正类样本 (y=1) 中，分数高于阈值 $t$ 的概率。

假正率 (False Positive Rate, FPR)：
$$FPR=\frac{FP}{FP+TN}$$

$FPR(t)=P(f(x)>t|y=-1)$ ， 表示：分类器在 负类样本 (y=-1) 中，分数高于阈值 $t$ 的概率。

通过改变阈值（threshold），针对给定测试集计算出的FPR和TPR。我们得出FPR和TPR曲线，在不考虑阈值的情况下，我们得出ROC曲线。

上图是误差率与阈值的曲线。

ROC曲线是单调不减的（monotonically non-decreasing）

AUC-ROC(the area under the ROC curve)ROC曲线下面积

ROC曲线下面积（缩写为AUC-ROC）可以作为性能指标，与分类器的阈值无关。如果你想摆脱阈值，希望分析分类器在所有阈值范围内的性能，可以直接计算AUC-ROC 即ROC曲面下面积。该数值越高或越接近1，分类器性能就越好。

下图是理想的ROC曲线，AUC-ROC=1

ROC问题思考

1. 一个完美分类器的 ROC 曲线会是什么样子？
   如上图

2. 一个随机分类器的 ROC 曲线会是什么样子？
   

3. 一个总是预测为正类的分类器的 ROC 曲线会是什么样子？
   

4. ROC 曲线的基本假设是什么？

假设 (Assumptions)
数据集是 平衡的 (The data set is balanced) （正的一半负的一半这非常重要）
任何类别的误分类同样糟糕 (Misclassification of any class is equally bad)
使用的分类 阈值是最优的 (The threshold used for classification is optimal)
满足这些假设条件，准确率是一个很好的评估标准。

上述是准确率的前提要求，因为ROC和阈值无关，是所有阈值下的性能表现。所以没有第三条，前两条都是符合的。

5. ROC 曲线的哪一部分是最重要的？
   取决于应用，某些情况下，我们希望FPR非常低，真阳率很高。这个情况与类别的不平衡率有关。

等错误率 equal error rate

$$TPR+FPR=1$$

PR 曲线

Precision 和 Recall的图

$$Precision=\frac{TP}{TP+FP}$$
$$Sensitivity=recall=\frac{TP}{TP+FN}$$

如果我们需要从大量负样本中检测出少量类（大海捞针），应该使用准确率作为性能指标。

在类别不平衡或需要精确度（precision）的情况下很有用。
PR 曲线与ROC曲线不同，ROC曲线是单调递增的，PR曲线不是单调的，是随着阈值的变化而上下波动（因为精确度会随着阈值上下波动）。

我们知道AUC-ROC在随机分类器中，图像是主对角线。但对于PR图像，不是这样，随机分类器的PR曲线下面积取决于有多少个负类，会随着测试机中有多少个负例而变化。如果负例的数量是随机的，那PR-AUC总是接近0.5。

示例

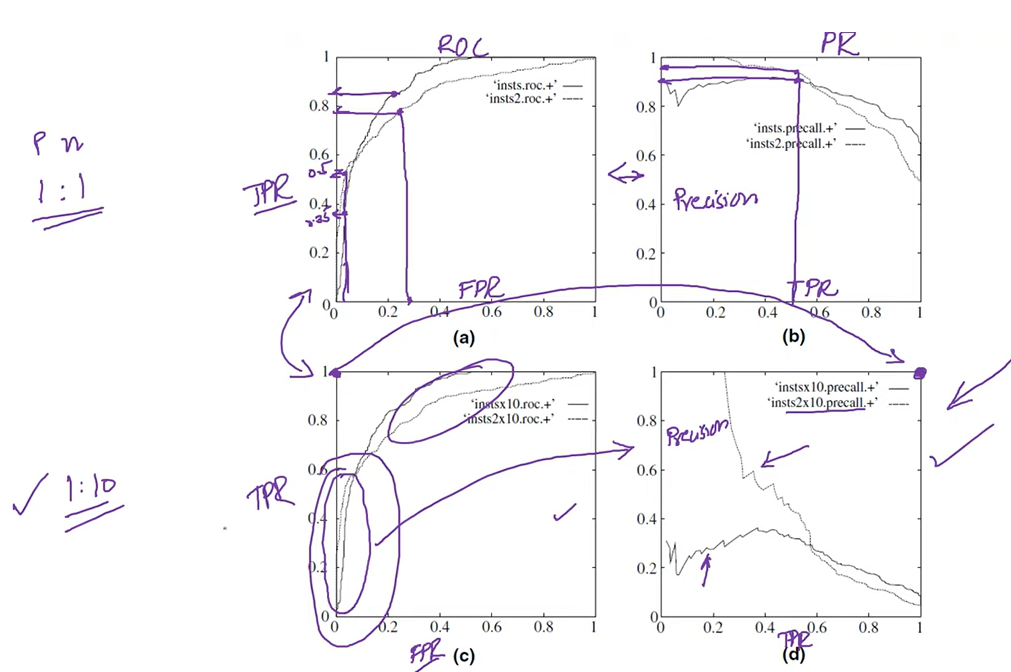
1 第一行是平衡的数据，正负比例1：1。第二行是不平衡的数据，正负比例1：10。可以观察出ROC图像没有受任何影响，说明对平衡无感受。但PR图像变化巨大，说明对平衡敏感；
2
$ROC的y轴=PR的x轴=TPR$
3 除了FPR，剩下的参数都是越大，性能越好；
4 ROC最重要的是前后两部分；
5 第二行图像最理想的点画出来了，都是性能最理想最好的点。

ROC 与 PR 曲线的关系

ROC 曲线与 PR 曲线之间存在一一对应关系 (One-to-One correspondence between the two curves)

• 如果一条曲线在 ROC 空间中占优，那么它在 PR 空间中也占优
  (If a curve dominates in ROC space then it dominates in PR space.)

• 如果一条曲线在 PR 空间中占优，那么它在 ROC 空间中也占优
  (If a curve dominates in PR space then it dominates in ROC space.)

随机分类器的 PR 曲线是什么样的？ (What will be the PR curve for a random classifier?)
答：
我们知道随机分类的ROC曲线是一个对角线。但PR曲线不是。

PR曲线会根据负例的数量得到不同的曲线。所以，随机分类器的面积，也就是PR下的面积不会是0.5，这取决于有多少个负例。

ROC 曲线的哪一部分对 PR 曲线影响更大？ (What part of an ROC curve impacts the PR curve more?)
左下部分